[백준] N과M(2) (JAVA)

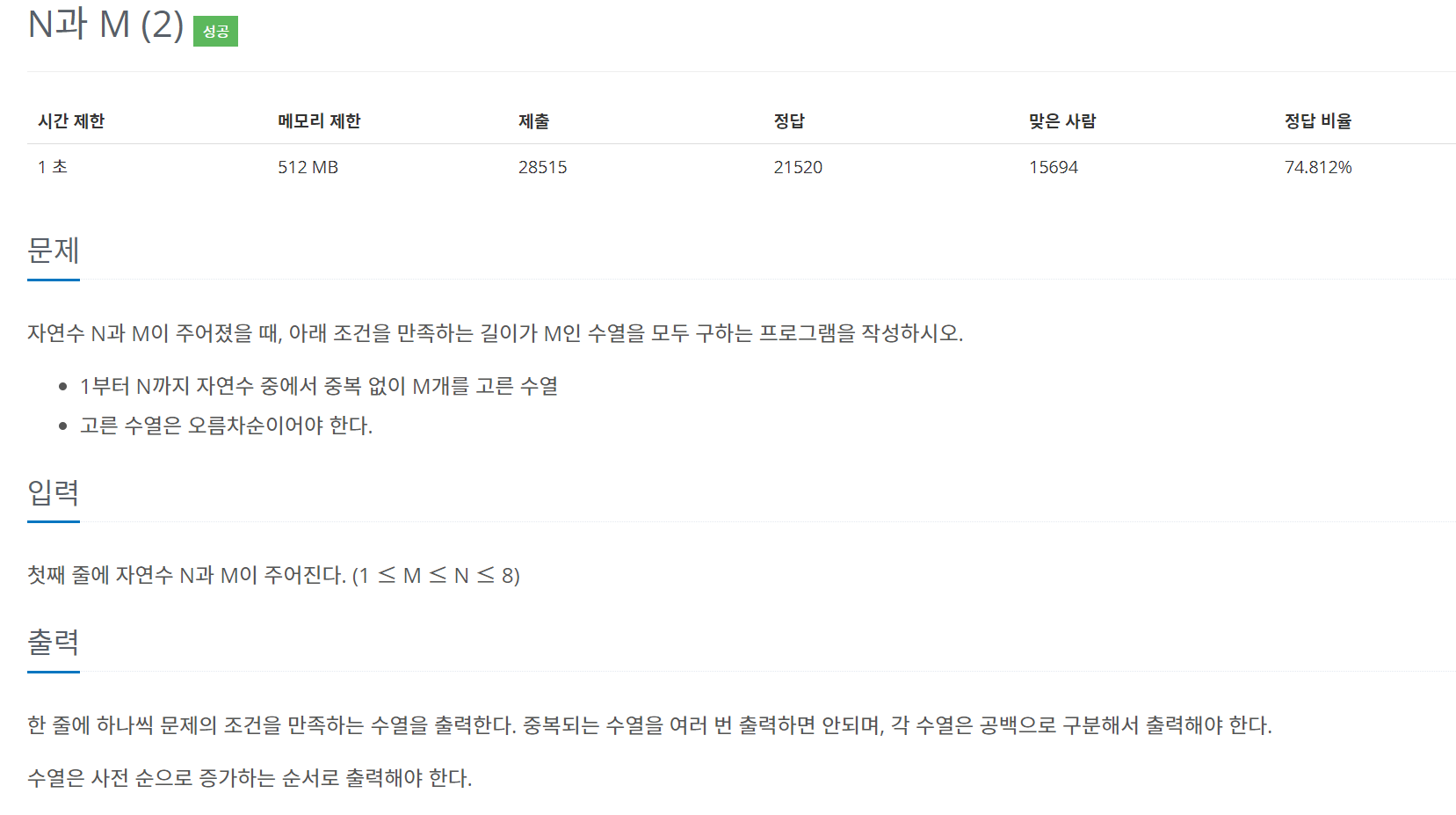
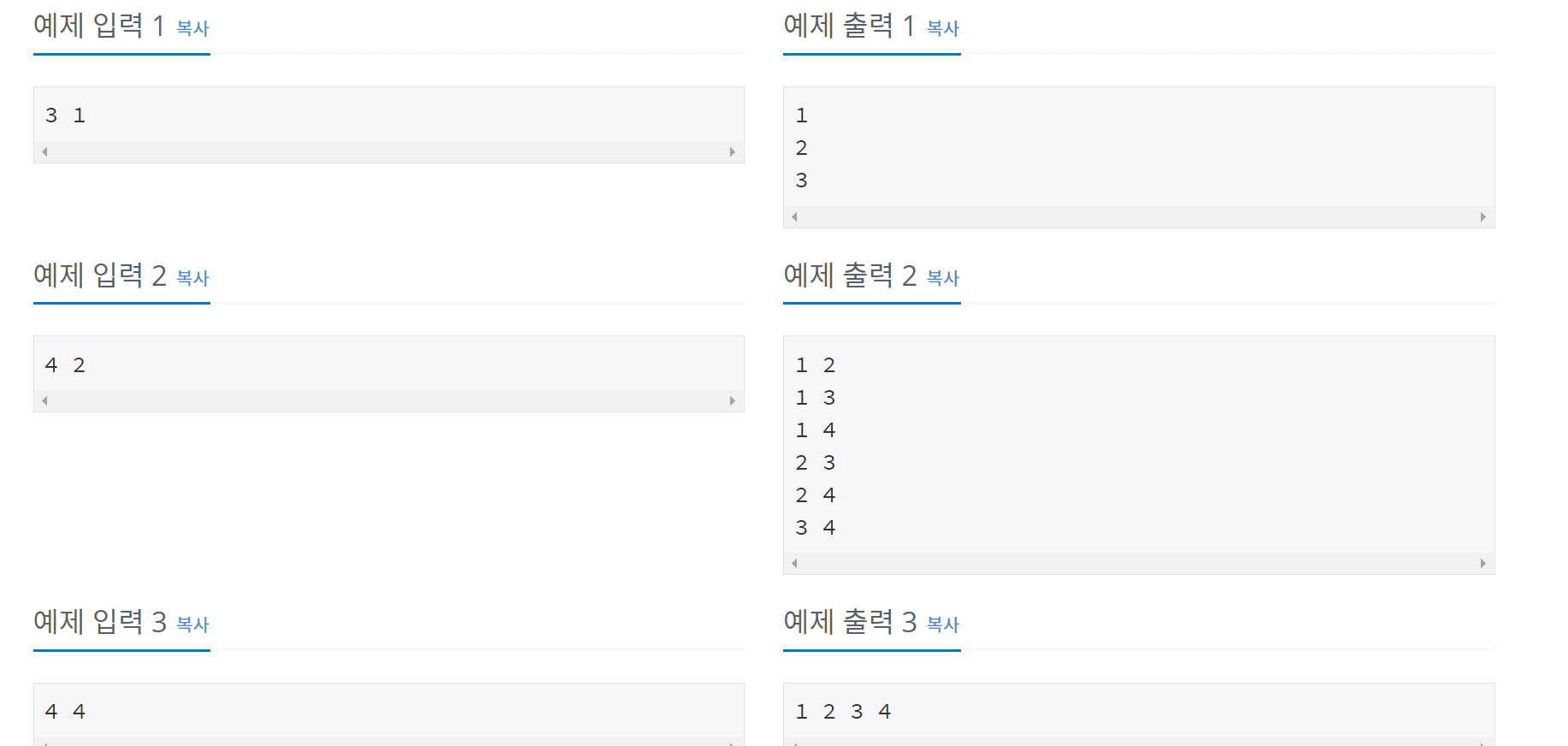
N과M (1)은 순열(Permutation)을 이용하는 문제였고 (2)번은 조합(Combination)을 이용하는 문제이다.
단순히 nCr의 조합의 갯수를 구하는 것이 아니라 각각의 경우의수를 모두 구해야해서 까다롭다.

nCr = n-1Cr-1 + n-1Cr

위와 같은 조합의 성질을 이용하여 문제를 풀어나가도록 하겠다.

예를들어 {1,2,3,4} 중에 2개를 뽑는 4C2라면, 우선 1을 뽑는경우와 1을 뽑지않는 경우로 나뉠수 있다. 1을 뽑는 경우라면 나머지 {2,3,4}중에 하나만 뽑으면 되므로 3C1이 된다. 또, 1을 뽑지 않는 경우라면 나머지 3개에서 2개를 뽑아야하므로 3C2가 된다.
따라서 4C2 = 3C1 + 3C2이다. 즉, 1을 뽑는경우 + 1을 뽑지않는 경우이다.

target : output 배열에 넣을 값
index: output 배열의 인덱스

import java.io.*;

public class No15650_N과M_2 {
    static int output[];
    public static void main(String[] args) throws IOException{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        String temp[] = br.readLine().split(" ");
        int N = Integer.parseInt(temp[0]);
        int M = Integer.parseInt(temp[1]);

        output = new int[M];

        combination(N,M, 1,0);
    }

    static void combination (int n, int r, int target,int index) {
        if (r==0){ //r값을 하나씩 줄여서 0이되면 r개를 다 뽑았다는 뜻
            for(int i =0 ; i < index; i++) {
                System.out.print(output[i]+" ");
            }
            System.out.println();
        }

        else if(target ==n+1) //끝까지 모두 탐색함
            return ;
        else {
            output[index] = target;
            combination(n, r - 1, target + 1, index + 1); //현재 타겟을 뽑음
            //뽑았으므로 r값 감소, target은 항상 1씩증가, 뽑았으므로 index증가
            combination(n, r, target + 1, index); //현재 타켓을 안뽑음
            //안뽑았으므로 r이 감소하지않음, target은 항상 1씩 증가, 안뽑았으므로 index그대로 
        }
        }
    }