[알고리즘] 그래프(Graph) ,인접행렬과 인접리스트

그래프

그래프란 Vertex(정점)과 Edge(간선)으로 이루어진 자료구조이다. 정점과 정점사이의 관계를 간선으로 표현한다.

G=(V,E) 로 표현하며 G(5,6)이면 정점이 5개이고 간선이 6개인 그래프이다.
예를들어 이런 모양이 될 수 있다.

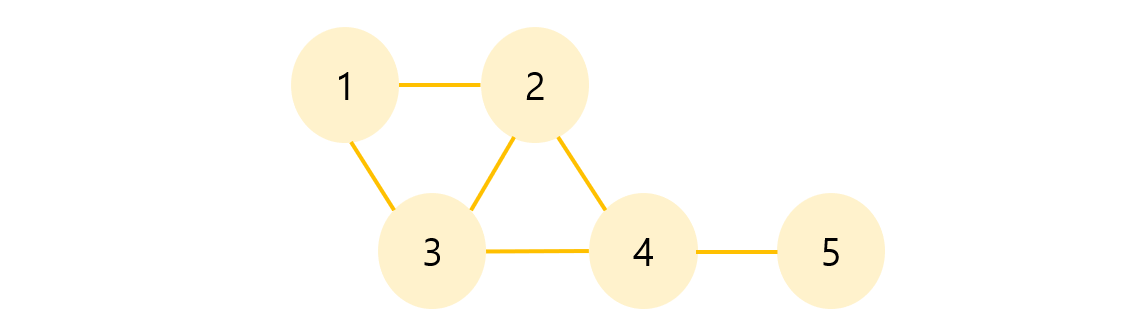
• 그래프는 간선의 방향유무에 따라 방향 그래프와 무방향 그래프로 나뉘어지는데, 방향 그래프일 경우에는 화살표를 그려 어느vertex로 향하는지를 나타내주고, 무방향일 경우에는 화살표를 생략하고 실선으로 표현한다.
  무방향일 경우에는 1->2로 가는 간선과 2->1로 가는 간선이 동일하다고 간주한다.

• 가중 그래프 : 간선에 가중치가 부여된 그래프

• 경로 (Path) : 정점 A에서부터 정점 B까지의 길
  예를 들어 위의 그래프에서 정점1부터 정점4까지의 경로는

  1->2->4
  1->3->4
  1->2->3->4
  1->3->2->4

  가 있다.
  

• 사이클 (Cycle) : 출발점과 도착점이 같은 경로
  예를 들어 위의 그래프에서 사이클은

  1->2->3->1
  2->3->4->2

등이 있다.

그래프 구현

그래프는 두가지 방법으로 구현할 수 있다.

1. 인접리스트

2. 인접행렬

인접리스트는 연결리스트를 이용하여 구현하는 방법이고 인접행렬은 이차원배열(행렬)을 이용하여 구현하는 방법이다.

인접리스트 구현

연결리스트를 이용하여 각 정점과 인접한 다른 정점들을 저장하는 방법이다. 그림을 통하여 이해하면

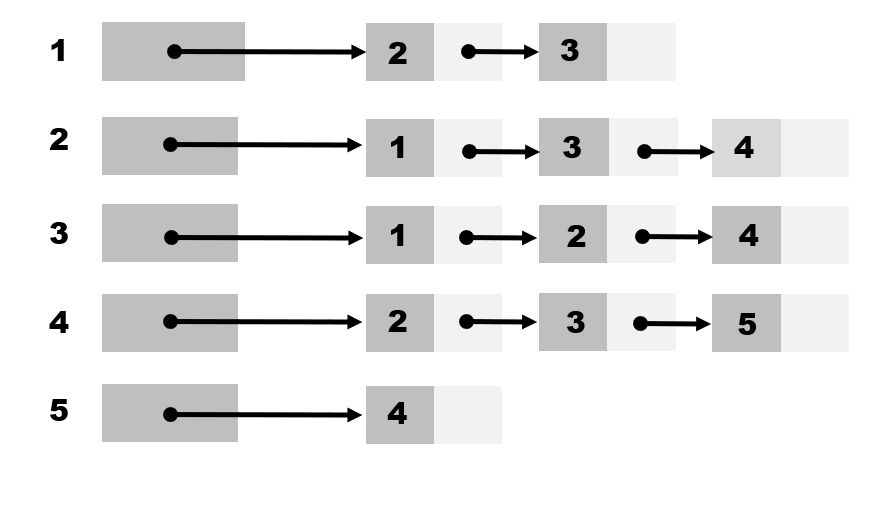
위와 같이 정점1에 연결된 정점은 2와 3이 있고,
정점2에 연결된 정점은 1,3,4가 있다. 3,4,5도 마찬가지 방식으로 연결되어 있는 정점들을 표시하는 것이 인접리스트 방식이다.

인접행렬 구현

행렬(2차원 배열)을 사용하여 구현하는 방법으로, n개의 정점이 있을 때 nXn 크기의 행렬을 만든다. 각 정점에 대해 인접한 정점이 있다면 행렬의 원소를 1로 표시한다. (인접하지 않다면 0으로 표시)

계속 위의 예시를 가지고 설명하자면, 지금 1은 2와 인접해있고, 3과도 인접해있다. 하지만 1은 4,5와는 인접해있지 않다.그렇다면 (1,2) ,(1,3)은 1이고 (1,4), (1,5)는 0이다.

또, 방향이 없는 그래프이므로 행과 열이 뒤집힌 (2,1), (3,1)역시 1이고 (4,1),(5,1)은 0이다. 따라서 무방향 그래프에서는 (n,n)을 기준으로 행렬이 대칭을 이룬다.

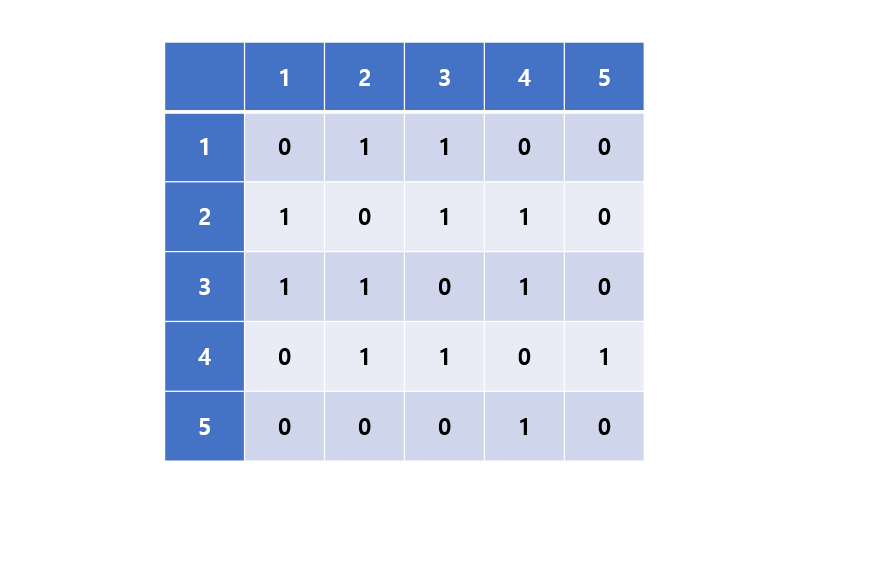
인접행렬을 이용하여 그래프를 구현하는 경우 간선의 수에 상관없이 항상 n^2만큼의 메모리 공간이 필요하다. 따라서 간선이 적은 그래프를 인접행렬로 표현하면 메모리가 많이 낭비 된다.

인접리스트 VS 인접행렬

• 인접리스트는 정점간의 인접여부를 알기 위해 순차 탐색을 해야하므로 간선이 적은 희소그래프를 구현할 때 적합하다. 그리고 정점과 간선의 삽입과 빠르며 메모리의 낭비가 적다.
• 인접행렬은 정점간의 인접여부를 빠르게 알 수 있지만(O(1)), 희소그래프에서는 메모리의 낭비가 심해질 수 있다.