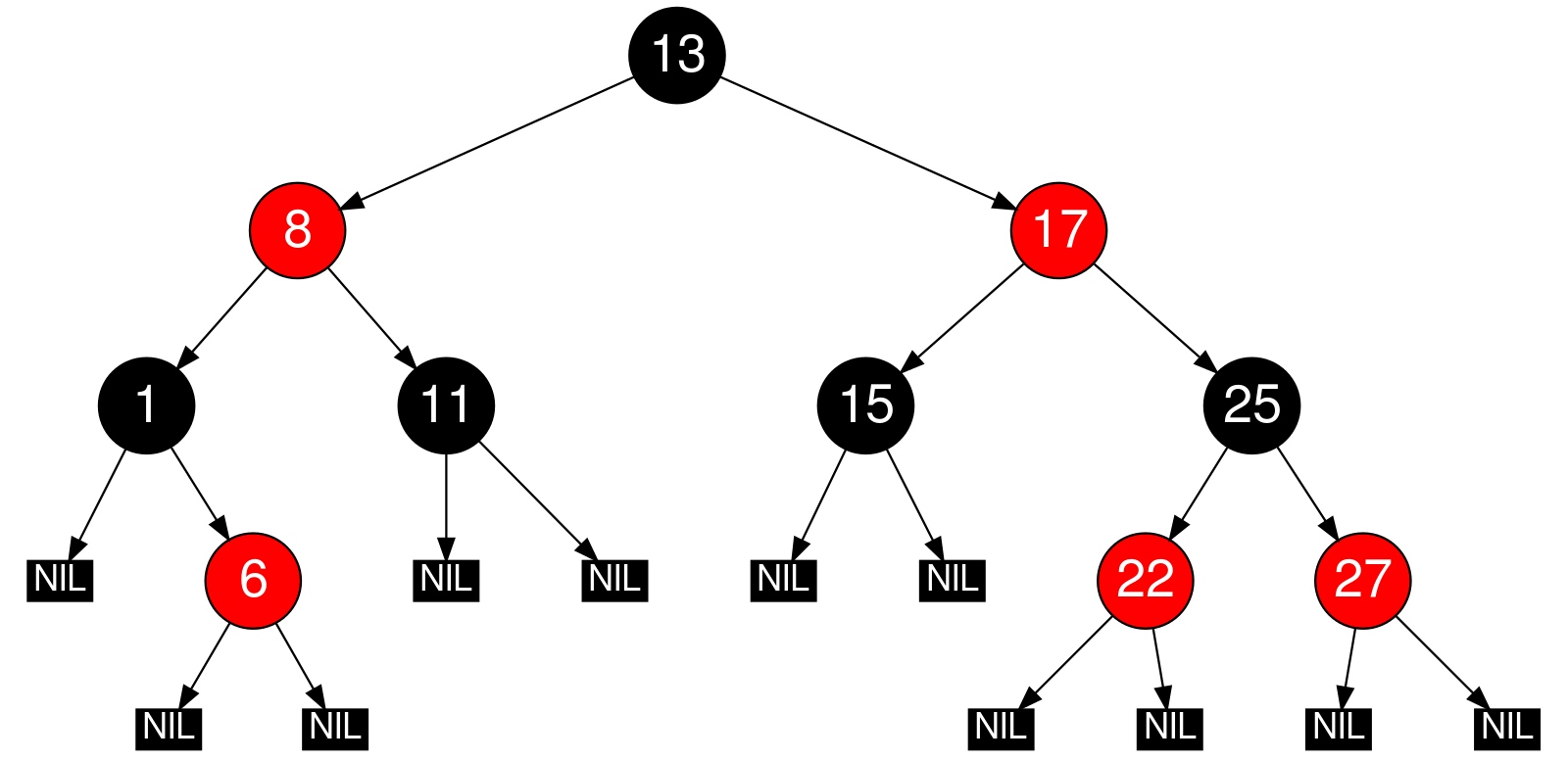
RB 트리란?

레드-블랙 트리(Red-black tree)는 자가 균형 이진 탐색 트리(self-balancing binary search tree)로서, 대표적으로는 연관 배열 등을 구현하는 데 쓰이는 자료구조다. 레드-블랙 트리는 이진 트리의 특수한 형태로서, 컴퓨터 공학 분야에서 숫자 등의 비교 가능한 자료를 정리하는 데 쓰이는 자료구조이다.
레드블랙 트리의 특성
- 모든 노드는 빨간색 혹은 검은색이다.
- 루트 노드는 검은색이다.
- 모든 리프 노드(NIL)들은 검은색이다. (NIL : null leaf, 자료를 갖지 않고 트리의 끝을 나타내는 노드)
- 빨간색 노드의 자식은 검은색이다.
== No Double Red(빨간색 노드가 연속으로 나올 수 없다) - 모든 리프 노드에서 Black Height는 같다.
== 리프노드에서 루트 노드까지 가는 경로에서 만나는 검은색 노드의 개수가 같다.
4번 속성과 5번 속성이 회전과 색변환을 통해 노드를 재배치하게 만드는 이유이다.
레드블랙 트리를 사용하는 이유
이진 탐색 트리의 단점을 보완하기 위해서 쓰는 자료구조.
정렬된 데이터를 이진 탐색 트리로 구현한다면 아래와 같은 모습일 것이다.
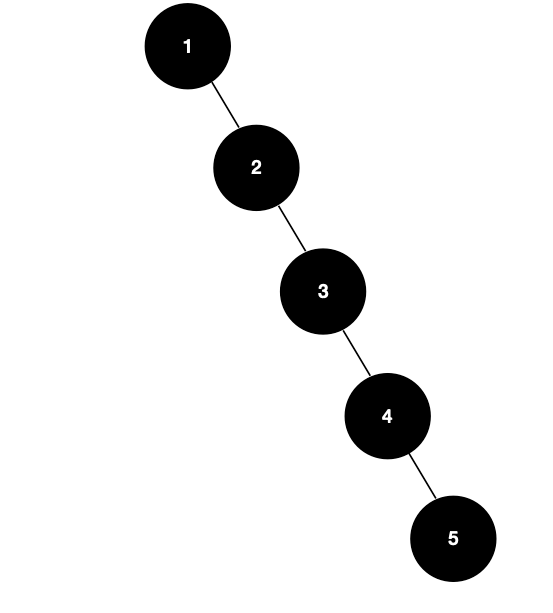
시간복잡도를 따진다면 O(n)이 나와, 이미 정렬된 데이터에 대해서는 비효율적인 자료구조이다.
그러나 레드 블랙 트리의 경우, 최악의 경우에도 O(log n)의 시간복잡도로 삽입, 삭제, 검색을 할 수 있다.
이는 루트 노드부터 가장 먼 리프 노드까지의 거리가, 가장 가까운 노드 경로까지의 거리의 두 배 보다 항상 작다는 특성 때문에 성립한다.
sentinel node
레드블랙트리 코드에서 한계 조건을 다루기 편리하도록 NIL을 표현하기 위해 사용하는 경계 노드이다. 레드블랙 트리에서 경계노드 T.nil은 트리의 다른 보통의 노드와 마찬가지로 동일한 필드를 가진다. 이 노드의 color는 black이지만, 다른 필드 값은 의미를 갖지 않는다.
경계노드를 이용함으로써 노드 x의 NIL자식을 x의 정상적인 자식 노드와 동일하게 다룰 수 있게 된다.
실제 구현할 때는 트리 내 각각의 NIL을 위해 개별적인 경계노드를 사용하는 것보단 저장 공간을 아끼기 위해 하나의 경계 노드 T.nil을 두어서 모든 NIL, 즉, 모든 리프와 루트의 부모를 표현하게 된다.
(모든 NULL 리프에 대한 포인터들이 하나의 NULL 값을 가리키게 설계하는 것이 바람직하다)

Sources:
https://code-lab1.tistory.com/62 [코드 연구소]
https://jwdeveloper.tistory.com/280
https://velog.io/@shinhojung814/WEEK-05-C-레드-블랙-트리
https://dad-rock.tistory.com/355
RBTree 설명 유튜브강의:
part 1: https://www.youtube.com/watch?v=2MdsebfJOyM
part 2: https://www.youtube.com/watch?v=6drLl777k-E
구현 코드)
#include "rbtree.h"
#include <stdlib.h>
void traverse_delete(rbtree *t, node_t *node);
void rbtree_insert_fixup(rbtree *t, node_t *z);
void rbtree_left_rotate(rbtree *t, node_t *x);
void rbtree_right_rotate(rbtree *t, node_t *y);
void rb_transplant(rbtree *t, node_t *u, node_t *v);
node_t *successor(rbtree *t, node_t *cur);
int inorder(node_t *cur, key_t *arr, const rbtree *t, int i, size_t n);
rbtree *new_rbtree(void) {
rbtree *p = (rbtree *)calloc(1, sizeof(rbtree));
// TODO: initialize struct if needed
node_t *nil = (node_t *)calloc(1, sizeof(node_t));
nil->color = RBTREE_BLACK;
p->root = nil;
p->nil = nil;
return p;
}
void delete_rbtree(rbtree *t) {
// TODO: reclaim the tree nodes's memory
node_t *node = t->root;
if (node != t->nil)
traverse_delete(t, node);
// memory of nil node and rbtree struct return
free(t->nil);
free(t);
}
void traverse_delete(rbtree *t, node_t *node) {
if (node->left != t->nil)
traverse_delete(t, node->left);
if (node->right != t->nil)
traverse_delete(t, node->right);
free(node);
}
node_t *rbtree_insert(rbtree *t, const key_t key) {
// TODO: implement insert
node_t *z = (node_t *)malloc(sizeof(node_t));
// new node z initialize
z->key = key;
z->parent = NULL;
z->left = t->nil;
z->right = t->nil;
z->color = RBTREE_RED;
// find location to insert
node_t *y = t->nil;
node_t *x = t->root;
while (x != t->nil) {
y = x;
if (key < x->key) {
x = x->left;
} else {
x = x->right;
}
}
// insert z
z->parent = y;
if (y == t->nil) {
t->root = z;
} else if (key < y->key) {
y->left = z;
} else {
y->right = z;
}
// perform rotation and color change after insertion in order to maintain the properties of rb tree
rbtree_insert_fixup(t, z);
return t->root;
}
void rbtree_insert_fixup(rbtree *t, node_t *z) {
while (z->parent && z->parent->color == RBTREE_RED) {
if (z->parent == z->parent->parent->left) { // case 1: parent is left child of grandparent
node_t *y = z->parent->parent->right;
if (y && y->color == RBTREE_RED) { // case 1.1: uncle is red
z->parent->color = RBTREE_BLACK;
y->color = RBTREE_BLACK;
z->parent->parent->color = RBTREE_RED;
z = z->parent->parent;
} else { // case 1.2: uncle is black
if (z == z->parent->right) { // case 1.2.1: z is a right child
z = z->parent;
rbtree_left_rotate(t, z);
}
// case 1.2.2: z is a left child
z->parent->color = RBTREE_BLACK;
z->parent->parent->color = RBTREE_RED;
rbtree_right_rotate(t, z->parent->parent);
}
} else { // case 2: parent is right child of grandparent
node_t *y = z->parent->parent->left;
if (y && y->color == RBTREE_RED) { // case 2.1: uncle is red
z->parent->color = RBTREE_BLACK;
y->color = RBTREE_BLACK;
z->parent->parent->color = RBTREE_RED;
z = z->parent->parent;
} else { // case 2.2: uncle is black
if (z == z->parent->left) { // case 2.2.1: z is a left child
z = z->parent;
rbtree_right_rotate(t, z);
}
// case 2.2.
z->parent->color = RBTREE_BLACK;
z->parent->parent->color = RBTREE_RED;
rbtree_left_rotate(t, z->parent->parent);
}
}
}
t->root->color = RBTREE_BLACK;
}
void rbtree_left_rotate(rbtree *t, node_t *tmp) {
node_t *x = tmp->right;
tmp->right = x->left;
if (x->left != t->nil) {
x->left->parent = tmp;
}
x->parent = tmp->parent;
if (tmp->parent == t->nil) {
t->root = x;
} else if (tmp == tmp->parent->left) {
tmp->parent->left = x;
} else {
tmp->parent->right = x;
}
x->left = tmp;
tmp->parent = x;
}
void rbtree_right_rotate(rbtree *t, node_t *tmp) {
node_t *x = tmp->left;
tmp->left = x->right;
if (x->right != t->nil) {
x->right->parent = tmp;
}
x->parent = tmp->parent;
if (tmp->parent == t->nil) {
t->root = x;
} else if (tmp == tmp->parent->right) {
tmp->parent->right = x;
} else {
tmp->parent->left = x;
}
x->right = tmp;
tmp->parent = x;
}
node_t *rbtree_find(const rbtree *t, const key_t key) {
// TODO: implement find
node_t *tmp = t->root;
while (tmp != t->nil) {
if (tmp->key == key) {
return tmp;
} else if (tmp->key > key) {
tmp = tmp->left;
} else {
tmp = tmp->right;
}
}
if (tmp == t->nil) {
return NULL;
}
return t->root;
}
node_t *rbtree_min(const rbtree *t) {
// TODO: implement find
node_t *current = t->root;
while (current->left != t->nil)
current = current->left;
return current;
}
node_t *rbtree_max(const rbtree *t) {
// TODO: implement find
node_t *current = t->root;
while (current->right != t->nil)
current = current->right;
return current;
}
//RB Tree에서 지정된 노드p를 제거
int rbtree_erase(rbtree *t, node_t *p) {
//p가 없는 노드이면 삭제 작업 안함
if (p == NULL) {
return 0;
}
// y : 삭제할 노드, x : y의 원래의 위치로 이동할 노드
node_t *y = p;
color_t y_original_color = y->color;
node_t *x;
//p가 오른쪽 자식만 가질 경우
if (p->left == t->nil) {
x = p->right;
rb_transplant(t, p, p->right);
} //p가 왼쪽 자식만 가질 경우
else if (p->right == t->nil) {
x = p->left;
rb_transplant(t, p, p->left);
} //양쪽 자식 모두 가질 경우
else {
//오른쪽 서브트리에서 가장 작은 수 반환
//successor 를 찾는다.
y = successor(t,p->right);
y_original_color = y->color;
x = y->right;
if (y->parent == p) {
x->parent = y;
}
else {
rb_transplant(t, y, y->right);
y->right = p->right;
y->right->parent = y;
}
rb_transplant(t, p, y);
y->left = p->left;
y->left->parent = y;
y->color = p->color;
}
//RB-erase-Fixup------------------------------
if (y_original_color == RBTREE_BLACK) {
while (x != t->root && x->color == RBTREE_BLACK){
if(x == x->parent->left) {
node_t *w = x->parent->right;
if(w->color == RBTREE_RED) {
w->color = RBTREE_BLACK;
x->parent->color = RBTREE_RED;
rbtree_left_rotate(t, x->parent);
w = x->parent->right;
}
if(w->left->color == RBTREE_BLACK && w->right->color == RBTREE_BLACK) {
w->color = RBTREE_RED;
x = x->parent;
}
else {
if (w->right->color == RBTREE_BLACK) {
w->left->color = RBTREE_BLACK;
w->color = RBTREE_RED;
rbtree_right_rotate(t, w);
w = x->parent->right;
}
w->color = x->parent->color;
x->parent->color = RBTREE_BLACK;
w->right->color = RBTREE_BLACK;
rbtree_left_rotate(t, x->parent);
x = t->root;
}
}
else {
node_t *w = x->parent->left;
if(w->color == RBTREE_RED) {
w->color = RBTREE_BLACK;
x->parent->color = RBTREE_RED;
rbtree_right_rotate(t, x->parent);
w = x->parent->left;
}
if(w->right->color == RBTREE_BLACK && w->left->color == RBTREE_BLACK) {
w->color = RBTREE_RED;
x = x->parent;
}
else {
if (w->left->color == RBTREE_BLACK) {
w->right->color = RBTREE_BLACK;
w->color = RBTREE_RED;
rbtree_left_rotate(t, w);
w = x->parent->left;
}
w->color = x->parent->color;
x->parent->color = RBTREE_BLACK;
w->left->color = RBTREE_BLACK;
rbtree_right_rotate(t, x->parent);
x = t->root;
}
}
}
x->color = RBTREE_BLACK;
}
free(p);
return 0;
}
//u : 삭제할 노드, v : u의 자식 노드 - u의 부모 노드와 연결되어야 한다.
void rb_transplant(rbtree *t, node_t *u, node_t *v) {
if (u->parent == t->nil) {
t->root = v;
}
else if (u == u->parent->left) {
u->parent->left = v;
}
else {
u->parent->right = v;
}
v->parent = u->parent;
}
node_t *successor(rbtree *t, node_t *cur) {
node_t *n = cur;
while(n->left != t->nil) {
n = n->left;
}
return n;
}
int inorder(node_t *cur, key_t *arr, const rbtree *t, int i, size_t n) {
if (i < n) {
if (cur->left != t->nil) {
i = inorder(cur->left, arr, t, i, n);
}
arr[i++] = cur->key;
if (cur->right != t->nil) {
i = inorder(cur->right, arr, t, i, n);
}
}
return i;
}
int rbtree_to_array(const rbtree *t, key_t *arr, const size_t n) {
// TODO: implement to_array
if (!inorder(t->root, arr, t, 0, n)) {
return 1;
}
return 0;
}