탐욕 알고리즘 (Greedy Algorithm)
- 현재 상황에서 당장 가장 좋아 보이는 상황만을 선택하는 알고리즘
- 주로 최적의 해를 구하기 위한 근사적인 방법으로 사용한다.
주로 코딩 테스트에서 앞 부분 쉬운 문제로 출제된다고 한다.
예시
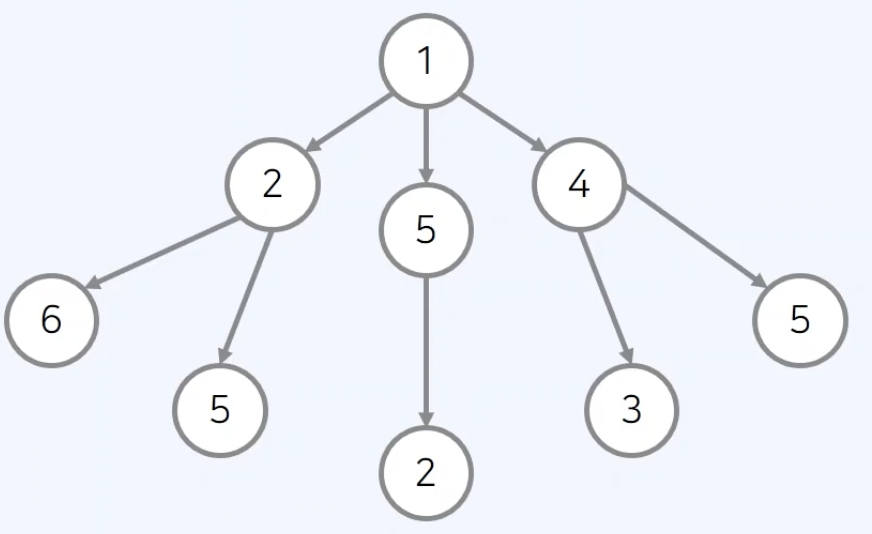
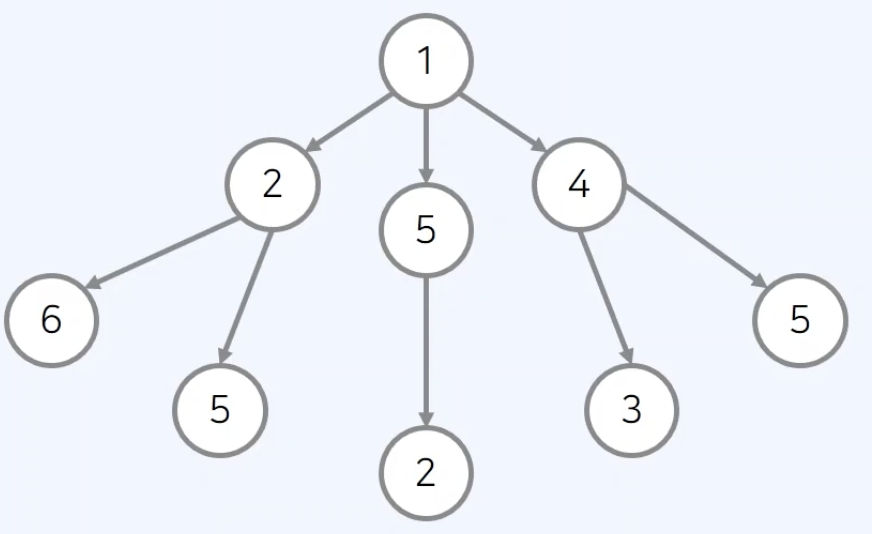
- 해당 그래프에서 루트에서 단말 노드까지 거쳐가는 노드의 가장 큰 합을 고를 때 최적의 해는 1->4->5 합 10이다.
- 하지만
greedy하게 풀 경우
root(1) -> 선택지 (2, 5, 4) -> greedy(5) -> greedy (2) 합 8이다.
즉, 항상 최적의 해를 보장해주는 알고리즘이 아니다. (탐색의 범위를 줄여주기 때문에 시간 복잡도가 상대적으로 낮다.)
탐욕 알고리즘과 근사 해
- 단순한 탐욕 알고리즘으로는 최적의 해를 놓칠 수 있다.
- 하지만, 최적의 해에 가까운 값을 찾고,
근사 해를 찾을 때 시간 복잡도가 낮아 자주 채택된다. - 하지만 일반적으로
문제에선 탐욕 방법으로 최적의 해가 보장되는 문제가 많다.
최적의 해 === 탐욕 방법 결과 해
탐욕 알고리즘의 접근 방법
- 방법 고안 : 현재 상황에서 어떤 알고리즘을 사용할지 고안
- 정당성 확인 : 고안한 알고리즘이 항상 최적의 해를 보장하는지 확인한다.
알고리즘 맛보기
- 거스름 돈 문제
- 동전을 이용해 거슬러 주어야 할 때, 동전 개수의 최소 값을 구하는 문제
해결 방법
- 가장 큰 화폐 단위부터 거슬러 주는 것이다.
500 -> 100 -> 50 -> 10 원 순으로 거슬러 줄 수 있을 만큼 거슬러 주면 최소 개수를 찾을 수 있다.
정당성 분석
- 단순히 큰 화폐 단위부터 선택하여 최적의 해를 찾을 수 있는 이유는 화폐 단위가 배수 관계에 속하기 때문이다.
- ex) 120원을 거슬러 줄 때 80, 60, 10원 동전이 있다면 최적의 해는 60원 동전 2개이다.
탐욕적으로 80원을 선택하면 5개의 동전이 필요하게 된다. - 이 처럼 모든 상황에서 최적의 해를 찾는 방법은 아니지만, 정당성 분석이 잘 되었다면 좋은 시간 복잡도로 최적의 해를 찾을 수 있는 방법이다.
