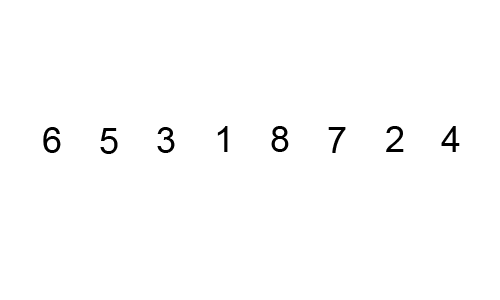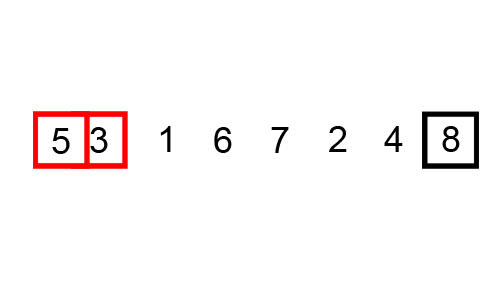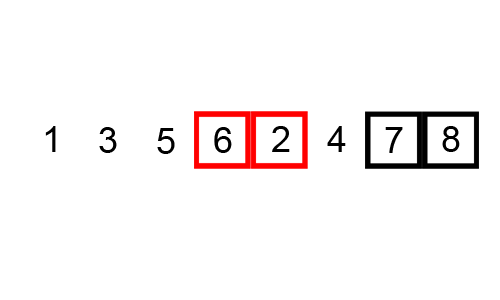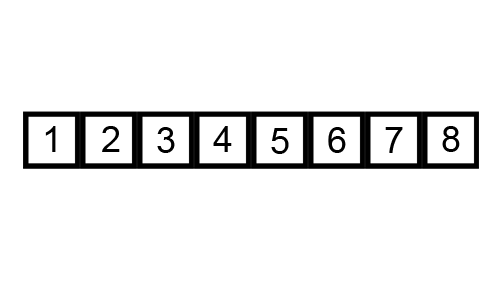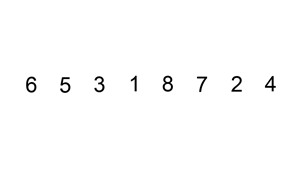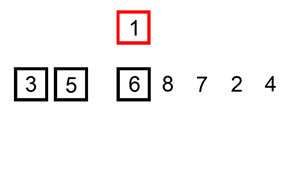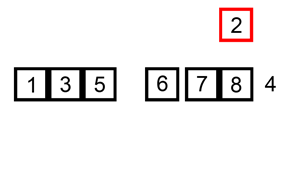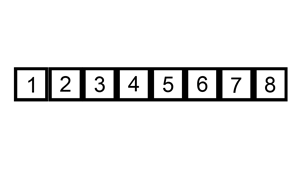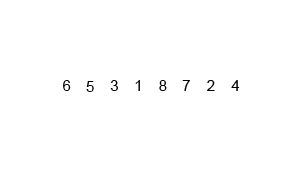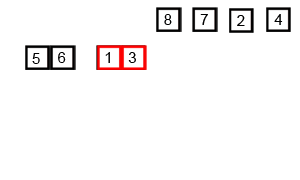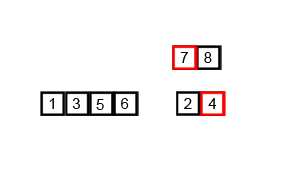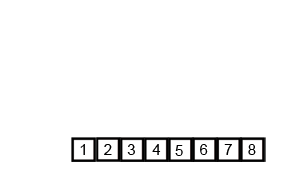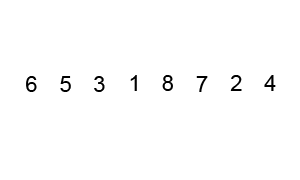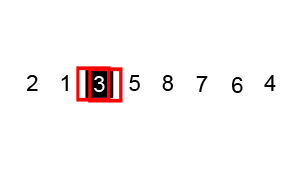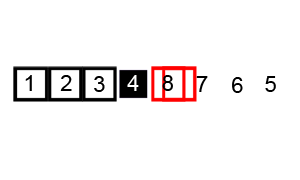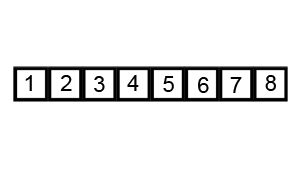1. 선택정렬 (Selection Sort)
앞에서부터 차례대로 정렬하는 방법이다. 먼저 주어진 리스트 중에 최소값을 찾고 그 값을 맨 앞에 위치한 값과 교체하는 방식으로 진행하는 정렬방법이다.
최적 효율은 내림차순으로 정렬되어 있는 자료를 오름차순으로 정렬할 때이며, 반대로 이미 정렬된 상태에서 소수 자료가 추가됨으로 재정렬하게 될 때에는 최악의 처리 속도를 보여준다.
Java 구현
2. 버블정렬 (Bubble Sort)
첫 번째 원소부터 인접한 원소끼리 계속 자리를 교환하면서 맨 끝부터 정렬하는 방식을 말한다.
데이터를 하나씩 비교할 수 있어 정밀하게 비교 가능하나 비교횟수가 많아지므로 성능면에서 좋은 방법이 아니다.
Java 구현
3. 삽입정렬 (Insertion Sort)
자료 배열의 모든 요소를 앞에서부터 차례대로 이미 정렬된 배열 부분과 비교하여 자신의 위치를 찾아 삽입함으로써 정렬을 완성하는 정렬 방법이다.
버블정렬의 비교횟수를 줄이고 보다 좋은 성능 효율을 보여준다.
Java 구현
4. 합병정렬 (Merge Sort)
작은 단위로 잘게 쪼개어 작은 단위부터 정렬해서 정렬된 단위들을 계속 병합해가는 정렬 방식이다.
간단하고 쉽고 안정성이 있어 좋은 성능을 보여준다. 공간이 많이 필요하다는 단점이 있다.
5. 퀵 정렬 (Quick Sort)
연속적인 분할에 의한 정렬 방식이다. 처음 하나의 축(Pivot)을 정하여 이 축의 값보다 작은 값은 왼쪽에 큰 값은 오른쪽으로 위치시킨뒤 왼쪽과 오른쪽의 수 들은 다시 각각의 축으로 나누어져 축값이 1이 될 때까지 정렬한다.
가장 많이 사용되나 안정성이 떨어진다는 단점이 있다.
Java 구현
6. 힙 정렬 (Heap Sort)
최대 힙 트리나 최소 힙 트리를 구성해 정렬하는 방법이다. 모든 노드가 힙 속성(각 노드의 값이 자신의 자식노드 값보다 큰 이진트리)을 만족하도록 재귀적으로 트리 구조를 만들어 정렬을 완성한다.
부가적인 메모리가 전혀 필요없다는 게 큰 장점이다.
참고) https://coding-factory.tistory.com/615, https://d2.naver.com/helloworld/0315536그 외 쉘 정렬(Shell Sort), 기수 정렬(Radix Sort) 등이 있다.
✔︎ 정렬 알고리즘 예상질문
Quick sort가 항상 빠르고 좋은가?
정렬하고자 하는 데이터의 크기 n이 작을때를 가정해보자. 계속해서 재귀적으로 partition 함수를 호출하는 quick sort로만 정렬한다면 n이 작을 때 function call 하는 비용이 더 많이 들것이다. 즉, n이 작아진 경우에는 다른 sorting algorithm을 통해 정렬하는 것이 더 효율적일 수 있다. n 값이 작을 때, nlongn 과 n^2 차이는 미미하므로 Insertion sort로 구현하는 것이 더 효율적일 수 있다. 실제로 Java에서 quick sort의 구현이 이렇게 되어있다. n값이 작을 때는 Insertion sort로 정렬한다.
Merge sort는 언제 쓰일까?
한정된 메모리 상황에서 ‘빅 데이터'를 정렬해야 하는 경우를 가정하자. 기존의 정렬 알고리즘으로 한번에 정렬 할 수 없는.. 디스크에서 읽어오는데 데이터 전부를 메모리에 올리지 못하는 경우 말이다. 그래서 이 큰 문제를 작은 문제로 나누어(Divide) 정렬한다. 작은 문제로 나누어진 데이터를 quick sort로 정렬한 뒤(Conquer) 각각 정렬된 데이터들을 다시 합쳐야한다(Combine). 하지만 그냥 combine 한다면 작은 문제로 정렬한 의미가 없어지므로 이 경우에 merge sort 를 사용하여 combine 하는 것이다. 즉, Merge sort는 DB에 많이 쓰인다.
참고
이미지 출처 - 위키 백과