BOJ 2263 트리의 순회

트리의 순회 방법의 특징들을 알면 풀 수 있는 문제. 특히 순회 별 트리의 root를 찾는 방법이 중요하다.

• 중위순회 Inorder Traversal: left - root - right 순서로 순회. root를 중간에 순회한다.
• 전위순회 Preorder Traversal: root - left - right 순서로 순회. root를 가장 처음에 순회한다.
• 후위순회 Postorder Traversal: left - right - root 순서로 순회. root를 가장 마지막에 순회한다.

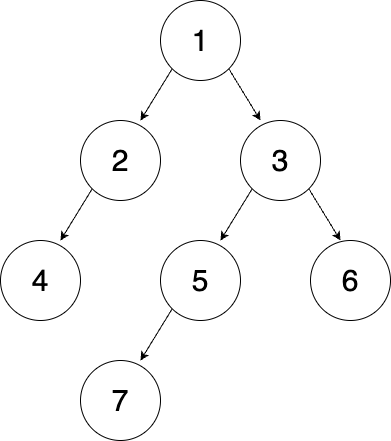
위와 같은 트리를 중위순회하는 경우와 후위순회하는 경우의 결과는 다음과 같다.

• 중위순회: 4 2 1 7 5 3 6
• 후위순회: 4 2 7 5 6 3 1

1단계: root 찾기

이때 root를 찾는 가장 간단한 방법은 후위순회의 마지막 숫자가 root라는 점을 이용하는 것이다. 따라서 위 경우의 root가 1이라는 것을 알 수 있다. 이 값을 결과를 저장할 배열에 append한다.

2단계: left, right 찾기

다음으로는 중위순회에서 root의 위치를 찾는다. 그 점을 기준으로 이전 값들이 left, 이후 값들이 right이다. 4 2 1 7 5 3 6에서 1의 이전값인 4 2가 left고 7 5 3 6이 right이다.

3단계: 후위순회 결과 나누기

4 2가 left고 7 5 3 6이 right인 점을 이용해 후위순회 결과를 둘로 나눈다. left의 원소가 2개이고 right의 원소가 4개이므로 후위순회의 결과를 앞 2개, 뒤 4개로 나눈다.

4단계: 나뉜 결과로 재귀(분할정복)

left로 1단계부터 다시, right로 1단계부터 다시한다. 트리의 left, right 역시 트리이므로, 큰 문제가 작은 두 문제로 나뉘는 분할정복의 형태임을 알 수 있다.

코드 전체

import sys

input = sys.stdin.readline
sys.setrecursionlimit(100005)

n = int(input())
inorder_arr = list(map(int, input().split()))
inorder_idx = {inorder_arr[i]: i for i in range(n)}
postorder_arr = list(map(int, input().split()))

answer = []


def preorder(in_start: int = 0, in_end: int = n - 1, post_start: int = 0, post_end: int = n - 1):
    if in_start > in_end:
        return
    root = postorder_arr[post_end]
    answer.append(root)
    if in_start == in_end:
        return
    in_root_idx: int = inorder_idx[root]
    left_len = in_root_idx - in_start

    preorder(in_start, in_root_idx - 1, post_start, post_start + left_len - 1)
    preorder(in_root_idx + 1, in_end, post_start + left_len, post_end - 1)


def main():
    preorder()
    print(*answer)


if __name__ == '__main__':
    main()