BOJ 9251 LCS

이 문제는 점화식을 아예 외워두는 것이 의미가 있을 것 같아서 기록해둔다.

LCS는 Longest Common Subsequence의 줄임말로, 두 수열(문자열)의 부분 수열 중 일치하는 최장의 수열을 의미한다. 문제에서 준 예시를 보면, ACAYKP와 CAPCAK LCS는 ACAK가 된다.

이 문제의 점화식은 두 문자열을 반복문으로 비교하면서 같은 문자를 찾은 경우와 아닌 경우가 나누어 생각한다.

• 같은 문자인 경우 해당 문자를 보기 전까지 두 문자열의 LCS에 그 문자를 더하면 된다.
• 다른 문자인 경우 그 문자를 첫 문자열에서 뺀 경우와의 LCS와 두번째 문자열에서 뺀 경우와의 LCS 중 더 긴 것을 선택한다.

말로 쓰면 좀 어려운데, 점화식으로 표현하면 간단하다. 점화식을 만들기 위해 필요한 변수들을 먼저 선언하자.

1. 두 문자열 정의

import sys
first_str = sys.stdin.readline().rstrip()
second_str = sys.stdin.readline().rstrip()

2. DP를 위해 메모이제이션을 할 배열 생성

dp = [[0] * (len(second_str) + 1) for _ in range(len(first_str) + 1)]

3. 두 문자열을 반복문으로 돌면서, 같은 문자인지 확인

for i in range(len(first_str)):
    a = first_str[i]
    for j in range(len(second_str)):
        b = second_str[j]
        if a == b:
            dp[i + 1][j + 1] = dp[i][j] + 1
        else:
            dp[i + 1][j + 1] = max(dp[i + 1][j], dp[i][j + 1])

3번 과정을 그림으로 표현하면 아래와 같다.

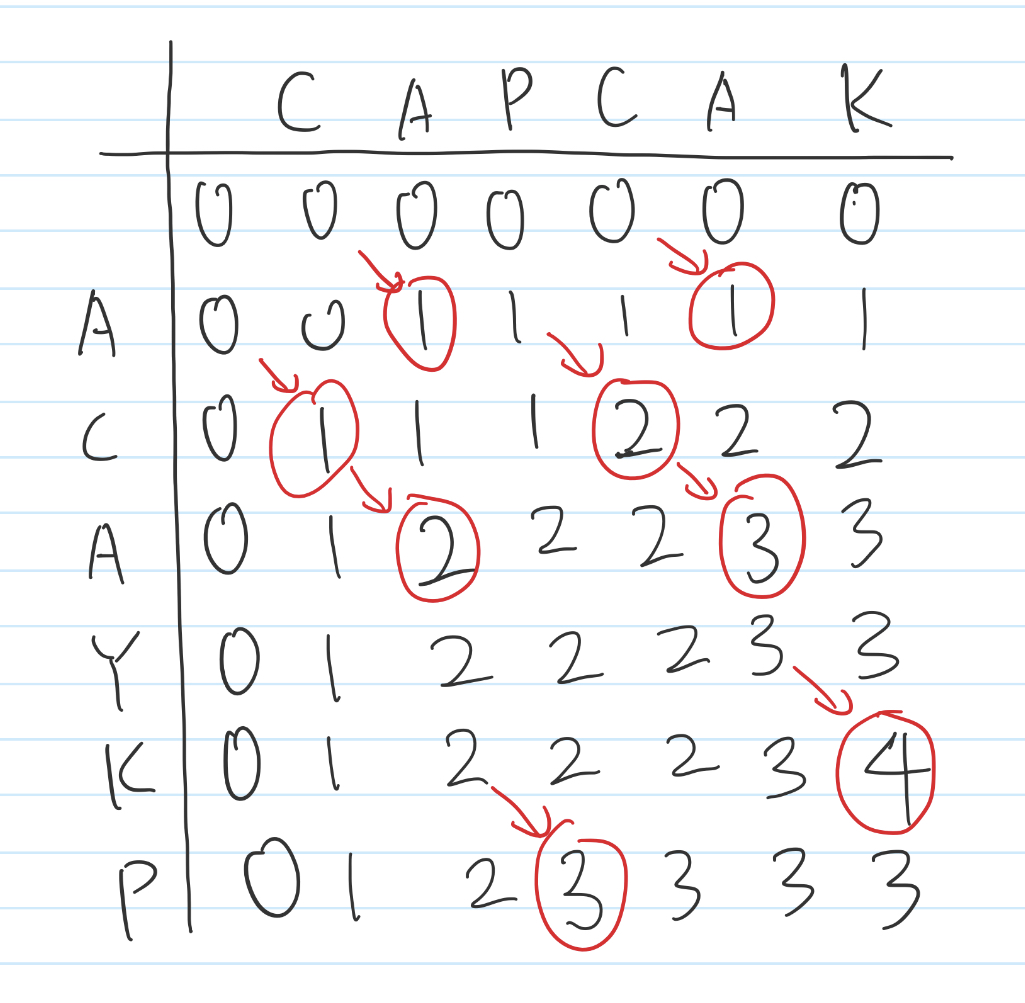
점화식 부분만 보면

if first_str[i] == second_str[j]:
	dp[i+1][j+1] = dp[i][j] + 1
else:
	dp[i+1][j+1] = max(dp[i+1][j], dp[i][j+1])

직관적으로 생각하면 같은 문자를 발견했을 때 이전의 LCS보다 1 길어져야 하고, 아닌 경우엔 이전의 LCS를 사용하는 것이다.

이리저리 다른 문제로 활용이 많이 될 수 있을 것 같은 알고리즘이니 잘 알아두자.