Programmers 행렬과 연산 [2022 KAKAO TECH INTERNSHIP]

문제링크

카카오의 해설을 참고했습니다.

Intro

오랜만에 쓰는 글...자주 좀 써 봅시다.

ShiftRow

ShiftRow 연산은 마지막 행을 첫 행으로 바꾸는 것이므로 파이썬의 list를 통해 간단히 연산 가능하지만, 스택과 큐의 연산에 초점을 맞춰 구현된 deque를 쓰도록 하자.

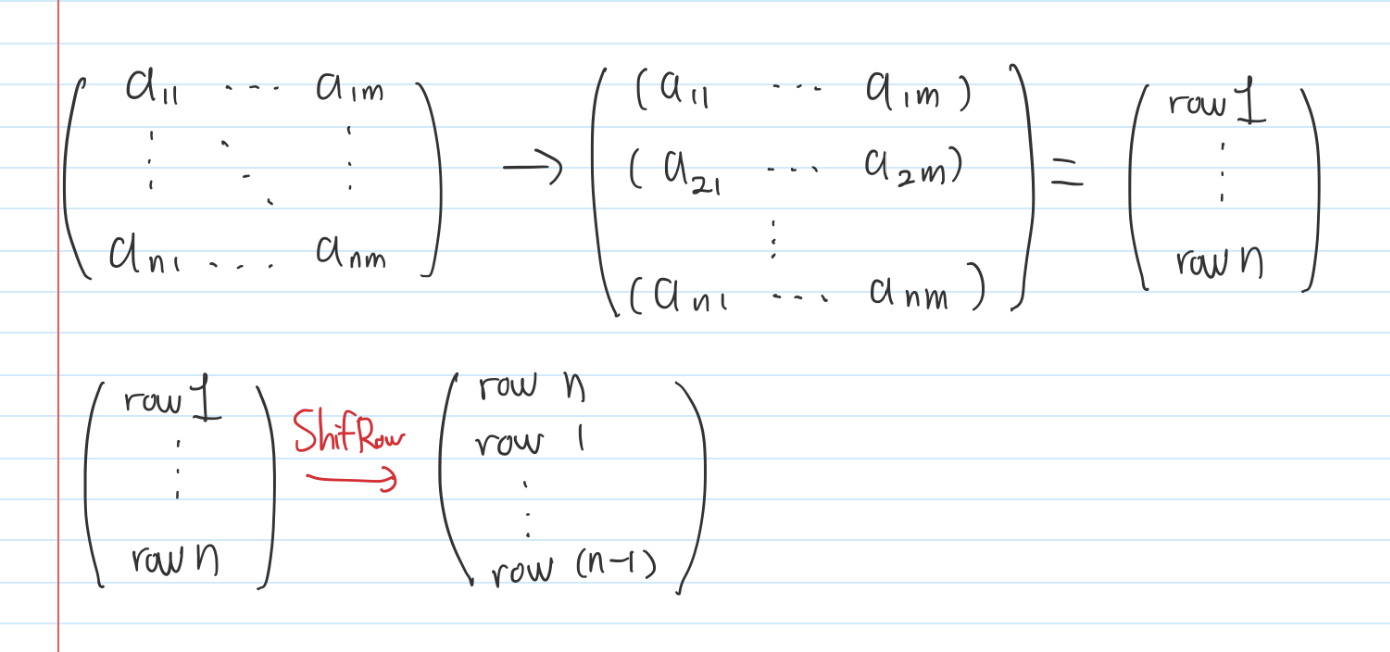
rows = deque(row for row in rc)
# ShiftRow
rows.appendleft(rows.pop()). 

Rotate

이 문제의 핵심은 Rotate 연산이다. 하나의 행렬로 전체를 다룰 경우 이 연산 때문에 시간 에러가 난다. 한 번의 연산에서 행의 수 * 2 + 열의 수 * 2만큼 연산을 수행하는데 이를 operations의 길이만큼 수행할 수 있으므로, 최대로 5만 * 5만 * 10만의 연산이 수행된다.

따라서 행렬을 분해해서 본다면 문제는 쉬워진다. 연산은 첫 행, 마지막 행, 첫 열, 마지막 열 이렇게 4 경우만 생각하면 되므로 해당 행과 열들만 신경 쓰면 되는 모습으로 분해해주자.
첫 행, 마지막 행은 ShiftRow를 부분과 같이 전체 행렬을 행으로 나눠 생각하는 방식이 이미 고려하고 있다. 따라서 첫 열, 마지막 열을 고려하는 구조만 생각하면 된다.
카카오의 정식 해설은 아래와 같은 분해를 추천한다. 아래 그림과 같이 분해할 경우 4개의 deque의 간단한 pop과 append 연산만으로 Rotate 연산을 손쉽게 구현할 수 있다.

N = len(rc)
M = len(rc[0])
left_col = deque([rc[i][0] for i in range(N)])
right_col = deque([rc[i][M-1] for i in range(N)])
rows = deque([deque(rc[i][1:M-1]) for i in range(N)])

# Rotate
rows[0].appendleft(left_col.popleft())
right_col.appendleft(rows[0].pop())
rows[N-1].append(right_col.pop())
left_col.append(rows[N-1].popleft())

Code

from collections import deque


def solution(rc, operations):
    N = len(rc)
    M = len(rc[0])
    left_col = deque([rc[i][0] for i in range(N)])
    right_col = deque([rc[i][M - 1] for i in range(N)])
    rows = deque([deque(rc[i][1:M - 1]) for i in range(N)])

    for op in operations:
        if op == 'ShiftRow':
            left_col.appendleft(left_col.pop())
            rows.appendleft(rows.pop())
            right_col.appendleft(right_col.pop())
        else:  # 'Rotate'
            rows[0].appendleft(left_col.popleft())
            right_col.appendleft(rows[0].pop())
            rows[N - 1].append(right_col.pop())
            left_col.append(rows[N - 1].popleft())
    answer = []
    for i in range(N):
        answer.append([left_col[i]] + list(rows[i]) + [right_col[i]])
    return answer