다음은 DFA와 NFA의 동치성에 대해서 공유하고자 한다.
우선 필기부터 첨부한다.
NFA와 DFA의 동치성에서 중요한 개념은, 어떤 언어(문법)에 대한 NFA가 있으면, 해당 NFA에 대한 DFA도 존재한다는 것이다. (반대도 마찬가지)
DFA는 본질적으로 NFA의 한 제한된 종류이므로, DFA에 의해 인식되는 모든 언어는 어떤 NFA에 의해서도 인식이 가능하다는 것이다.
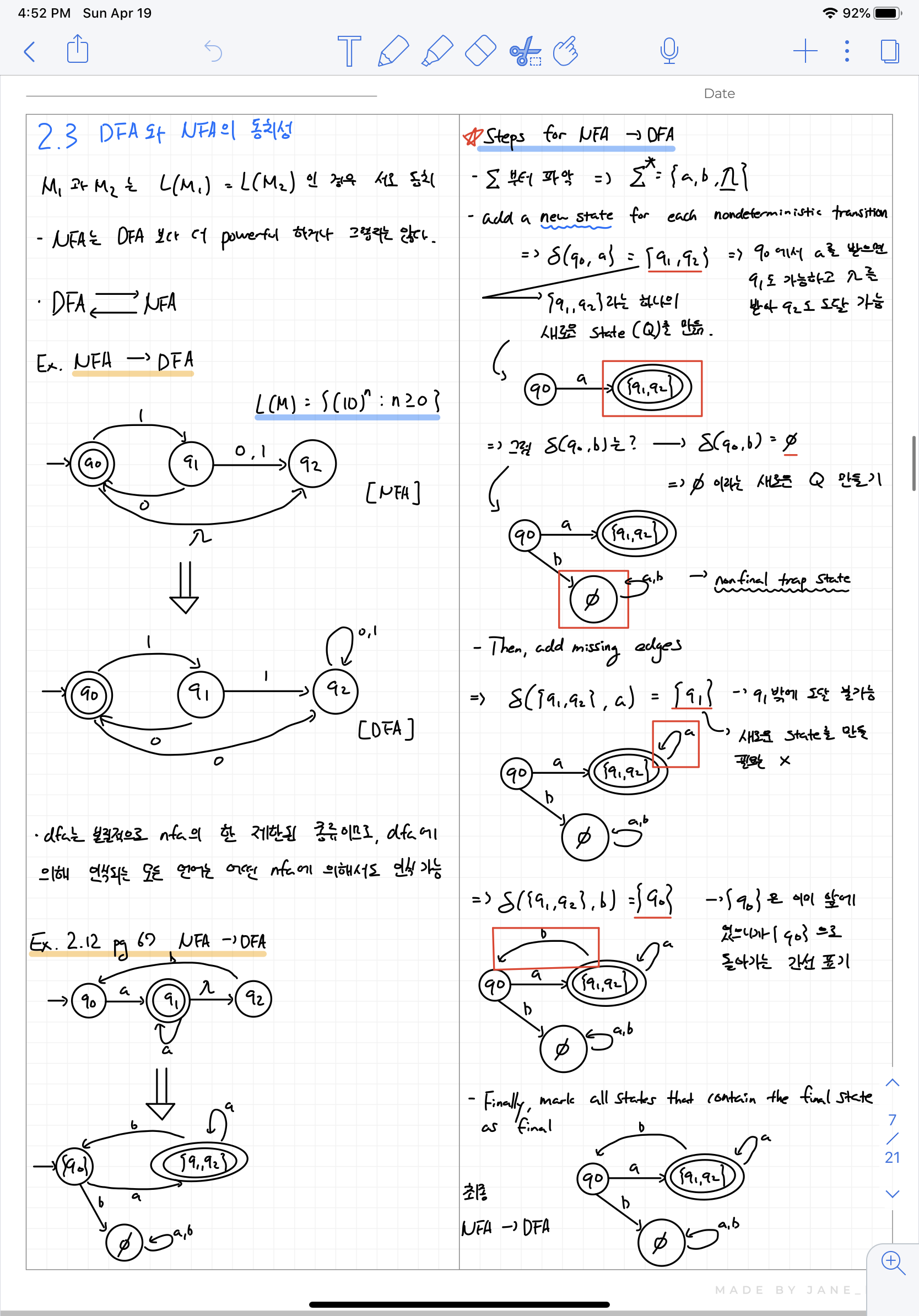
즉, 위와 같은 언어가 있고, 이를 표현한 NFA가 있다고 가정하자. 그럼 이와 같은 문법을 인식하는 DFA도 있다는 뜻이다.
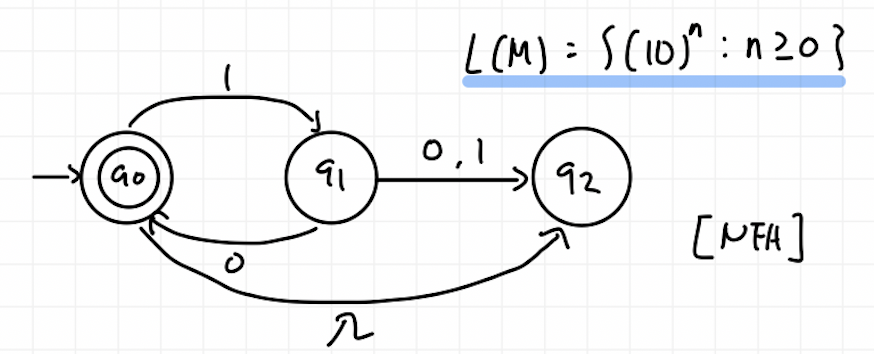
DFA의 핵심은 각 State에 input alphabet 중 하나가 들어왔을 시 나아가는 방향이 정의되어 있어야 한다는 것이다. 즉, NFA에서는 (q0,1)만 정의되어 있어도 문제가 없는데, DFA에서는 (q0,1) 뿐만 아니라 (q0,0)까지도 정의가 되어있어야 한다. 그렇게 해서 표현한 것이 위의 DFA다.
NFA->DFA 변환 과정
NFA에서 DFA로 변환시키려면 몇 가지 과정을 거쳐야 한다. Textbook 에 나온 step 부터 살펴보자.
- Add a new state for each nondeterministic transition
- Then, add missing states
- Finally, mark all states that contain the final state as final (double circle).
예시를 하나 살펴보자:
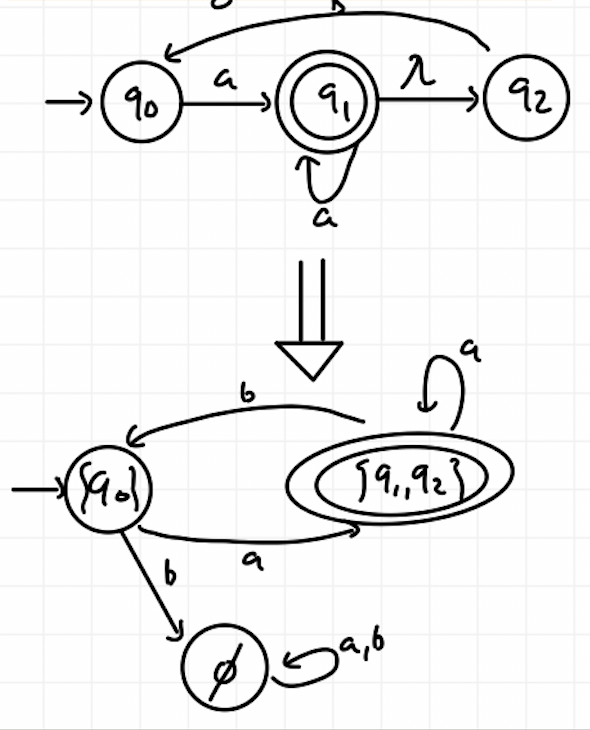
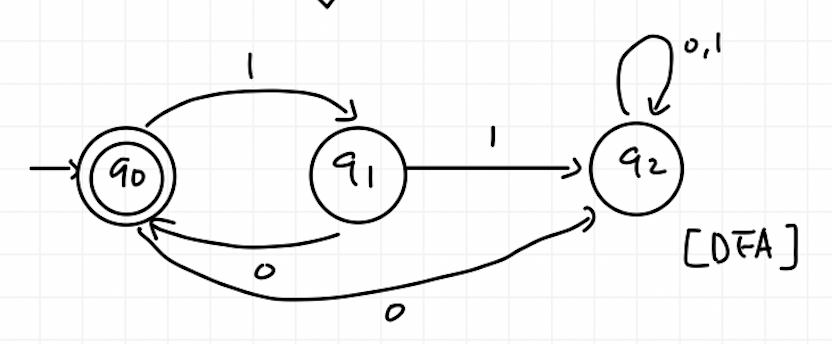
위가 NFA고, 아래가 DFA다.
q0에서 a를 받으면 q1으로 갈 수도 있고, 람다를 추가로 받아 q2로도 갈 수가 있다. 그렇기 때문에 (q0,a)={q1,q2}가 되어 {q1,q2}를 하나의 새로운 state로 지정하게 되었다. {q1,q2}에서 a를 받으면 q1과 q2에게만 갈 수 있게 때문에 다른 state로 지정할 필요 없이 스스로에게 loop을 돌리면 된다.
{q1,q2}에서 b를 받으면 갈 수 있는 곳이 q0 밖에 없어 다시 q0으로 돌아가는 vertex를 그려주면 된다.
마지막으로, NFA에서는 q0에서 b를 받는 walk가 정의되어 있지 않다. NFA에서는 무방하지만, DFA에서는 모든 시그마에 대한 정의가 되어 있어야 하기 때문에 따로 저렇게 공집합으로 빼내어, trap state로 지정해주었다.
이렇게 해서 NFA와 DFA의 동치성에 대해서 간략하게 알아봄과 동시에 NFA에서 DFA 변환 과정도 간단하게 살펴보았다.
