[Leetcode] 221. Maximal Square (C++)

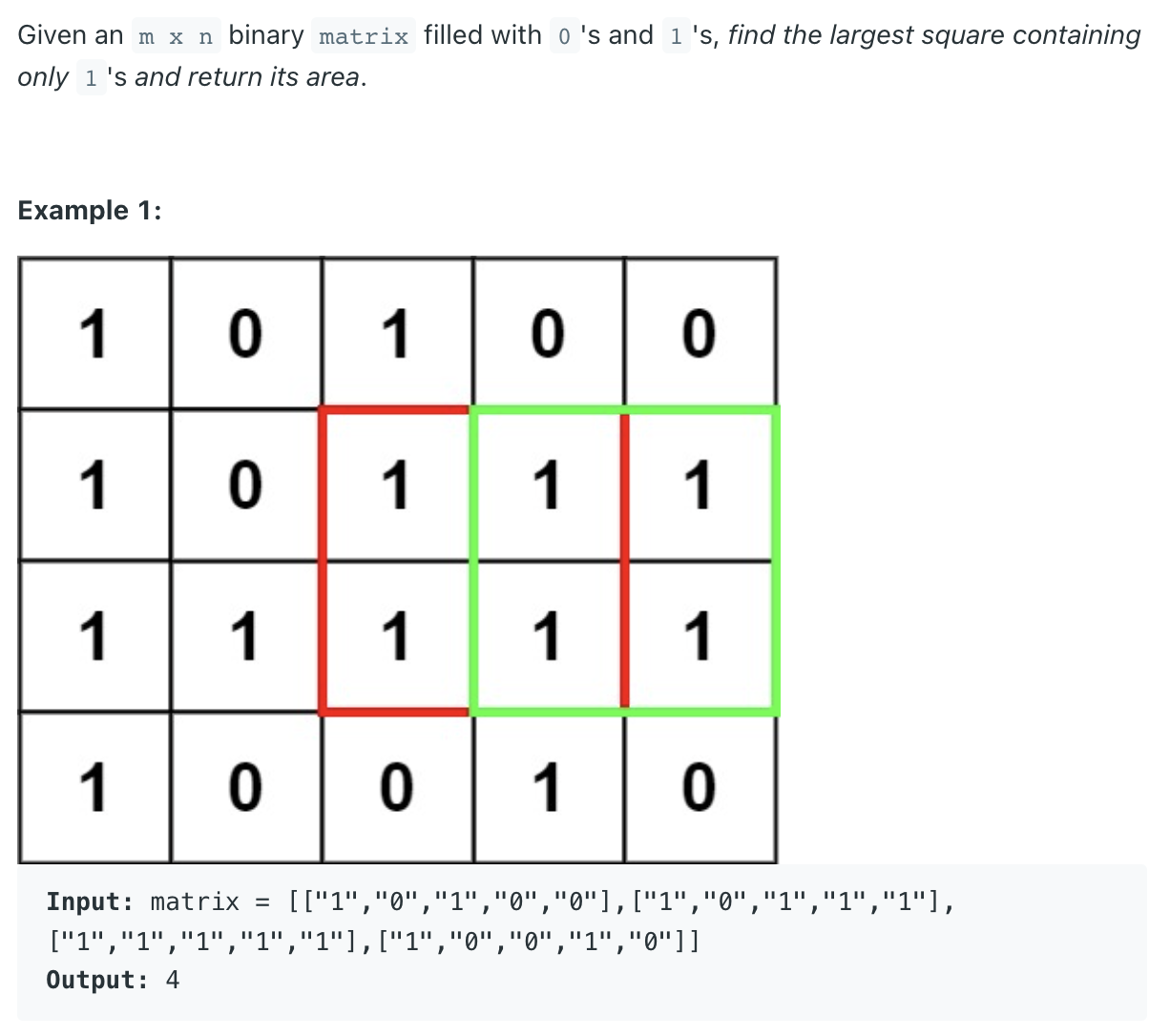
문제

221. Maximal Square

코드

// brute force

class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        int answer = 0;
        for (int i = 0; i < matrix.size(); i++){
            for (int j = 0; j < matrix[0].size(); j++){
                if (matrix[i][j] == '1') 
                    answer = max(answer, check(matrix, i, j));
            }
        }
        return answer;
    }
    
    int check(vector<vector<char>>& matrix, int x, int y){
        int len = 1;
        while(len){
            bool flag = true;
            for (int i = 0; i < len; i++){
                for (int j = 0; j < len; j++){
                    if (!(x+i < matrix.size() and y+j < matrix[0].size()) or matrix[x+i][y+j] == '0') {flag = false; break;}   
                }
                if (!flag) break;
            }
            if (!flag) break;
            len++;
        }
        
        return (len-1)*(len-1);
    }
};

// dynamic programming

class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        int rows = matrix.size(), cols = matrix[0].size(), M = 0;
        vector<vector<int>> dp(rows+1, vector<int>(cols+1, 0));
        
        for (int i = 1; i <= rows; i++){
            for (int j = 1; j <= cols; j++){
                if (matrix[i-1][j-1] == '1'){
                    dp[i][j] = min(min(dp[i][j-1], dp[i-1][j]), dp[i-1][j-1]) + 1;
                    M = max(M, dp[i][j]);
                }
            }
        }
        return M*M;   
    }
};

접근

먼저 단순하게 생각했다. 실제로 matrix를 순회하면서 1인 칸에서 한 변의 길이가 1,2,3 ... 이 될 수 있는지 확인하는 것이다. 금방 알 수 있겠지만 이 방법은 답은 구할 수 있지만 굉장히 시간이 많이 걸리게 된다. 때문에 다른 방법을 고민해보았다.

칸에 해당하는 값이 이 칸을 포함해서 만들 수 있는 정사각형의 최대 변의 길이라고 생각해보자. 그렇다면 이 칸의 값은 윗칸, 왼쪽칸, 왼쪽윗칸의 값에 영향을 받을 것이다. 아직 살펴보지 않은 나머지 칸을 제외하고 이들 중 가장 작은 값을 구하고 이에 1을 더해주면 현재 살펴보는 칸의 값이 된다. 이유는 비교하는 칸들이 모두 1이라면 현재 칸을 포함해서 변의 길이가 2인 정사각형을 이룰 수 있고, 이는 칸들이 각기 다른 값을 가지고 있는 경우에도 현재 칸을 포함해서 정사각형을 이룰 수 있게 되기 때문이다. 따라서 현재 칸의 값을 갱신하고 매번 최대값을 비교하여 유지하였다.