머신러닝 기본 용어

회귀(Regression)와 분류(Classification)

회귀(regression)

• 입력값 : 연속값(실수형), 이산값(범주형) 등 모두 가능
  ex) 연속값 - 1,2,3, / 이산값 - 병에걸렸다, 걸리지않았다.
• 출력값 : 연속값(실수형)
• 모델 형태 : 일반적인 함수 형태
  • y = w1x + w0

분류(classification)

• 입력값 : 연속값(실수형), 이산값(범주형) 등 모두 가능
• 출력값 : 이산값(범주형)
• 모델 형태 : 이진 분류라면 시그모이드(sigmoid) 함수, 다중 분류
  • 이진분류 : 클래스의 개수가 2개인 상황
  • 다중분류 : 클래스의 개수가 여러개인 상황
  • 클래스는 병에 걸린 상황, 병에 걸리지 않은 상황 등 각각의 케이스를 의미한다.

용어

데이터의 구성

• 데이터는 피처(feature)와 라벨(label)로 구성됨
  • 라벨은 맞추고 싶어하는 목표를 의미
• 이는 독립 변수와 종속 변수로도 불림
• 라벨은 y로 표시하며, 라벨의 유무로 지도학습, 비지도학습으로 구분
  • 라벨로 이산값을 줬을 때는 분류 문제, 라벨로 연속값을 줬을 때는 회귀 문제를 푼다고 생각하면 된다.

Feature(=attribute, 피처)

• 데이터 x의 특징, 혹은 항목을 의미
• N : 데이터 샘플 개수, D(P) : 피처의 갯수
  
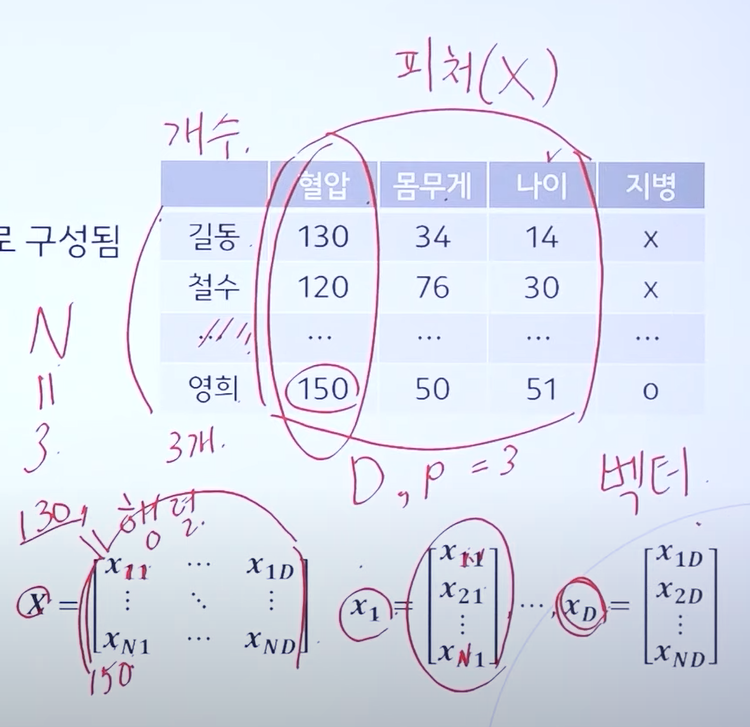
• N과 D의 조합을 행렬(matrix) 형태로 표현
• 피처 단독에 대해서 백터 형태로 표현

Parameter(=weight, 파라미터, 가중치)

• 주어진 데이터(입력값) 말고, 모델(함수)이 가지고 있는 학습 가능한(leanable) 파라미터
• 즉, 가중치
  ex) y = ax + b의 형태에서 y와 x는 데이터이고 a, b는 파라미터로 분류할 수 있다.
• 보통 weight의 w를 따서 w0 ~~~ wD까지 표현한다.

Hyperparameter(하이퍼 파라미터)

• 모델 학습에 있어, 인간이 정해야 하는 변수들
• 학습률, 배치 크기 등등

input(입력값) vs output(출력값)

• input : 인간이 주는 데이터 중 피처 부분만(x로 표기)
• output : 모델로부터 출력되는 예측값(y^로 표기)
• y(라벨과) y^의 차이를 손실값이라고 한다.
  
  

선형 모델 vs 비선형 모델

• Linear regression(선형 회귀)
  • 파라미터를 선형 결합식으로 표현 가능한 모델
  • 선형 결합식이란 가중치와 데이터가 1차식으로 결합된 것
  • 데이터가 x2, x3이든 상관없다, 이를 a, b든 다른 문자로 치환하면 결국 weight와는 1차식으로 결합된다.
    ex) y = w0 + w1x1 + w2x2 + ... + wDxD
    ex) y = w0 + w1x1 + w2x2
• Nonlinear regrestion (비선형 회귀)
  • 선형 결합식으로 표현 불가능한 모델
    ex) log(y) = w0 + w1log(x)>
• 참고로 선형회귀와 비선형 회귀는 데이터의 결합방식을 의미하는 것이고, 결정경계의 선형, 비선형의 경우 데이터를 나누는 경계가 선혀으로되어있냐 비선형으로 되어있냐를 의미하는 것이다.
  
  

머신러닝 규칙

1. 학습 상황에서 평가 데이터를 사용하면 안된다.
2. 학습 데이터 안에서는 y(라벨)를 모델에게 주면 안된다.
   • 머신은 라벨없이 학습을 진행하고, 인간은 머신의 output결과와 라벨을 비교 후 오류값을 머신에게 넘겨주고 머신을 업그레이드 하는 방식으로 동작한다.

출처
https://www.youtube.com/watch?v=oyzIT1g1Z3U&t=2621s