01. 최적화 이론 개요

• 걍 배운거 정리

최적화란? Optimization

Find an optimzation valiable that minimizes (or maximizes) an objective function possible given constraints(s)

• 목적 함수를 최소화 혹은 최대화 하는 최적화 변수를 찾는 과정이라고 한다.
• 이러저러한 역사 이야기는 skip...

Gauss's problem

위의 식을 아래의 식들로 표현

해당 문제들을 "least-squares" problem 이라한다고 한다.

아래의 특징을 지닌다

• Closed-form solution: $x^* = (A^TA)^-1A^Tb$
• Efficient method to compute the solution (솔루션을 계산하기에 효과적인 메소드)

그래서 ...

• Tired to translate an interested problem to a least-squares problem
• However: Encountered many situations in which translation is not doable

Linear Program

• WW2 때 나온 개념
• to solve a military-related problem during WW2
• Find Optimal planning of expenditures-returns of soldiers (지출-비용 문제)
• No closed form solution for LP.

Recall definition

• find optiomaztion variable that minimize (or maximize)
• an objective function
• possible given constraints(s)

Optimazation variable: $x \in R^d$
Objective function: $f(x) \in R$
Inequality constraint: $f_i(x) \leq 0_i \ \ \ \ i=1, ..., m$
Equality contraint: $h_i(x)=0 \ \ \ \ i=1,...,p$

위의 정의를 아래의 식처럼 표현할 수 있다

$x$ : Optimal point(?)
$p$ : Optimal value

Convex set

• Definition : A set S is said to be convex if ...
• 아래식 만족하면 convex set이다
  $x,y \in S \Rightarrow \lambda x + (1-\lambda)y \in S \ \ \ \ \nabla \lambda \in [0,1]$

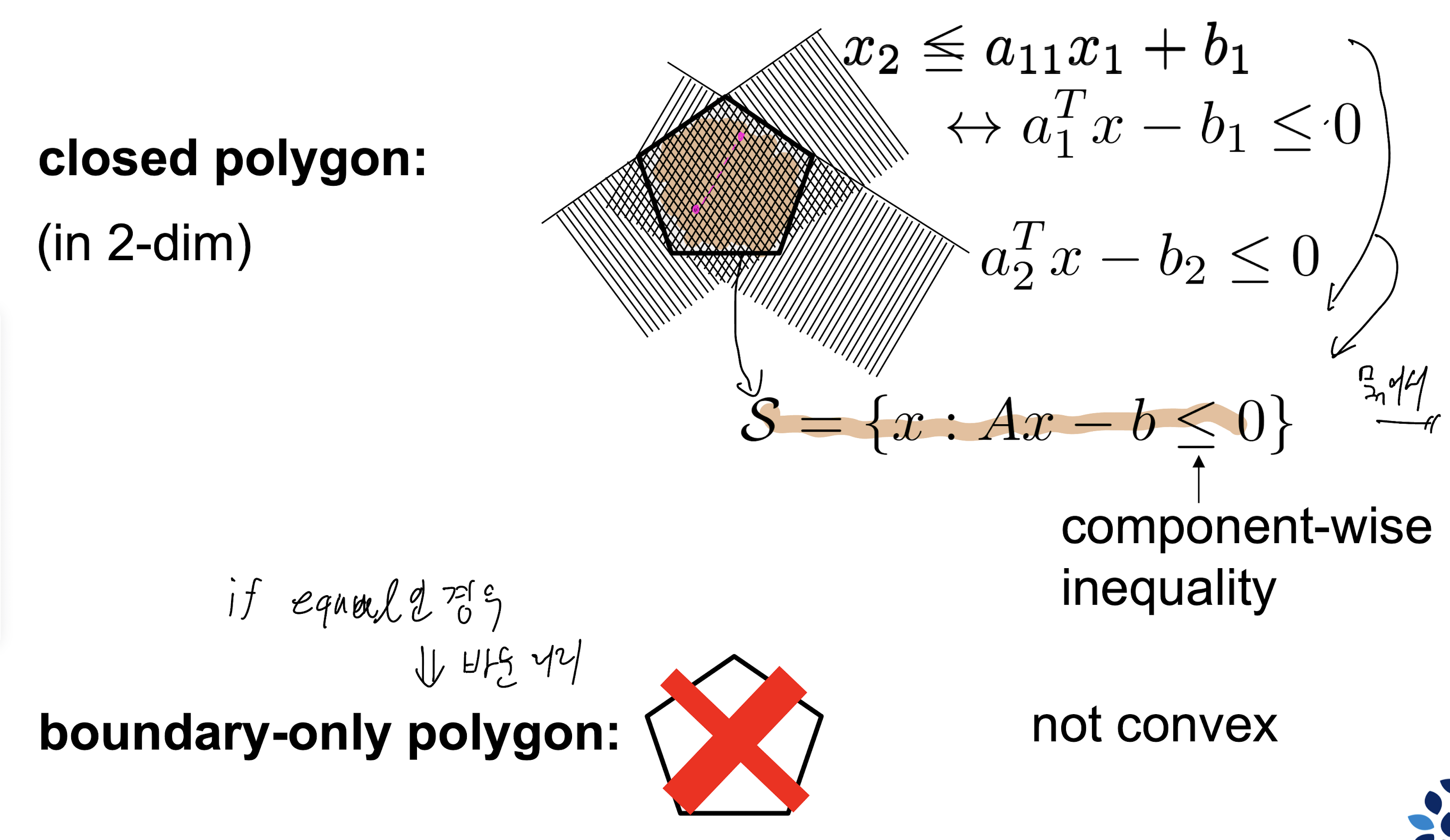
• 차원이 달라져도 표현은 같다.
  $S={x:Ax-b \leq 0}$

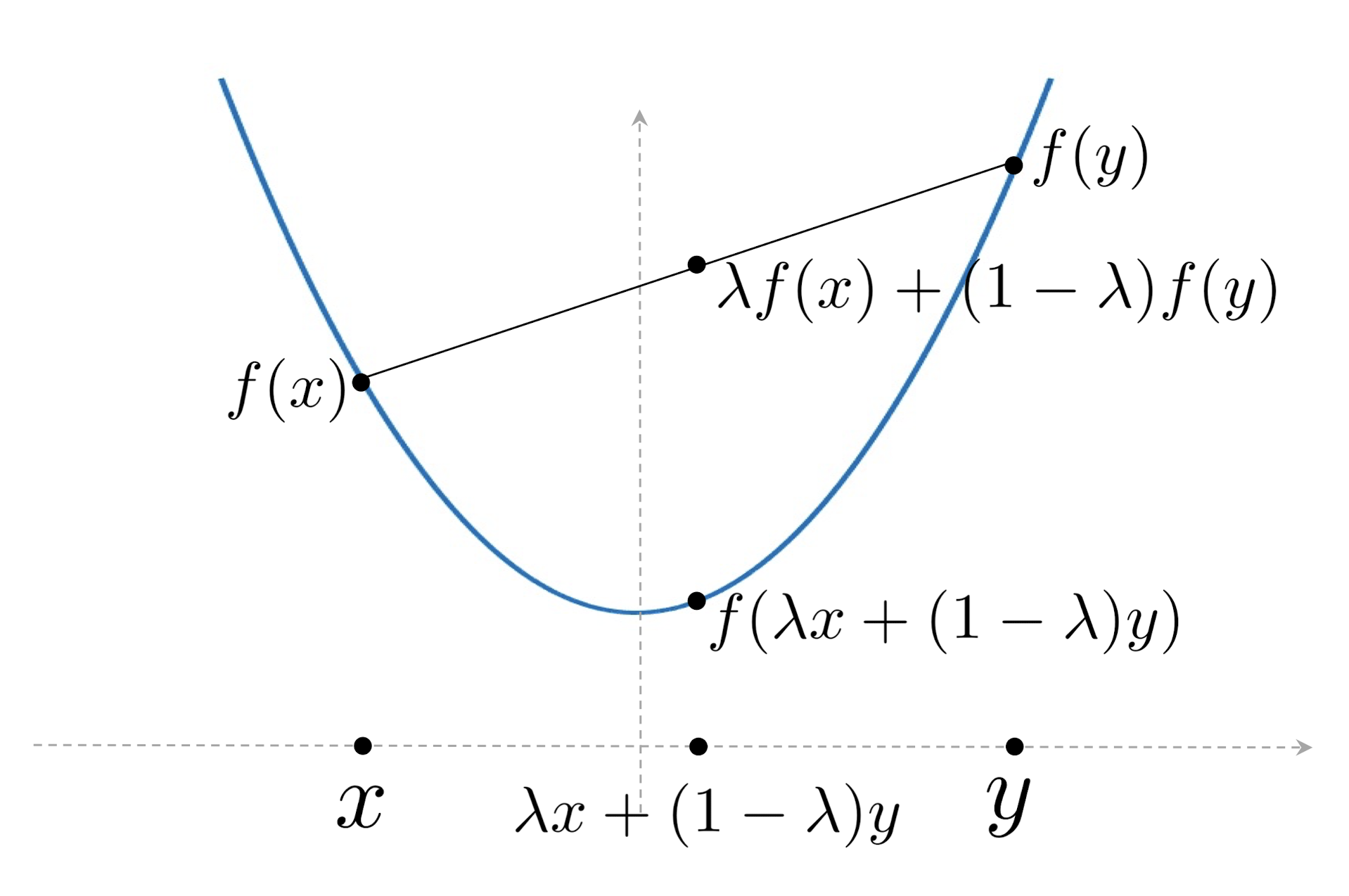
Convex function

1. $x,y \in domf: \ \ \ \ \ \forall \lambda \in [0,1]$
2. $dom f convex set

• convex means bowl-shaped
  
  

Concave

• $f(x)$ is concave if $-f(x)$ is convex

Affine

• $f(x)$ is affine if it is convex & concave

Convex Optimazation

• Object function is convex
• the set induced by inequality constraints is convex
• the set induced by equality constraints is convex