[부스트캠프 AI Tech] U-stage. 3-1

느린 개발자·2021년 2월 1일

부스트캠프

부스트캠프 AI Tech

목록 보기

12/35

📌 Bayesian Statistics

데이터가 새로 추가되었을 때, 정보 또는 모수(Parameter)를 업데이트 하는 방식 에 기반이 되는 베이즈 정리를 살펴보도록 한다.

📄 조건부 확률

조건부 확률 $P(A|B)$ 는 사건 B가 일어난 상황에서 사건 A가 발생할 확률 이다.

P(A|B)=\frac{P(A\cap B)}{P(B)}

📄 전 확률의 법칙(Law Of Total Probablity)

표본공간 $S$ 를 4개의 사건 $B_1,B_2,B_3,B_4$ 로 나눠져있다고 가정하자.

이때, 나눠진 4개의 영역을 포함하는 표본공간 S의 사건 A 를 생각해본다면 다음과 같다.

따라서 사건 A는 다음과 같이 나타낼 수 있다.

P(A)=\sum^4_{i=1}P(A\cap B_i)=\sum^4_{i=1}P(B_i)P(A|B_i)

📄 베이즈 정리(Bayes' Theorem)

베이즈 정리는 두 확률변수의 사전확률 과 사후확률 사이의 관계를 나타내는 정리 로 조건부확률을 이용하여 새로운 데이터에 대한 정보를 갱신하는 방법을 알려준다. 즉, 사전확률을 기반으로 새로운 추가 정보를 바탕으로 신뢰도를 갱신해나가는 귀납적 추론 방법이다.

✏️ Posterior / Prior / Likelihood / Evidence

Evidence : 새롭게 관측된 데이터 또는 증거.
Posterior : Evidence를 관측한 후 모델에 대한 확률.
Prior : Evidence를 관측 하기전 시스템 또는 모델에 대해 가지고 있는 선험적 확률.
Likelihood : 어떤 모델에서 evidence 가 표현될 가능성.

✏️ 예제

Problem:
COVID-19 의 발병률이 10% 로 알려져 있다. COVID-19 에 실제로 걸렸을때 검진될 확률은 99% , 실제로 걸리지 않았을 때 오검진될 확률이 1% 라고 할때, 어떤 사람이 질병에 걸렸다고 검진결과가 나왔을 때 정말로 COVID-19 에 감염되었을 확률은 무엇인가?

Solution:
우선 $D$ =검진결과 , $\theta$ =COVID-19 발병 으로 정의한다. 그러면 사전확률(Prior) $P(\theta)=0.1$ , 가능도(Likelihood) $P(D|\theta)=0.99, P(D|ㄱ\theta)=0.01$ 이다. 또한 LOTP(Law Of Total Probablity)에 의해 $P(D)=\sum_\theta P(\theta)P(D|\theta)=0.99*0.1+0.01*0.9=0.108$ 이다.
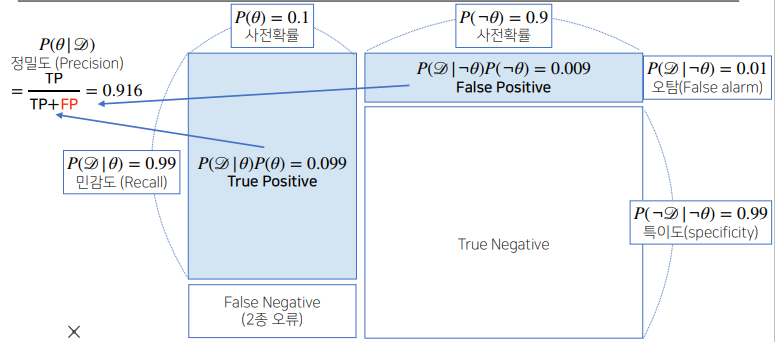
따라서 사후확률(Posterior) $P(\theta|D)=P(\theta)\frac{P(D|\theta)}{P(D)}=0.1\times\frac{0.99}{0.108}\approx 0.916$ 이다.

✏️ 평가 척도

용어	의미
TP(True Positive)	양성으로 예측했을 때, 실제로 양성인 수.
TN(True Negative)	음성으로 예측했을 때, 실제로 음성인 수.
FP(False Positive)	양성으로 예측했을 때, 실제로 음인일 수.
FN(True Negative)	음성으로 예측했을 때, 실제로 양성인 수.
False Alarm(오탐)	음성환자 중 양성으로 판단한 수.
Recall(민감도)	양성환자 중 양성으로 판단한 비율.
Specificity(특이도)	음성환자 중 음성으로 판단한 비율.
Precision(정밀도)	양성으로 예측한것 중 실제 양성인 비율.
Accuracy(정확도)	전체 환자 중 양성과 음성을 판단한 비율.

오탐
만약 오탐의 값이 커지게 되면 다음과 같이 정밀도가 떨어지게 된다.
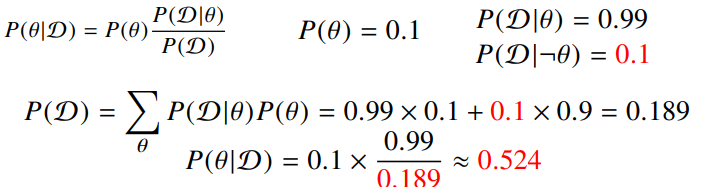
1종오류 / 2종 오류
다루는 문제에 따라 1종오류와 2종오류의 중요성이 달라지게 된다. 예를들어, 암환자를 진단하는 문제의 경우 암이 아니라고 판단하였으나 실제로 암인 경우(2종오류) 가 암이라고 판단하였으나 실제로 암이 아닌 경우(1종오류) 보다 더 심각한 문제이므로 2종오류를 줄이는 방향으로 접근하게 된다.

✏️ 정보의 갱신

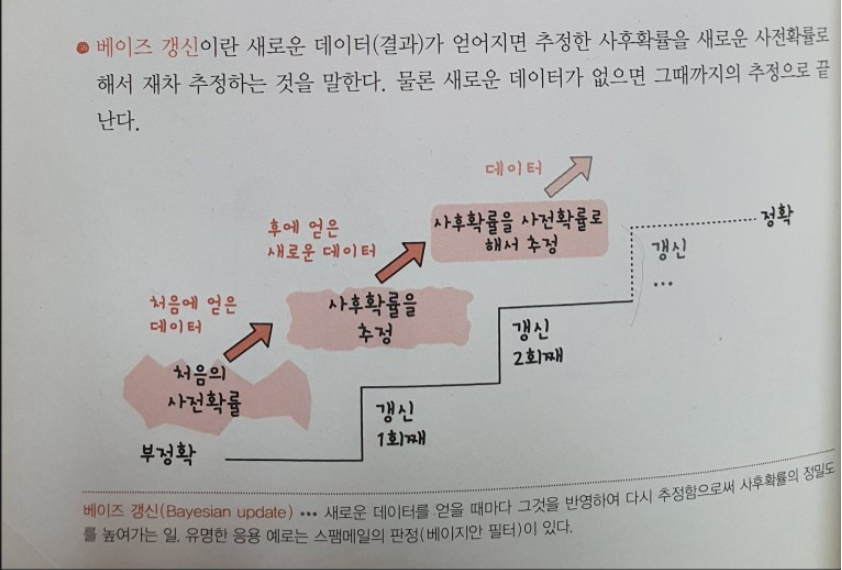
베이즈 정리가 주는 의의는 새로운 데이터가 들어왔을때, 앞서 계산한 사후확률을 사전확률로 사용하여 갱신된 사후확률을 계산할수 있다는 것이다.

✏️ 예제

Problem:
앞서 COVID-19 판정을 받은 사람이 두번 째 검진을 받았을 때도 양성이 나왔을 때 진짜 COVID-19에 걸렸을 확률 은 무엇인가?

Solution:
앞서 구한 사후확률 $P(\theta|D)=0.916$ 는 새로운 $D^\ast$ 에 대한 사전확률(Prior) $P(\theta)=0.916$ 이 된다. 그래서 $P(D^\ast)=0.99*\textcolor{red}{0.916}+0.1*\textcolor{red}{0.084}\approx0.917$ 가 된다.
, 가능도(Likelihood) $P(D|\theta)=0.99, P(D|ㄱ\theta)=0.01$ 이다. 또한 LOTP(Law Of Total Probablity)에 의해 $P(D)=\sum_\theta P(\theta)P(D|\theta)=0.99*0.1+0.01*0.9=0.108$ 이다.
따라서 사후확률(Posterior) $P(\theta|D)=P(\theta)\frac{P(D|\theta)}{P(D)}=0.1\times\frac{0.99}{0.108}\approx 0.916$ 이다.

📄 조건부확률은 인과관계(Causality)를 의미하나요?

흔히 조건부확률을 인과관계(Causality)로 추론하는 오류를 범하는 경우가 있는데, 조건부확률만을 가지고 인과관계를 추론하는 것은 불가능하다. 이것에 대한 이해는 상관관계(Correlation) 와 인과관계(Causality)의 정확한 차이를 직관적으로 파악해야 할 필요가 있다.

상관관계
예를 들면, 아이스크림 소비량과 익사사고 발생률을 비교해보면, 아이스크림 소비량이 높을수록 익사사고 발생률이 높다는 것을 알 수 있다. (둘 다 여름에 높아지기 때문이다.) 이러한 관계를 양의 상관관계가 있다고 한다. 그렇다면, 아이스크림을 못사게하면, 익사사고 발생률을 낮출 수 있을까? 당연히 아닐것이다. 그 이유는 아이스크림 소비량과 익사사고 발생률은 인과관계가 없기 때문이다.
인과관계
예를 들면 , 기온과 아이스크림 소비량은 인과관계를 가질수 있다. 기온의 상승이 아이스크림 소비량을 늘릴 수 있기 때문입니다. 반대로 기온이 낮으면 아이스크림 소비량이 감소할 수 있다.

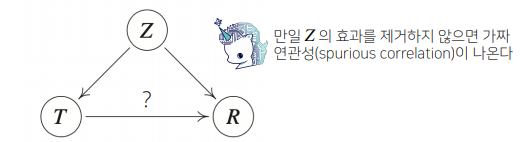
인과관계는 데이터 분포의 변화에 강건한 예측모형 을 만들때 필요하다. 그렇다면 어떻게 조건부확률을 오류를 범하지 않고 유용한 통계적 해석을 이끌어 낼 수 있을까? 이에 대한 답은 중첩요인(Confounding factor)의 효과를 제거하고 원인에 해당하는 변수만의 인과관계를 계산해야 한다.

✏️ 예제(Simpson's Paradox)

심슨의 역설(Simpson's Paradox) 이란 $\frac{a_1}{A_1}>\frac{b_1}{B_1}$ 이고 $\frac{a_2}{A_2}>\frac{b_2}{B_2}$ 라고 반드시 $\frac{a_1+a+2}{A_1+A_2} > \frac{b_1+b_2}{B_1+B_2}$ 인것은 아님을 말한다. 즉, 각 부분에 대한 평균이 크다고 해서 전체에 대한 평균까지 크지는 않다는 의미이다.

치료법 a 의 경우 작은 결석, 큰 결석 치료에 치료법 b보다 높은 성공률을 보였으나, 전체 그룹으로 보았을땐 치료법 b의 성공률이 치료법 a 보다 높은것을 볼 수 있다. 즉, 그룹을 나누어서 봤을 때 나타나는 현상이 그룹을 합쳤을때는 사라지거나 오히려 경향이 역전되었다.

이런 현상이 나타나는 이유를 생각해본다면, 치료법 a는 큰 결석크기를 갖고 있는 환자가 많이 받았고, 치료법 b는 작은 결석 환자가 많이 받았다. 그래서 치료법 a는 대부분 치료가 어려운 환자를 상대했기 때문에 치료율이 낮을 수 밖에 없는것이다.

이를 변수를 도입하여 살펴본다면, 치료법= $\bold{T}$ ,결석크기= $\bold{Z}$ ,치료여부= $\bold{R}$ 에서 우리가 알고 싶어하는것은 $\bold{T}$ 와 $\bold{R}$ 과의 관계 이다. 그러나 $\bold{Z}$ 가 $\bold{T}$ , $\bold{Z}$ 모두 영향을 주면서 $\bold{T}$ 와 $\bold{R}$ 의 인과관계 판단에 영향을 준다. 이러한 변수 $\bold{Z}$ 를 혼란변수(Confounding Variable) 라 부른다.

그렇다면 어떻게 중첩요인을 제거하여 올바른 해석을 할 수 있을까?

IPW(Inverse Propensity Weighting) 을 이용하여 각 데이터에 가중치를 부여하여 그룹의 균형을 맞추도록 한다. 간단한 예로 이해를 돕자면, 총 5명의 성인 남성중 치료받은 1명의 성인 남성과 치료받지 못한 4명의 성인 남성이 있다고 가정한다. 각 그룹에선 남성의 분포가 다르기 때문에 다음과 같이 inverse weighting 을 통해 그룹의 분포를 균등하게 맞춰준다. 그 후 가중평균을 이용하여 판단하도록 한다.

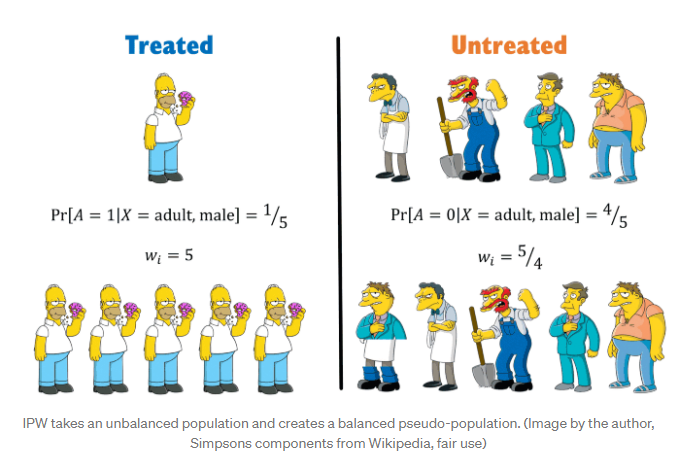
이를 바탕으로 예제에 적용해본다면, $Z=0$ 인 각 그룹(치료법a,치료법b)의 균등한 분포를 위해 $\frac{(270+87)}{87}$ 과 $\frac{(270+87)}{270}$ 가중치를 곱한다. $Z=1$ 인 분포에는 각 그룹에 $\frac{(263+80)}{263}$ 과 $\frac{(263+80)}{80}$ 가중치를 곱한다.

Treatment\ a:\ P_a(R=1)=\frac{\sum_{i\in\{0,1\}}P(R=1|T=a,Z=z)\cdot w_i}{\sum_{i\in\{0,1\}}w_i}

\Rightarrow P_a(R=1)=\frac{(\frac{81}{87}\textcolor{red}{\frac{(270+87)}{87}}+\frac{192}{263}\textcolor{red}{\frac{(263+80)}{263}})}{\textcolor{red}{\frac{(270+87)}{87}}+\textcolor{red}{\frac{(263+80)}{263}}}\approx88.26\%

Treatment\ b:\ P_b(R=1)=\frac{\sum_{i\in\{0,1\}}P(R=1|T=b,Z=z)\cdot w_i}{\sum_{i\in\{0,1\}}w_i}

\Rightarrow P_b(R=1)=\frac{(\frac{234}{270}\textcolor{red}{\frac{(270+87)}{270}}+\frac{55}{80}\textcolor{red}{\frac{(263+80)}{80}})}{\textcolor{red}{\frac{(270+87)}{270}}+\textcolor{red}{\frac{(263+80)}{80}}}\approx72.97\%

이 예제에선 그룹이 나뉘어진 데이터를 먼저 보았기 때문에 올바른 해석을 이끌어 낼 수 있었지만, 실제로 우리가 보는 데이터는 그룹별로 나뉘어진 데이터가 아닐 수 있기 때문에 잘못된 결론을 이끌어 낼 수 있다. 또한 중첩요인을 파악하여 정확한 인과관계를 추론하는 것이 강건한 예측모형을 만드는데 필요할 것이다.

📌DL Basic

DeepLearning 을 하기 위한 개발환경 셋팅과 Pytorch 와 MNIST 데이터를 활용하여 간단한 MLP 모델에 대해 살펴본다.

📄 구글 코랩과 VScode 연결

Cloudflared 를 운영체제 버전에 맞게 설치한다.
VScode extension에서 Remote - SSH 를 설치한다.

구글 코랩 으로 이동하여 노트설정 에서 GPU 설정하고 다음의 코드를 실행한다.

# Install colab_ssh on google colab
!pip install colab_ssh --upgrade

from colab_ssh import launch_ssh_cloudflared, init_git_cloudflared
launch_ssh_cloudflared(password="YOUR PASSWORD")

# Optional: if you want to clone a github repository
# init_git_cloudflared(githubRepositoryUrl)

VScode 에서 ctrl+shift+p 를 눌러 다음을 입력한 후 위의 configuration 을 붙여넣는다. 이때, <PUT_THE_ABSOLUTE_CLOUDFLARE_PATH_HERE> 부분은 위에서 설치한 cloudflared 실행파일이 있는 절대경로 를 적는다.

VScode 에서 ctrl+shift+p 를 눌러 다음을 입력한 후 위의 VSCode Remote SSH 정보를 붙여넣는다.

연결 플랫폼은 Linux 를 선택 후 launch_ssh_cloudflared(password='PASSWORD') 에서 설정한 password를 입력한다.
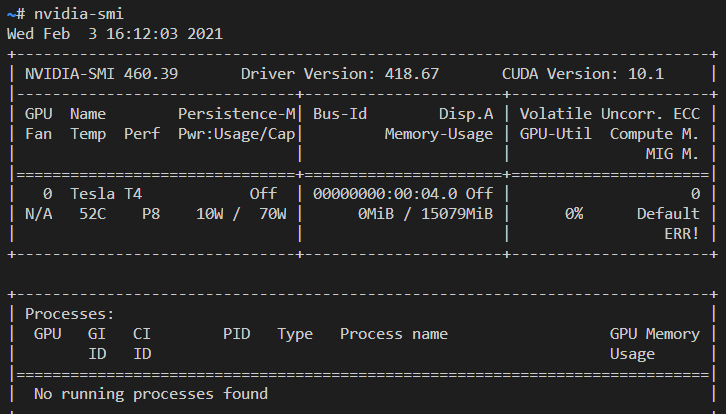
연결 후 VScode 에서 ctrl+shift+p 를 눌러 다음을 입력한 후 terminal 에서 nvidia-smi command를 사용할 수 있는 GPU를 확인해본다.