📌 DL Basics
최적화(Optimization)의 기본 concepts 과 다양한 method 들, 그리고 Generalization performance 를 높이기 위한 Regularization 들을 정리하고, CNN(Convolutional Neural Network) 의 베이스가 될 Convolution 연산에 대해 살펴 보도록 한다.
📌 Optimization
📄 Important Concepts
✏️ Generalization
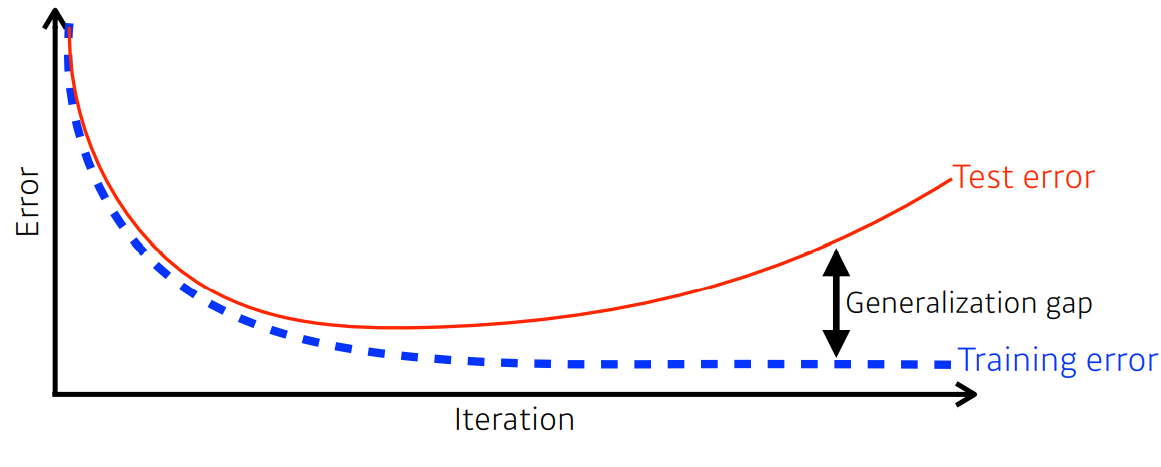
모델 학습을 잘 시켰다는 것은 학습 데이터 뿐만 아니라 새로운 데이터를 얼마나 잘 맞추는가? 를 말한다. 이것은 training error가 완전히 줄었다고 하더라도, 최적값에 도달했다고 말할수 없음을 의미한다. 그래서 우리의 주요 관심사는 training error를 줄임과 동시에 training error 와 test error 의 차이(Generalization gap) 또한 줄이는 것이 최종 학습 목표이다.
예를들어, 어떤 뉴럴넷이 generalization performance 가 높다는 것은 네트워크의 성능이 학습데이터에서의 성능과 비슷하게 나올것을 의미한다. 하지만 generalization performance가 높다는 것이 네트워크의 성능이 좋음을 의미하는건 아니다. 만약 학습데이터에서 성능이 안 좋으면 generalization performance가 높다 하더라도 테스트 데이터에서의 성능을 보장하는 것은 아니기 때문이다.
✏️ Under-fitting vs Over-fitting
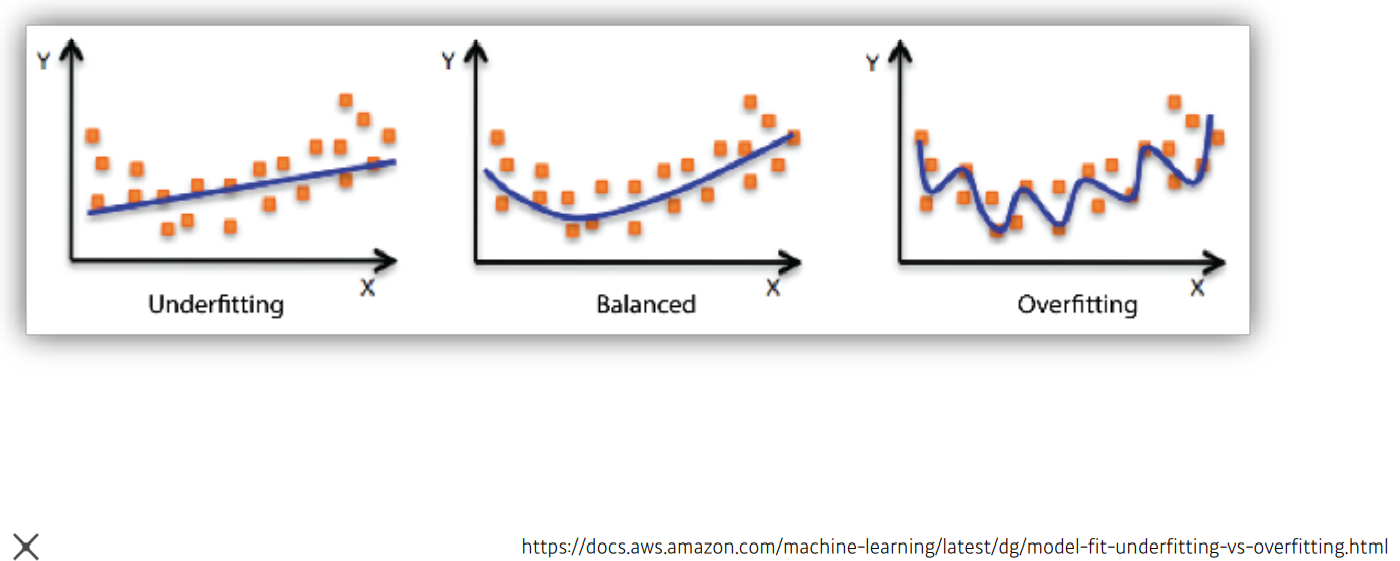
학습의 목표는 , 위에서 언급했듯이, 주어진 학습데이터로 일반적인 패턴을 발견하는 것이다. 가장 이상적인 방향은 balanced-fitting 과 동시에 generalization performance 를 높이는 것이다. 하지만, 실제 문제에서 balanced-fitting 은 쉽지 않은 일이며, 다음과 같은 문제가 발생할 수 있다.
-
Under-fitting
학습을 마친 후 모델의 성능이 기대치보다 떨어지는 현상 을 말한다. 즉, 이상적인 결정경계(Decision Boundary) 에 비해 지나치게 단순한 경우로 학습데이터 조차 제대로 학습하지 못한 상황이다. Under-fitting이 발생하는 이유는 다음과 같다.- 작은 학습 반복 횟수.
- 데이터의 feature에 비해 간단한 모델.
- 학습 데이터 부족.
-
Over-fitting
학습을 마친 후 새로운 데이터에 대해서는 그 결과가 매우 다르게 나오는 현상 을 말한다. 즉, 이상적인 결정경계보다 지나치게 복잡한 경우로 학습데이터에 과하게 학습된 상황이다. Over-fitting 이 발생하는 이유는 다음과 같다.- 편중된 학습데이터.
- 너무 많은 데이터 feature 로 모델이 복잡.
- 무분별한 noise 수용.
충분한 학습데이터 확보, 모델 및 하이퍼파라미터 조정 등을 통해 under-fitting / 다양한 학습데이터 확보, regularization 등을 통해 over-fitting 을 해결한다. 또한 under-fitting 과 over-fitting은 trade-off 관계를 가지므로 적절한 파라미터 설정이 중요하다.
✏️ Bias and Variance Tradeoff

모델을 학습한다는 것은 cost 를 최소화하는것이다. 위의 식과 같이 cost 를 최소화하는 것은 bias 와 variance를 조절하는 문제로 바라볼 수 있으며, (Noise는 데이터가 가지는 본질적인 한계치 이기 때문에 irreducible error, bias/variance 는 모델에 따라 변하는 것이기에 reducible error) bias / variance 는 trade-off 관계를 가지므로 적절한 파라미터 설정이 주요문제 임을 확인할 수 있다.
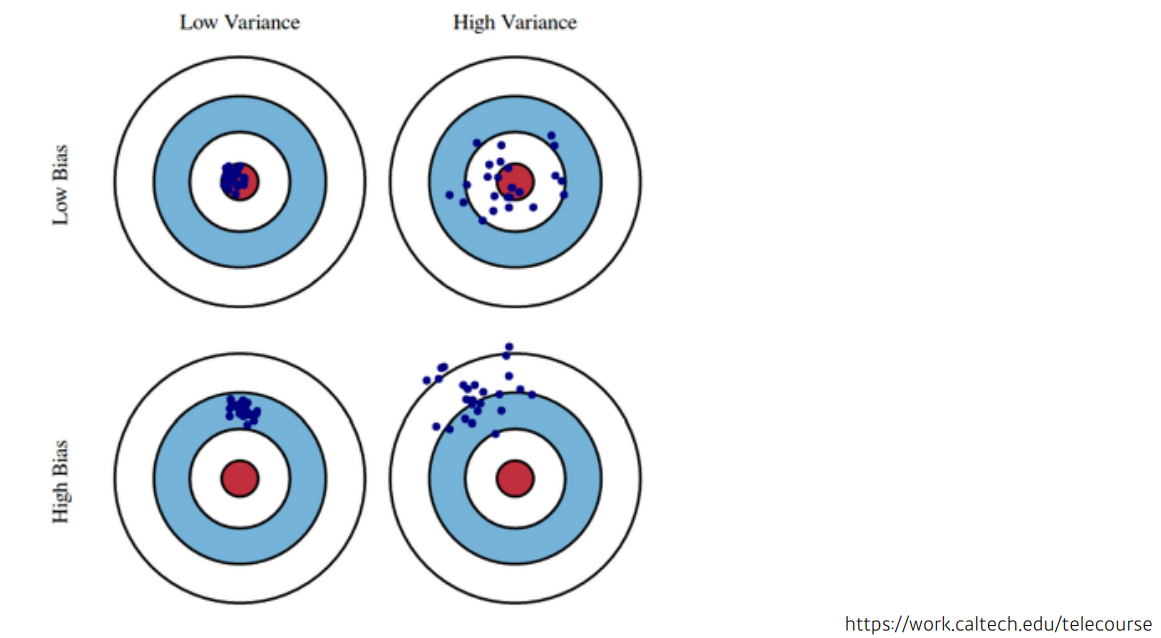
Bias 는 학습된 모델과 실제 값 사이의 에러를 나타내는 척도이며, Variance 는 학습된 모델이 새로운 데이터 셋에 성능의 변화정도가 얼마나 안정적인지를 나타내는 척도이다.
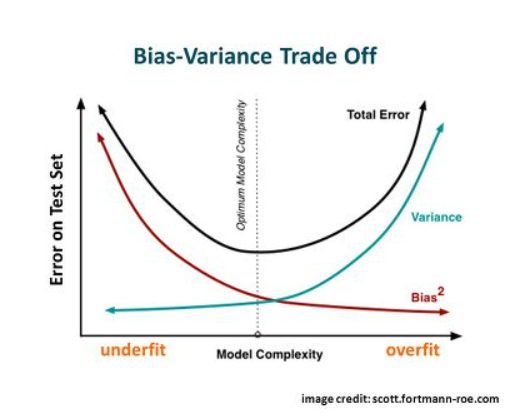
- High bias & Low variance (Under-fitting)
새로운 데이터가 들어와도 성능의 변화 없이 안정적인 결과를 낸다.(Low variance) 하지만 학습을 너무 rough하게 하여 애초에 모델성능이 좋지 않은 경우이다.(High bias)
- High variance & Low bias (Over-fitting)
주어진 학습데이터를 잘 설명하고 있다.(Low bias) 하지만 모델을 너무 tight하게 학습하여 데이터가 조금만 변해도(ex 노이즈) 모델이 매우 다른 결과를 내는 경우이다.(High variance)
✏️ Cross-validation
우리가 사용할 데이터가 train dataset 과 test dataset으로 구성되어 있다고 가정하자. 만약 train dataset을 train dataset + validation dataset 으로 나누지 않는다면 test dataset을 validation dataset으로 사용하여야 한다.(Validation vs Test) 그런데 고정된 test dataset을 validation dataset으로 사용하여 파라미터를 수정하는 행위는 결국 test dataset을 학습에 이용하진 않았지만 직접 살펴보고 학습한 결과를 이끌어 over-fitting 이 되는 문제가 생긴다.
이 문제를 해결할 수 있는 방법은 validation set 을 일부분으로 고정 시키지 않고 데이터의 모든 부분을 사용하여 모델을 검증하는 것이다. 이러한 방식을 교차검증(Cross-validation)이라 하며, 다음과 같은 특징을 가진다.
-
모든 데이터 셋을 평가에 활용할 수 있다.
-
Over-fitting 을 예방할 수 있다.
-
Generalization performance를 높일 수 있다.
-
-
모든 데이터 셋을 훈련에 활용할 수 있다.
-
정확도를 향상시킬 수 있다.
-
데이터 부족으로 인한 underfitting을 방지할 수 있다.
-
다음은 대표적인 교차검증 방법들이다.
- K-fold Cross-validation
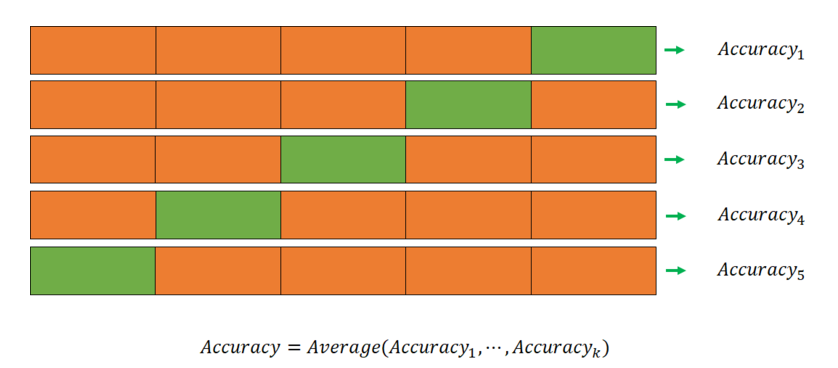
가장 일반적으로 사용되는 교차검증방법으로, 데이터를 K개의 fold로 분할하여 각 iteration 마다 K-1개의 training folds 와 1개의 validation fold을 다르게 두어 훈련 및 검증한다. 따라서 총 K번의 iteration이 필요하며, 검증결과들을 평균내어 최종 검증결과를 도출한다.
from sklearn.model_selection import KFold
import numpy as np
data=np.arange(0.,1.,0.1)
kf=KFold(n_splits=5) # K=5 , fold 당 2개
for idx,(train,valid) in enumerate(kf.split(data)):
print(f' Iteration [{idx+1}] Train set : {data[train]} Validation set : {data[valid]}')
- Hold-out Validation

주어진 train dataset을 임의의 비율로 train : validation 으로 분할 하여 사용한다. 훈련 및 검증을 단 한번만 하기 때문에 계산 시간에 부담이 적으나, **고정된 validation set으로 검증결과 확인 후 모델파라미터 튜닝을 반복하게 되면 over-fitting 될 가능성이 높다
from sklearn.model_selection import train_test_split
import numpy as np
data=np.array([0.1,0.2,0.3,0.4,0.5,0.6])
train,test=train_test_split(data, random_state=3, test_size=0.3)
print(f'Train set : {train} Validation set : {test} ')
- Leave-p-out Cross-validation

전체 데이터 중에서 p개의 샘플을 뽑아 validation dataset으로 하여 훈련 및 검증한다. 따라서 만큼 iteration을 반복한다.
from sklearn.model_selection import LeavePOut
import numpy as np
data=np.array([0.1,0.2,0.3,0.4,0.5,0.6],dtype=np.float32)
lpo=LeavePOut(p=2) # 6C2 = 15 iterations
for idx,(train,valid) in enumerate(lpo.split(data)):
print(f' Iteration [{idx+1}] Train set : {data[train]} Validation set : {data[valid]}')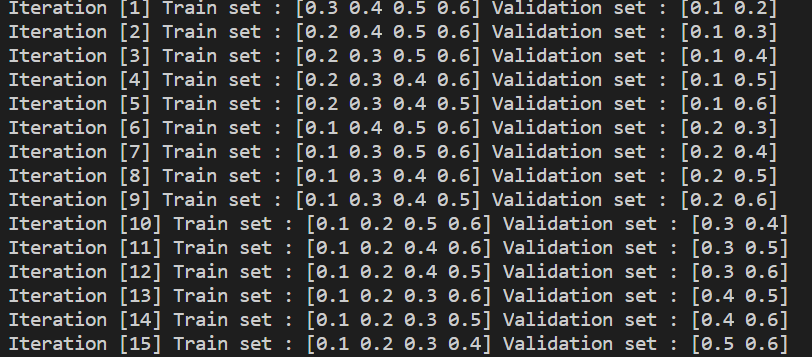
- Leave-one-out Cross-validation

Leave-p-out Cross-validation에서 p=1인 경우 로 검증에 사용되는 데이터가 적은 만큼 모델 훈련에 사용되는 데이터가 늘어난다. 모델 검증에 사용되는 데이터의 갯수가 단 하나이기 때문에 나머지 모든 데이터를 훈련에 사용할 수 있다는 것이 특징이다.
from sklearn.model_selection import LeaveOneOut
import numpy as np
data=np.array([0.1,0.2,0.3,0.4,0.5,0.6])
l1o=LeaveOneOut() # 6C1 = 6 iterations
for idx,(train,valid) in enumerate(l1o.split(data)):
print(f' Iteration [{idx+1}] Train set : {data[train]} Validation set : {data[valid]}')

- Stratified K-fold Cross-validation
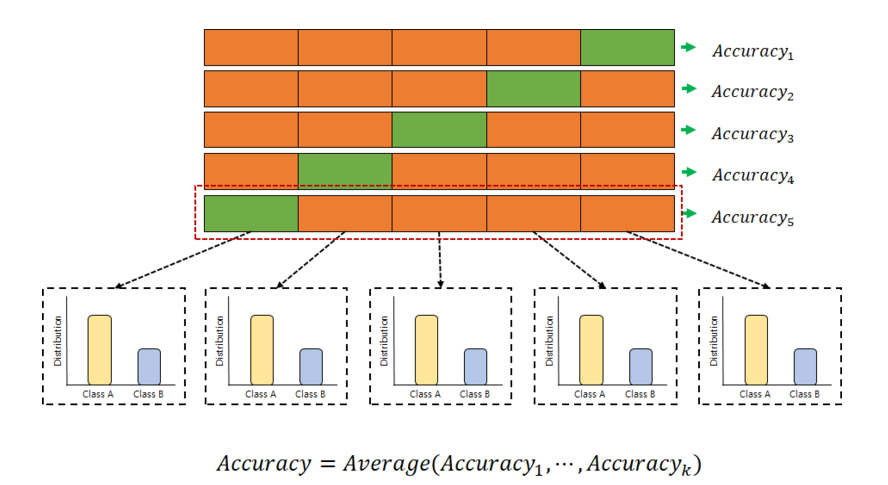
데이터 label의 분포까지 고려하여 각 폴드의 라벨분포가 전체 데이터의 라벨분포에 근사하여 훈련 및 검증한다. label의 분포가 불균형한 상태로 검증하는 것은 오류를 일으킬수 있으므로 주로 classification 문제에서 사용된다.
from sklearn.model_selection import StratifiedKFold
import numpy as np
data = np.array([0.1, 0.2, 0.3, 0.4, 0.5, 0.6])
y = np.array([1,1,0,1,1,0])
skf = StratifiedKFold(n_splits = 2, shuffle=True) # k=2 -> fold 당 3개
for idx,(train, valid) in enumerate(skf.split(data, y)):
print(f' Iteration [{idx+1}] Train set : ({data[train]} / y : {y[train]}) Validation set : ({data[valid]} / y: {y[valid]})')
- Shuffle-split Cross-validation
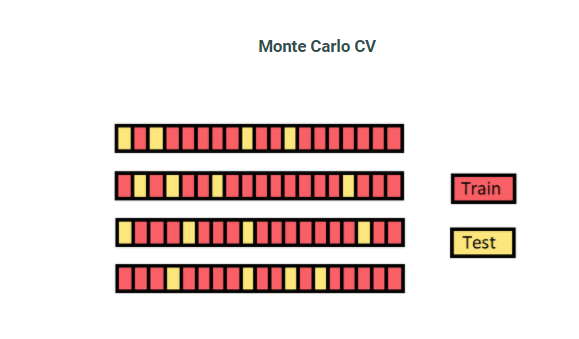
train dataset과 test dataset을 랜덤하게 나누고 반복 한다. 이 방법의 문제는 랜덤하게 나누어 지므로 어떤 fold 는 여러 번 선택 되는 반면 한번도 선택되지 못한 fold 가 생길 수 있다.
from sklearn.model_selection import ShuffleSplit
import numpy as np
data = np.array([0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9])
shuffle = ShuffleSplit(n_splits=5, test_size=0.2, random_state=42) # K=5
for idx,(train, valid) in enumerate(shuffle.split(data)):
print(f' Iteration [{idx+1}] Train set : {data[train]} Validation set : {data[valid]} ')
- Nested Cross-validation
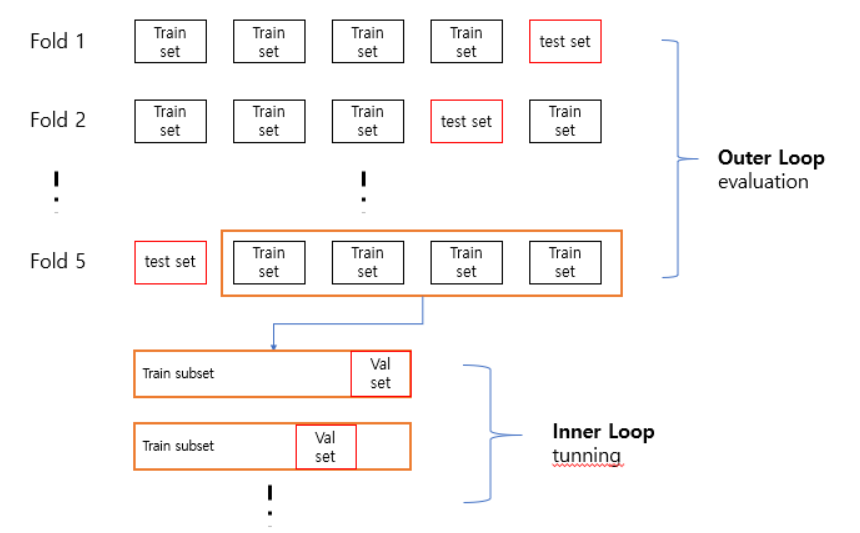
기존의 교차검증을 중첩한 방법으로 Outer loop 에서는 기존에 validation set을 나누는 것 대신에 test set을 다양한 fold 로 나누어 구성한다. Outer loop에서 생성된 train set 과 test set 중 train set에 대해서 inner loop를 적용하여 train set + validation set 으로 나누어 검증하고 파라미터 튜닝을 한다. 그 후 최적의 파라미터를 통해 outerloop에서 생성된 test set으로 평가하는 방식이다.
- Time-series Cross-validation
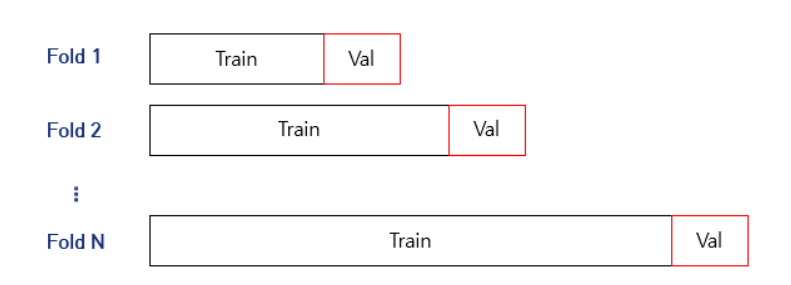
일반적인 데이터가 아닌 시계열 데이터의 경우 시간정보가 결과에 영향을 끼친다. 예를 들어, train set에 13시 데이터가 존재하고 validation / test set 에 14시 데이터가 존재한다면 유사 데이터를 학습하였기 때문에 성능이 좋은걸로 판단될 것이다. 그러나 새로운 아주 먼 미래의 데이터가 들어온다면 성능이 좋지 않을 것이다. 즉 High variance를 띄게 되고 over-fitting 이 발생할 것이다. 그래서 over-fitting 을 피하기 위해선 validation / test set에는 train set 보다 미래 데이터를 사용하는 것이 합리적인 검증 방법일 것이다.
from sklearn.model_selection import TimeSeriesSplit
data = np.array([0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9])
tsp=TimeSeriesSplit(n_splits=5)
for idx,(train, valid) in enumerate(tsp.split(data)):
print(f' Iteration [{idx+1}] Train set : {data[train]} Validation set : {data[valid]} ')
✏️ Bootstrapping
bootstrapping 은 고정된 데이터에 대해 random sampling with replacement를 적용하여 생성된 데이터 또는 이 데이터를 기반으로 만들어진 model / metric 을 생성하는것을 의미한다.
✏️ Bagging and Boosting
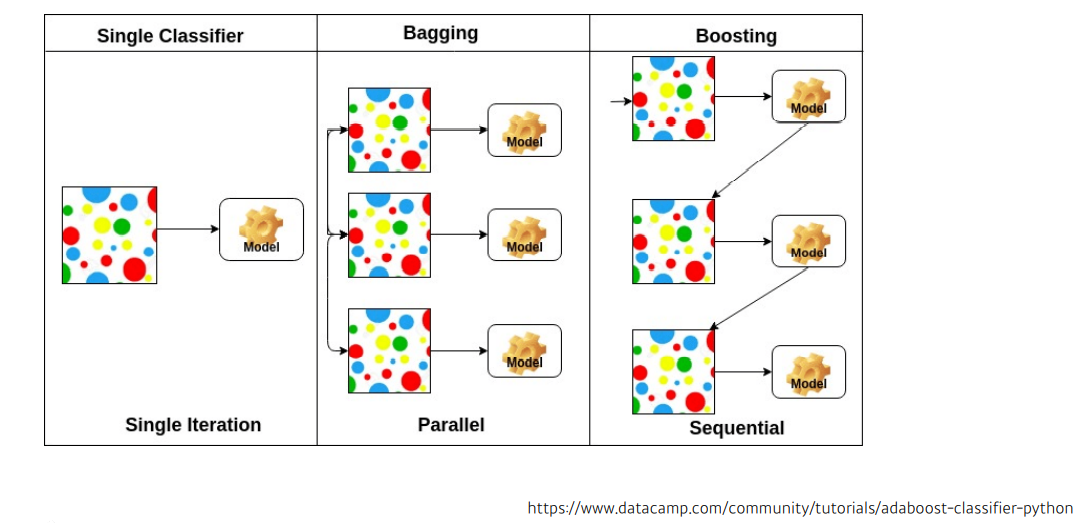
- Bagging(Bootstrap aggregating)
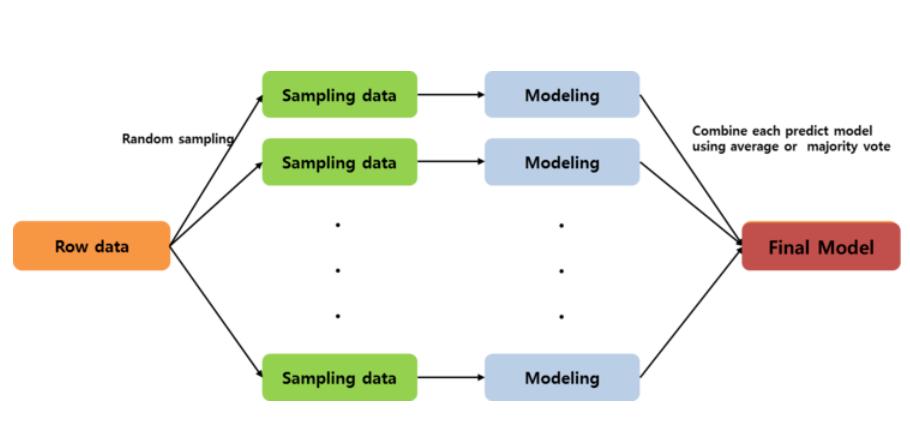
주어진 데이터에서 여러 개의 boostrap 을 이용하여 각각의 모델 생성 후 최종 모델을 결정하는 방법이다. 일반적으로 예측 모형의 변동성이 큰 경우 (High variance) 변동성을 감소시키기 위해 사용된다. 즉, 데이터로 부터 여러번의 복원 샘플링을 통해서 예측 모형의 분산을 줄여 줌으로써 예측력을 향상시키는 방법론을 bagging 이라 한다. 그래서 bagging은 High variance,Low bias(Over-fitting) 인 모델에 사용된다.
- Boosting
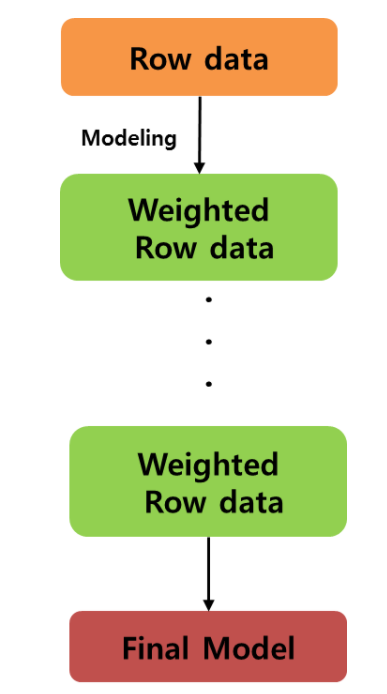
우리의 목적은 잘못 분류 / 예측된 개체들에 관심을 가지고 이들을 더 잘 분류 / 예측 하는 것이다. 그래서 잘못 분류된 개체들에 집중하여 새로운 분류 / 예측 규칙을 만드는 단계를 반복하는게 필요하였다. 즉, 약한 예측 모형들을 결합하여 강한 예측 모형을 만드는 것이 boosting 이다. boosting의 초점은 순차적으로 오분류된 개체들에게는 높은 가중치를 / 정확하게 분류된 개체들에게는 낮은 가중치를 적용하여 오분류된 객체들이 더 잘 분류되도록 하는 것이다.
📄 Methods
Neural network 는 Gradient Descent 를 기반으로 weight를 업데이트 한다. 그러나 기존에 쓰이던 Gradient Descent(Stochastic Gradient Descent) 만으로는 네트워크를 학습시키는데 한계가 있다. 그래서 다음에서 이것을 극복할 다양한 SGD의 변형 알고리즘들을 살펴 보도록 한다.
✏️ Batch-size
Gradient Descent 에서 batch-size 는 학습과 성능에 많은 영향을 끼친다. 그 중 generalization 에 대해 살펴보면, On Large-Batch Training for Deep Learning: Generalization Gap and Sharp Minima,2017 은 batch-size 가 클수록 sharp minimum에 도달하여 generalization gap이 커지고, 작을 수록 flat minimum에 도달하여 generalization gap이 줄어든다고 한다.
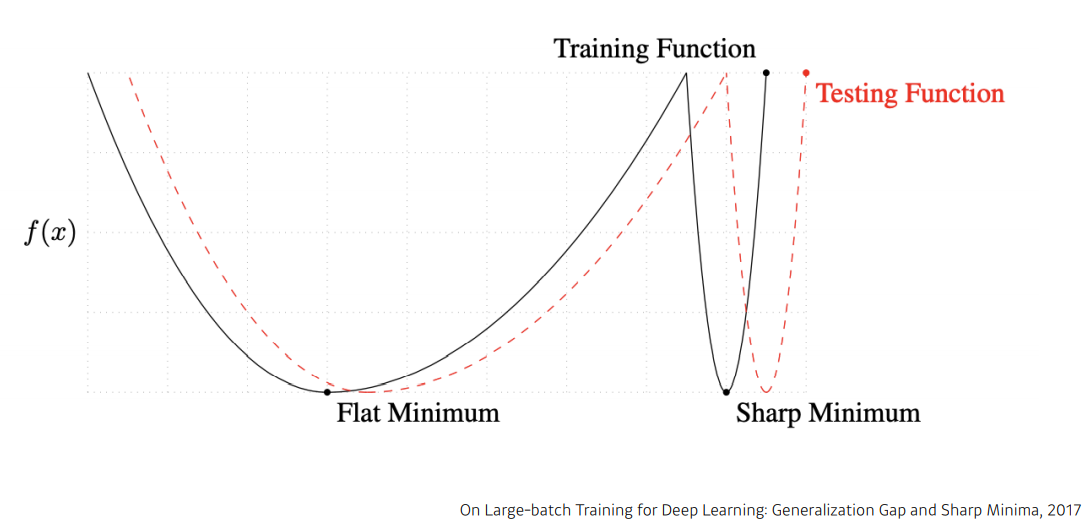
<참고>
(Accurate,Large Minibatch SGD: Training ImageNet in 1 Hour ,2017 은 자신들의 방법대로 학습하면 batch-size 를 8K까지 늘려도 일반화 성능의 하락이 관측되지 않았고, 더 나아가 Large Batch Training Of Convolutional Networks ,2017 은 자신들의 방법을 이용하면 Resnet-50 을 이용했을 때 32K까지 배치 사이즈를 늘려서 학습해도 정확도가 떨어지지 않는다고 주장하였다.)
정리해보면, batch-size 가 generalization에 영향을 끼치고 batch-size가 커지면 generalization gap 이 커지는 문제가 생긴다는 것이다. 그런데 실전에서는 batch-size를 메모리에 올라갈 수 있는 최대 크기로 설정하는 경우가 많은데, 이는 작은 batch-size로 업데 이트를 하는것보다 병렬화 하기 쉬워 계산비용을 절약할 수 있기 때문이라고 한다. 또한 위에서 언급한 논문들은 32~512 batch-size 를 넘어선 경우에 대해서 다루고 있기 때문에, 메모리에 올라갈수 있는한 최대한 크게 설정하는 것이다. 물론 학습이 잘 안되거나 모델 성능이 나오지 않은 경우에는 batch-size 역시 주의 깊게 설정해야 할 것이다.
✏️ Momentum
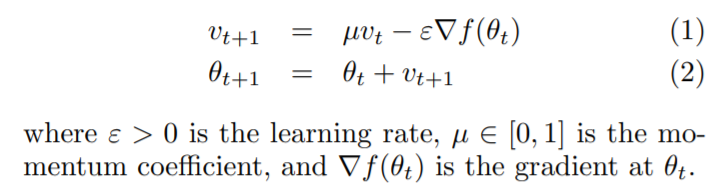
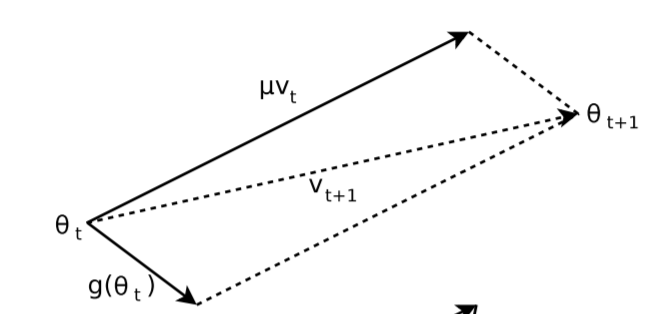
이름에서 알 수 있듯이, 기존의 Gradient Descent를 통해 파라미터 업데이트 과정에 일종의 Momentum(관성) 을 주는 것이다. On the importance of initialization and momentum in deep learning, 2013 에 따르면 과거의 누적 gradient (Accumulation) 에 momentum 을 곱한 momentum step 을 이용하여 현재 gradient 를 조정한다. 이때, 보통 모멘텀 을 사용한다
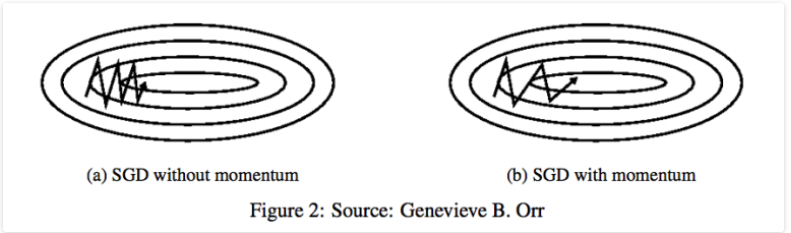
Momentum 방식은 SGD가 Oscilation(진동)을 겪을 때, 중앙의 최적점으로 이동하는 힘을 주어 SGD에 비해 상대적으로 빠르게 이동할 수 있다.
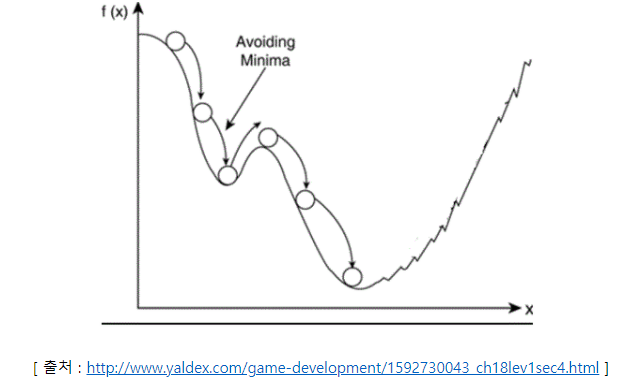
또한, local minima를 빠져나오는 효과를 기대해 볼수도 있는데, 기존에 이동했던 방향에 모멘텀이 있기 때문이다.
✏️ Nesterov Accelerated Gradient(NAG)
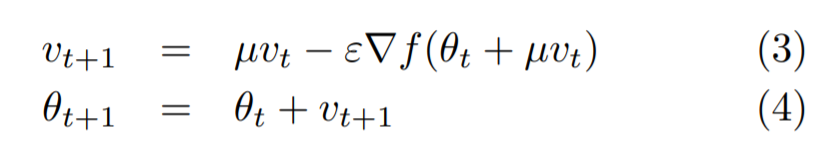
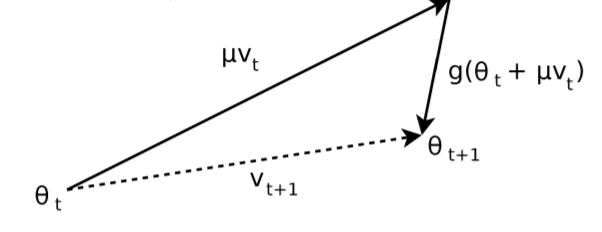
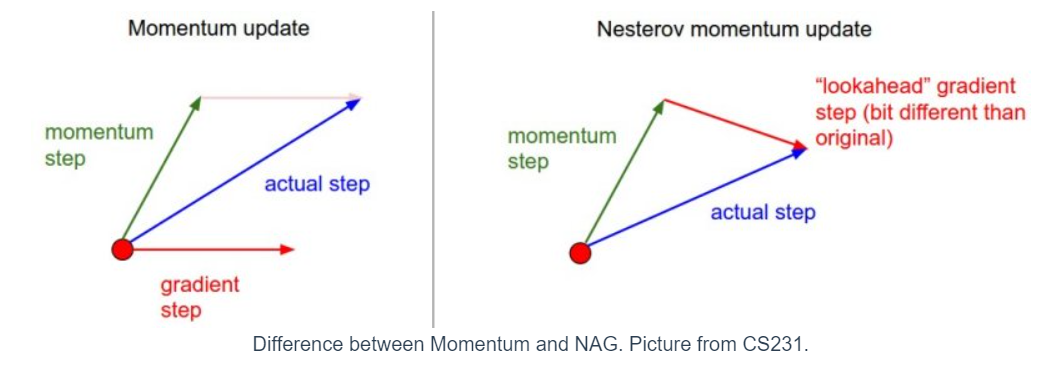
Momentum 방식을 기초로 하였지만, 현재 위치의 gradient 가 아닌 현재 위치에서 만큼 이동한 gradient 를 이용한다. 즉, 먼저 momentum step 을 적용한 위치에서의 gradient ("lookahead" gradient step) 를 구한 후 업데이트 한다.
NAG를 이용할 경우 기존의 Momentum 방식에 비해 효과적인데, lookahead gradient step 을 통해 어떤 방식으로 이동할지를 결정하므로 유동적인 이동이 가능하기 때문이다.
✏️ Adagrad(Adaptive Gradient)
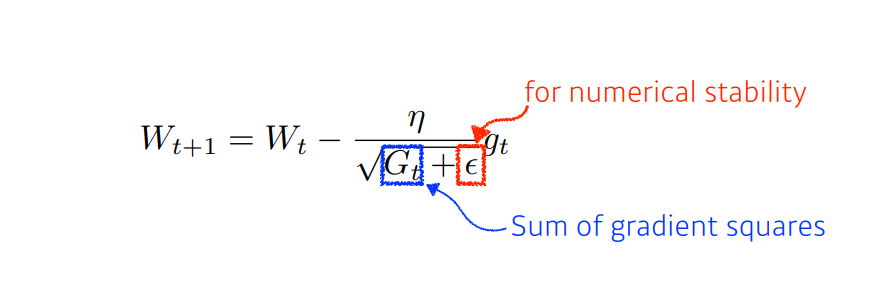
Adagrad 방식의 아이디어는 "지금 까지 많이 변화한 파라미터들은 step size(learning rate)를 작게하고, 많이 변화하지 않은 경우 step size를 크게한다" 이다. 위의 수식을 살펴보면, 기존의 step size 를 의 값에 반비례 하도록한다. ( 에서의 제곱연산은 element-wise 제곱연산이며, 업데이트 연산도 element-wise product 이다.) ( 은 zero division 을 막기 위한 numerical stability 로 과 같은 아주 작은 수)
즉, 많이 변화한 파라미터 일수록 적게 이동하고, 적게 변화한 파라미터 일수록 많이 이동하는 것이다. 그래서 학습을 진행하는 동안 보통 step size=0.01 정도를 사용한 뒤 step size decay 등을 신경 써주지 않아도 된다.
하지만 학습이 긴 시간 진행될 경우 는 계속 증가하므로 이 작아지는 문제가 발생하여 결국 거의 움직이지 않게 되는 문제가 있다.
✏️ Adadelta(Adaptive Delta)

기존의 Adagrad를 보완하기 위한 방식으로, ADADELTA : An Adaptive Learning Rage Method,2012 에 따르면 두가지 목적을 가진다.
-
학습이 길어짐에 따라 learning rate decay 문제를 해결한다.
-
직접 global learning rate를 결정해야하는 문제 를 해결한다.
기존의 Adagrad의 경우 와 같이 단순 accumulation 으로 학습이 길어짐에 따라 learning rate decay 문제가 발생한다. 또한 그 전 정보들을 다 가지고 있어야 했기 때문에 메모리 문제도 있다. 그래서 (EMA, Exponential Moving Average) 를 통해 최신의 gradient를 반영하도록 하여 해결함과 동시에 메모리 문제를 해결한다.
위의 식과 같이 최근의 gradient를 더 반영하면서도 과거의 정보 또한 exponential 하게 감소하면서 점차 사라지게 하여 한번에 버리지 않는다는 것이다.
또 다른 문제는 기존의 SGD,Momentum,Adagrad 방식의 경우 (=)와 (=)의 unit이 일치하지 않는 문제를 가지고 있었다.
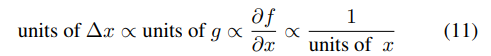
그래서 Hessian matrix 를 이용한 approximation 을 통해 unit을 수정한다.
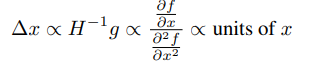
그 후 에 대한 EMA ()를 분모에 넣어줌으로써 해결하는데, 의 경우 현재 산출해야하는 값이기 때문에 t-1 까지의 RMS () 로 대체한다.
<참고>
Hessian matrix의 경우 second derivative를 표현하는 행렬 로, 함수의 곡률(Curvature) 특성 을 나타내기 때문에, Hessian 을 이용하면 second-order Talyer expansion이 가능하다고 한다. 이것이 주는 장점은 critical point의 종류를 판별할수 있다는 것인데, gradient는 first-derivative 가 0이 되는 critical point(엄밀히 stationary point)를 찾을뿐, 이 점이 extream points(극대,극소) 인지 saddle point(안장점) 인지 모르지만 Hessian 을 이용하면 찾을 수 있다.
✏️ RMSprop
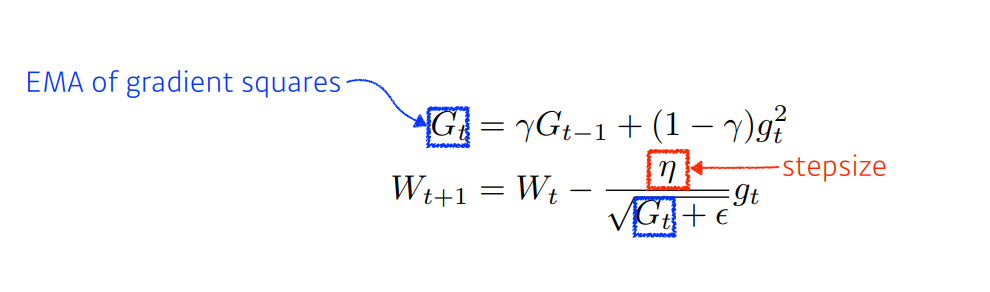
기존의 Adagrad를 보완하기 위한 방식으로, Adadelta에서 살펴봤듯이, Exponential Moving Average(EMA) 를 통해 최신의 gradient를 반영하도록 하여 해결한다.
✏️ Adam

Momentum + Adaptive 방식으로 적절한 step size 와 step 방향 을 결정하다. 보통 로는 0.9, , 정도의 값을 사용한다고 한다.
✏️ Summary
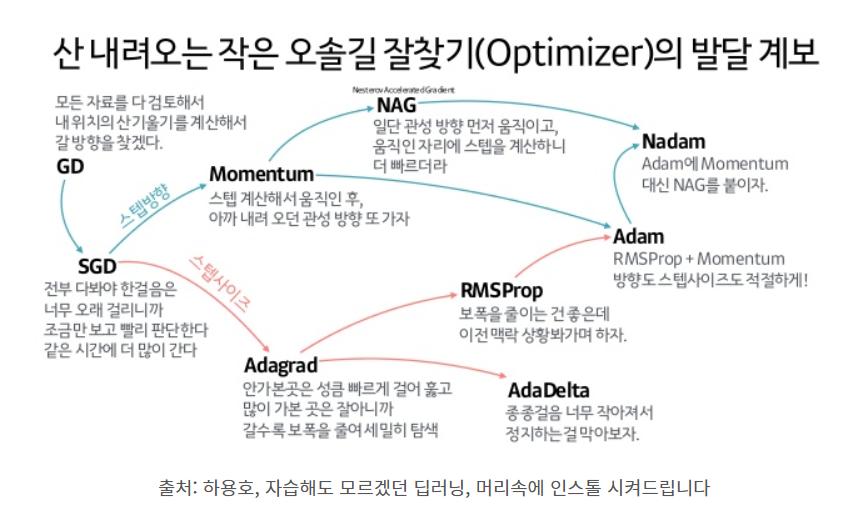
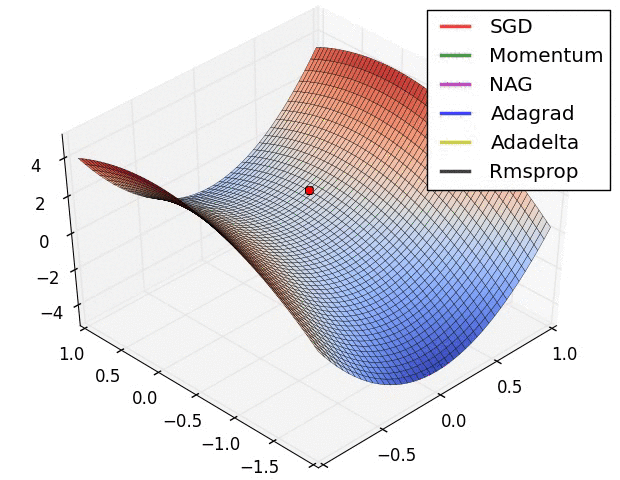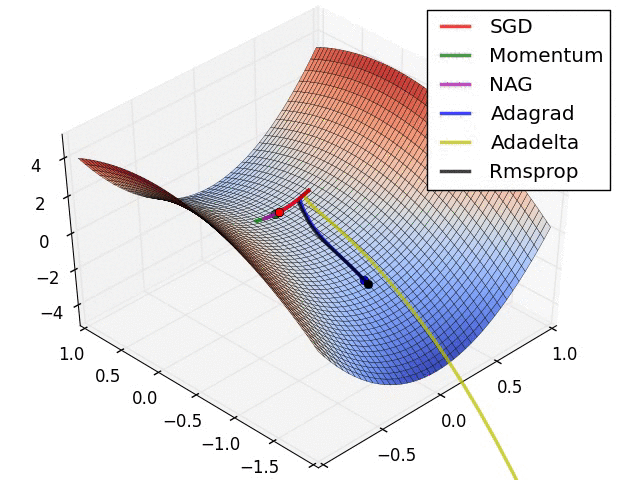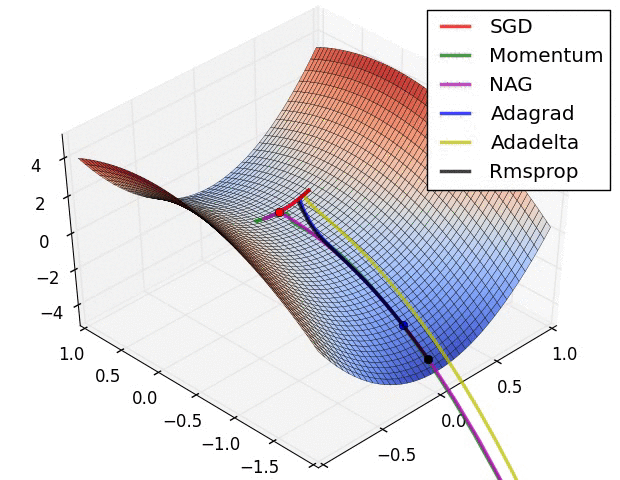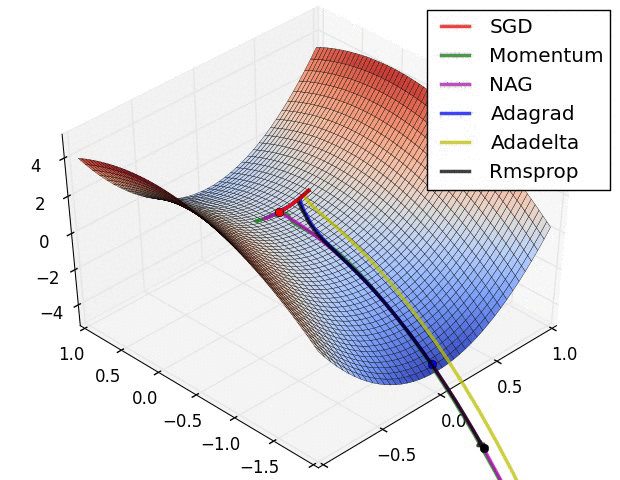
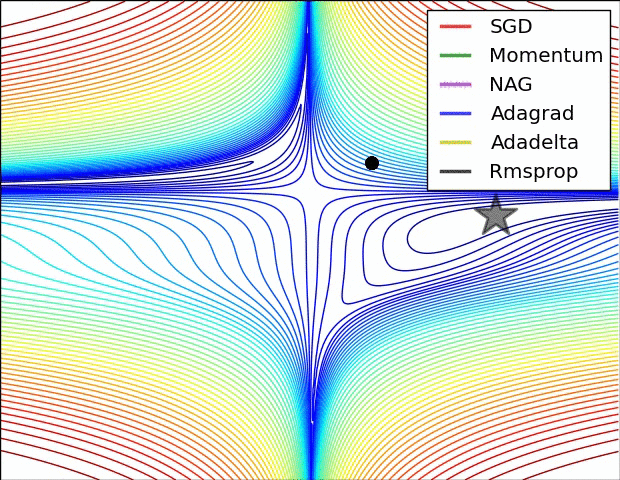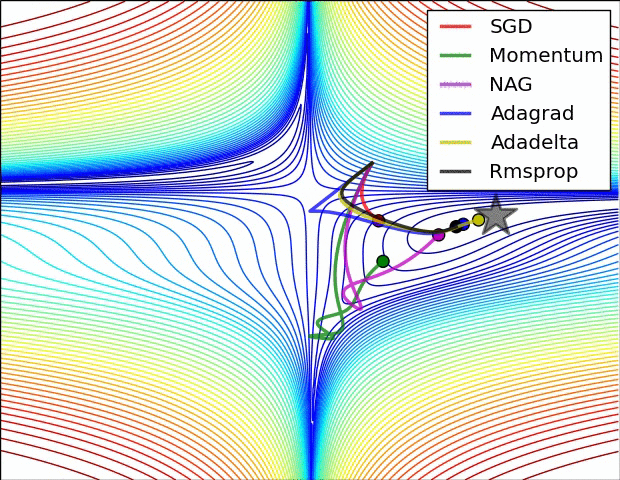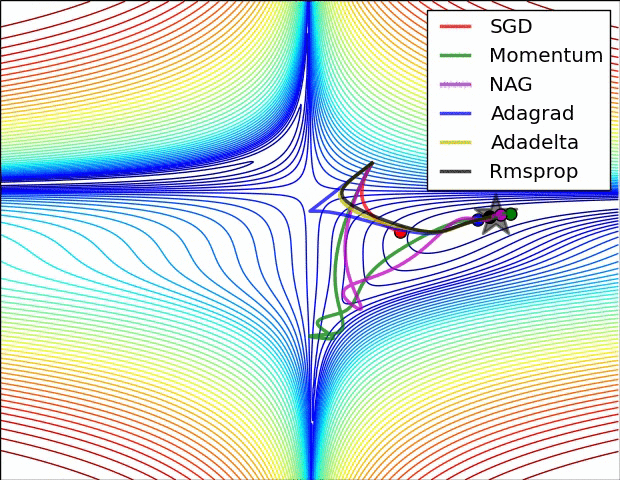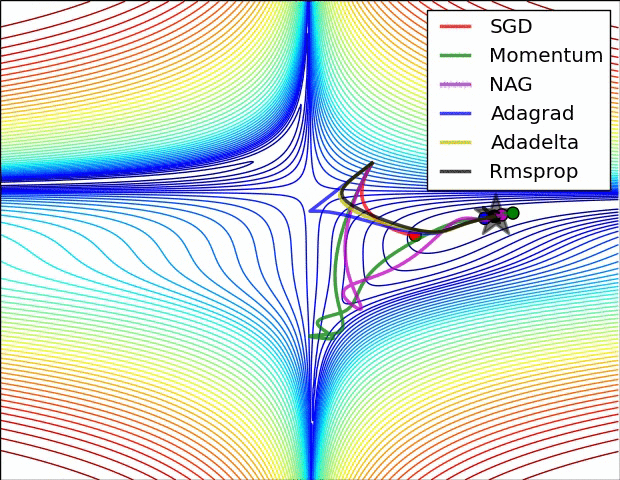
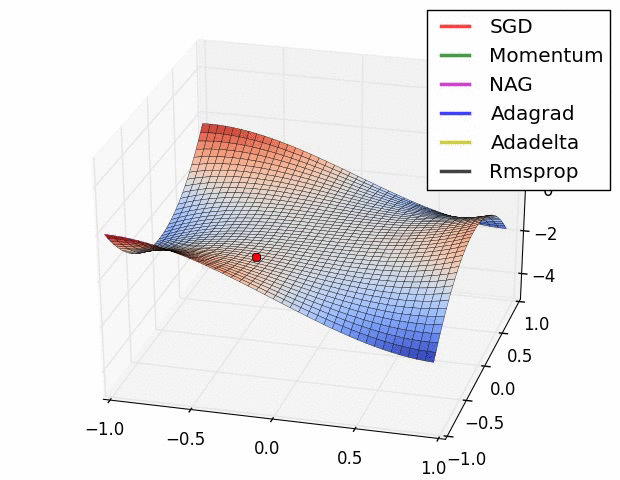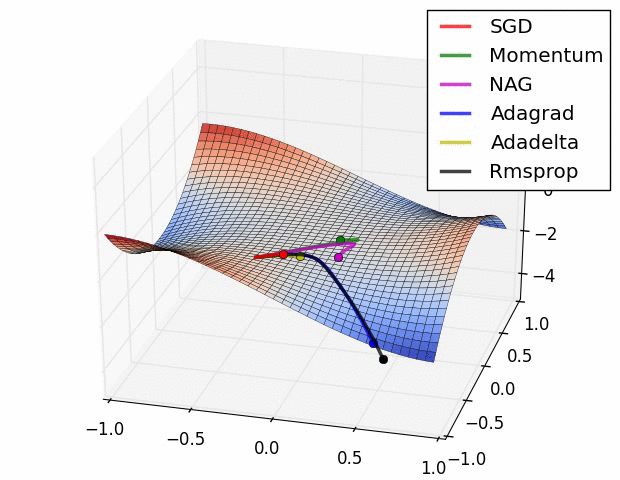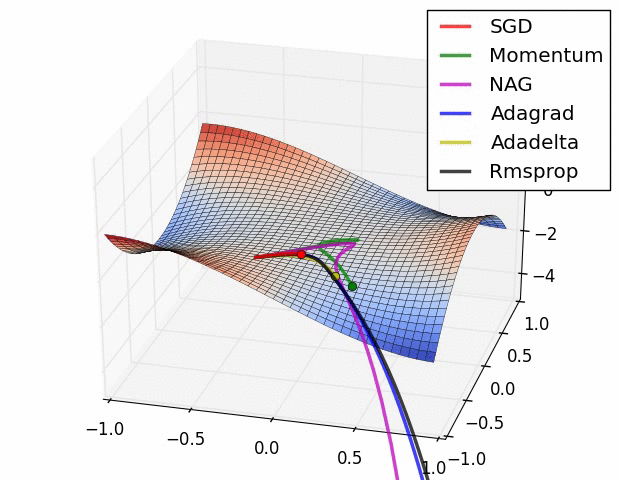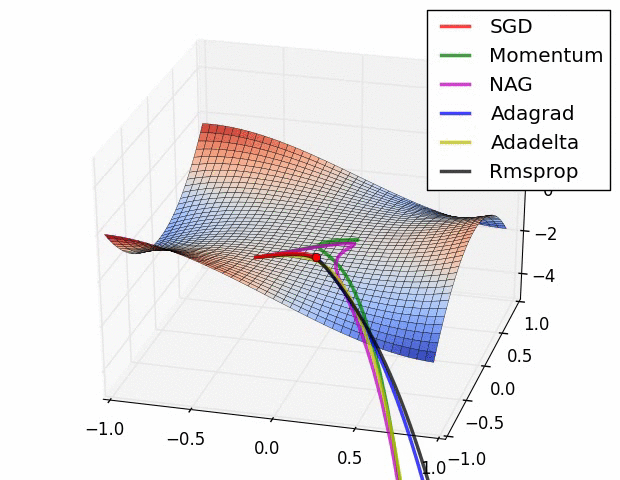
✏️ Experiment
📄 Regularization
Over-fitting을 막기 위한 regularization 에 대해 살펴보도록 한다.
✏️ Early Stopping
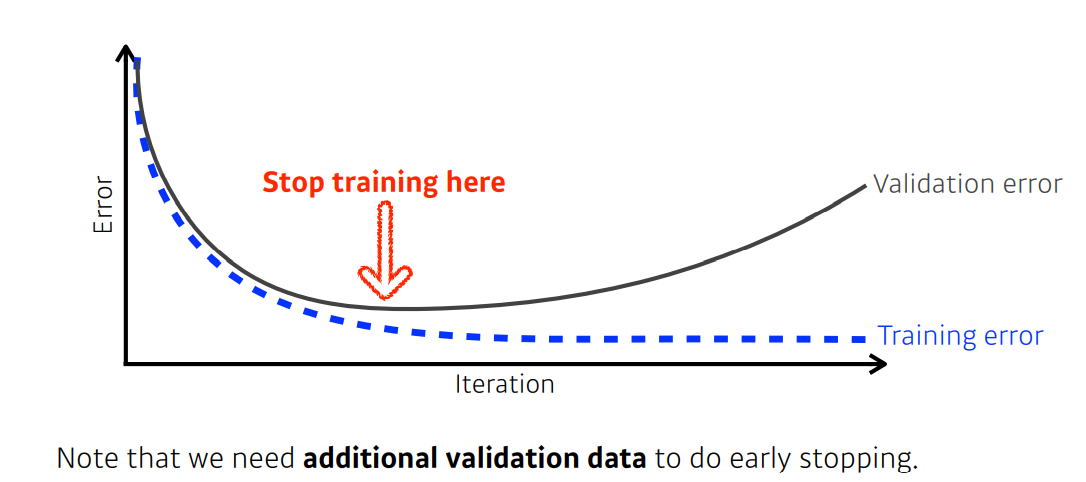
학습이 진행됨에 따라 학습데이터에 관한 오차는 작아지겠지만, 오히려 over-fitting 이 되어 generalization performance가 떨어지는 문제가 발생한다. 따라서 Early Stopping 이란 validation error가 커지기 시작하는 시점에 학습을 중단하는 기법 이다. 주의할것은 loss 값이 상하로 움직이는 경우가 생기기 때문에 직전 학습의 loss 만을 비교해서 종료하는것은 안된다. 따라서 일정 epoch 동안 계속해서 loss 가 증가하면 학습을 중단해야한다.
import numpy as np
import torch
class EarlyStopping:
def __init__(self,patience=0,verbose=True,path='check_point.pt'):
"""[summary]
Args:
patience (int): 몇 epoch 만큼 계속해서 오차가 증가하면 학습을 중단할지 결정한다.
verbose (bool): validation loss log 를 보여줄지 결정한다.
path (str, optional): model.pt 를 어디에 저장할지 결정한다.
"""
self.patience=patience
self.verbose=verbose
self.path=path
self._step=0
self._min_val_loss=np.inf
self._early_stopping=False
def __call__(self,val_loss,model):
if self._early_stopping: return
if self._min_val_loss < val_loss: #val_loss 증가
if self._step >=self.patience:
self._early_stopping=True
if self.verbose:
print(f'Validation loss increased for {self.patience} epochs...\t Best_val_loss : {self._min_val_loss}')
elif self._step<self.patience:
self._step+=1
else:
self._step=0
if self.verbose:
print(f'Validation loss decreased ({self._min_val_loss:.6f} ---> {val_loss:.6f})\tSaving model..."{self.path}"')
self._min_val_loss=val_loss
self.save_checkpoint(model)
def save_checkpoint(self,model):
torch.save(model.state_dict(),self.path)
@property
def early_stopping(self):
return self._early_stopping
✏️ Parameter Norm Penalty(Weight Decay)
학습을 진행하게 되면 일반적으로 cost function 이 작아지는 쪽으로 학습을 하게 되는데, 단순히 작아지는 쪽으로만 학습을 진행하다 보면 특정 파라미터들이 커지면서 오히려 generalization performance가 떨어지게 하는 경우도 있다. 그래서 parameter norm penalty(Weight Decay) 을 이용하여 파라미터 값들 역시 최소가 되는 방향 으로 진행하게 한다. 다음은 크게 2가지의 weight decay 방식에 대해 살펴본다.
-
L2-norm penalty
L2-norm 규제항이 더 해진 cost function 을 편미분한 식을 보면 cost function 뿐만 아니라 값들 역시 작아지는 방향으로 진행을 하게됨을 알 수 있다. 즉, 가 작아지는 방향으로 진행을 한다는 것은 weight decay 를 통해
outlier의 영향을 적게 받도록 만들어 generalization performance를 높이는 것이다. 이렇게 L2-norm penalty 를 준 모델을 Ridge model 이라 부른다. -
L1-norm penalty
L2-norm 규제항이 더 해진 cost function 을 편미분한 식을 보면 값 자체를 줄이는 것이 아닌 부호에 따른 상수값을 빼주는 방향으로 진행을 하게 됨을 알 수 있다. 즉, 상수값을 빼주어 작은 들은 거의 0으로 수렴하게 되어 특정 중요한 들만 남게 된다. 이렇게 L1-norm penalty 를 준 모델을 Lasso model 이라 부른다.
✏️ Data Augmentation
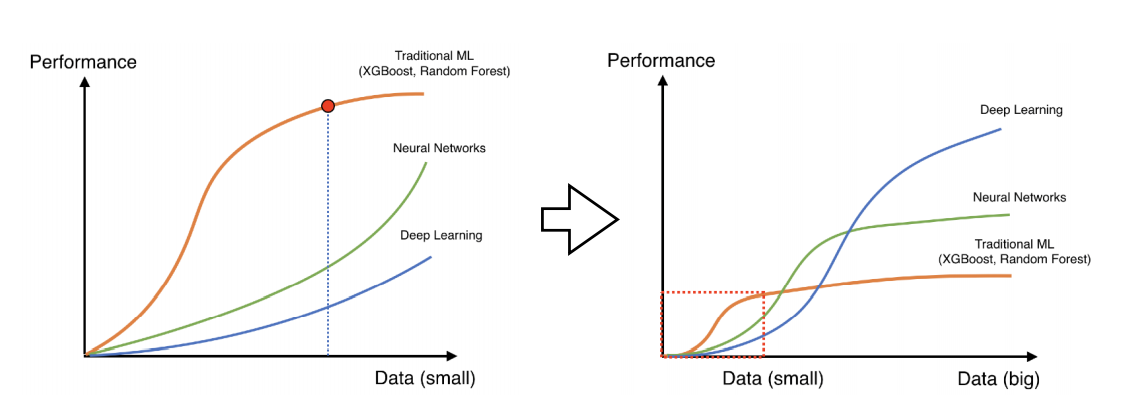
학습에 있어서 데이터는 어떤 것들보다도 중요하다. 데이터의 양이 적은 경우 기존의 ML ,NN이 좋은 성과를 나타내지만 데이터가 많아지는 경우 풍부한 표현이 가능한 DL이 압도적으로 좋은 성과를 낼 수 있다. 그래서 class 에 영향을 끼치지 않는 선에서 Data Augmentation은 필수적이다.
✏️ Noise Robustness

입력데이터 또는 가중치에 noise를 추가 하면 테스트에서 좀 더 좋은 성능을 낼 수 있다는 결과가 있다.
✏️ Label Smoothing
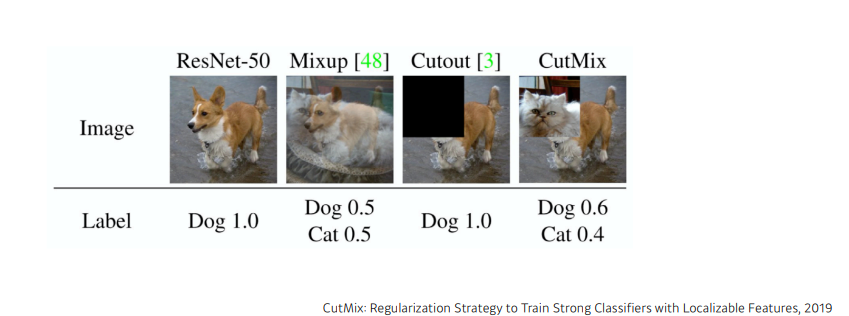
Rethinking the Inception Architecture for Computer Vision,2016 에서 제안된 기법으로 이름에서 알 수 있듯이, Hard target(label) 을 sotf target(label) 로 바꾸는 것으로 label smoothing을 통해 mislabeling 데이터를 다룸과 동시에 generalization performance를 올리는 방법이다. 예를들어, 이진 분류의 문제의 경우 label 은 0 또는 1로 주어질 것이다. 다르게 생각해보면 이것은 label 이 0 또는 1 임을 100% 확신 한다는것이다. 하지만 잘못된 annotation 으로 인해 반드시 그렇지 않을 수있다는 것이 label smoothing 에 시작점이다. 이때 발생할수 있는 잘못된 학습을 막기 위해 label을 0 또는 1이 아닌 smooth 하게 부여하는것이 label smoothing의 핵심 아이디어이다.
✏️ Dropout
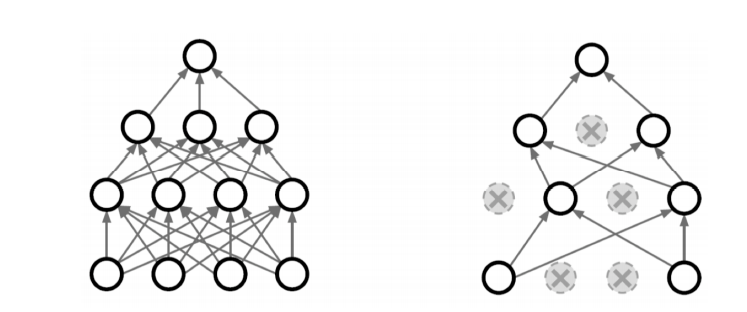
말그대로 무작위로 일부 노드들을 생략하여 학습을 진행 한다. dropout 을 통해 over-fitting을 막음 과 동시에 매번 다른 형태의 노드로 학습하기 때문에 여러 형태의 네트워크를 생성하는 앙상블 효과를 낼 수 도 있다.
✏️ Batch Normalization

Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift,2015 에 따르면 gradient vanishing/exploding 이 일어나지 않도록 하고 싶었고, 그 이유가 Internal Covariance Shift 현상(네트워크의 각 층이나 Activation마다 input 의 distribution이 달라지는 현상)이라고 말하고 있다. 그래서 mini-batch 단위의 normalization을 진행하여 다음과 같은 효과를 얻을 수 있다고 한다.
-
Learning rate 을 너무 높게 잡은 경우 gradient vanishing/exploding 가 발생하는 문제가 있는데, Batch Normalization을 통해 parameter scale에 영향을 제거하여 learning rate를 크게 잡을수 있게 되고 빠른 학습을 가능케 하는 효과가 있다.
-
regularization 효과를 가지고 있으며, Dropout와 같은 효과를 가져(Dropout의 경우 효과는 좋지만 학습속도가 다소 느려진다는 단점이 있다) Dropout을 제거함으로써 학습속도 향상 효과가 있다.
📌 CNN(Convolutional Neural Network)
📄 Convolution 연산은 왜 등장했을까?
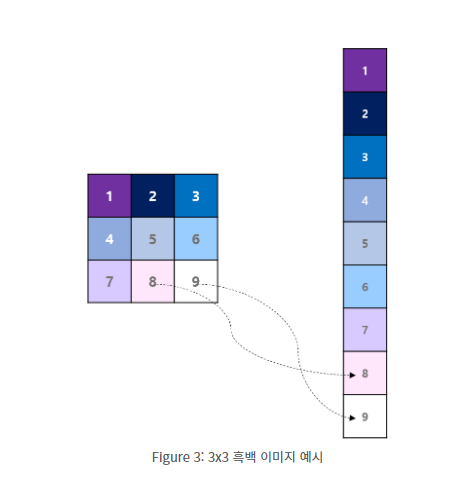
기존의 neural net에선 이미지 데이터를 flattening 하여 각 픽셀에 가중치를 곱하여 연산결과를 전달하는것과 같다. 이것은 결국 이미지가 가지는 공간적 특성을 무시한다 는 것을 쉽게 알 수 있다. 그래서 이미지의 공간적 특성을 유지 하는 것이 convolutional layer 등장의 motivation 이 되었다.
📄 Convolution 은 무엇일까?
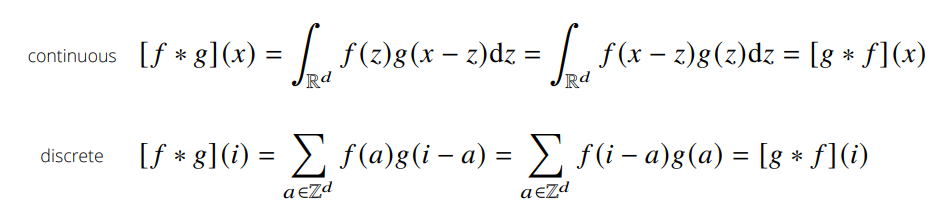
convolution은 신호(signal)을 커널을 이용해 국소적으로 증폭 또는 감소 시켜서 정보를 추출 또는 필터링하는 것이다. 다음은 convolution의 예시이다.
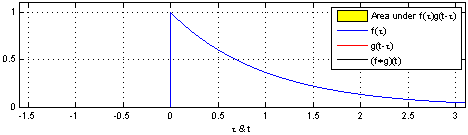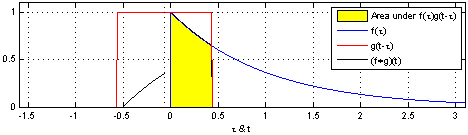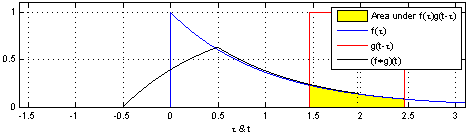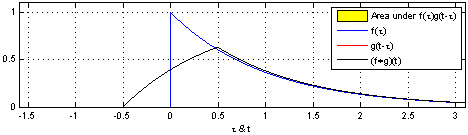
covolution과 비슷하게 Cross-correlation 연산이 있는데 convolution 연산과의 차이점은 함수를 반전시키냐 안시키냐의 차이이다.
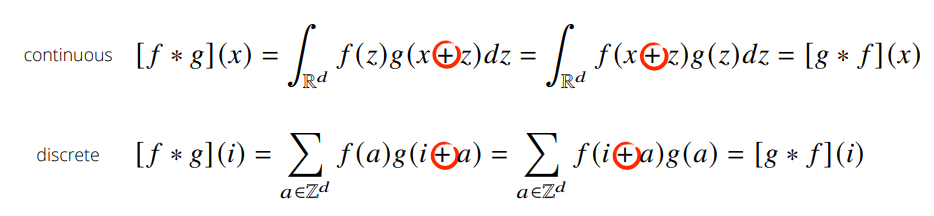
convolutional layer의 입력값에 커널을 convolution 할려면 커널을 반전시켜 적용해야 하나, 커널의 가중치 값을 학습하려는 것이 목적이기 때문에 반전하지 않아도 상관이 없다. 따라서 CNN에서 쓰이는 연산은 엄밀히는 Cross-correlation 이나 convolution 연산으로 불린다.
📄 Convolutional layer는 무엇일까?
다층 퍼셉트론에서 이미지를 처리한다고 생각한다면 다음과 같이 flattening 하여 각 가중치 연산 후 활성화 함수를 통과 시켰다.
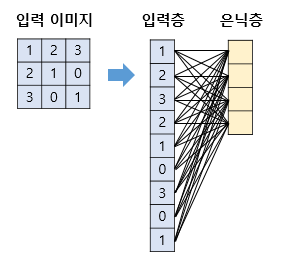
하지만 convolutional layer 에서는 모든 입력벡터에 적용되는 동일한 kernel 을 움직여가면서 생성된 결과를 활성화 함수를 통과시키게 된다.
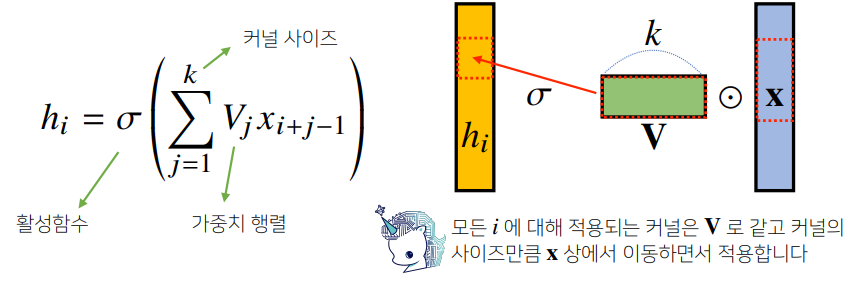
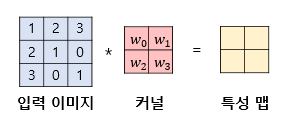
이해를 돕기 위해 kernel의 연산과정을 1차원,2차원으로 살펴보면 다음과 같다.
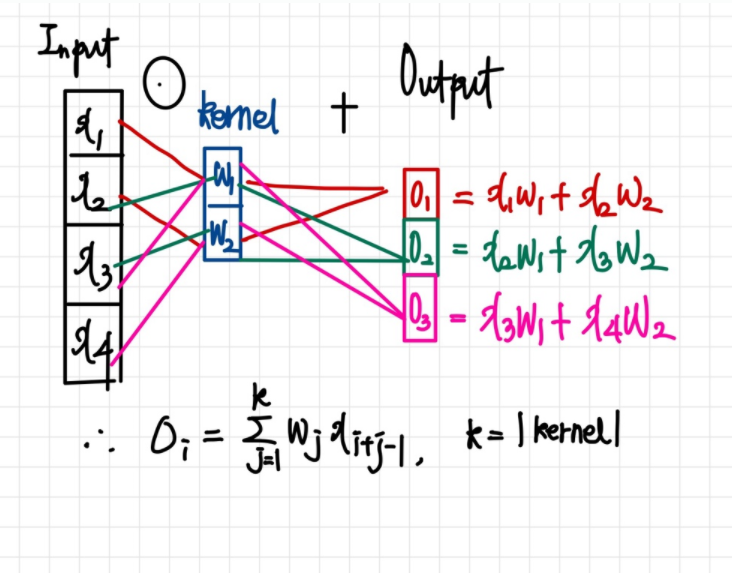
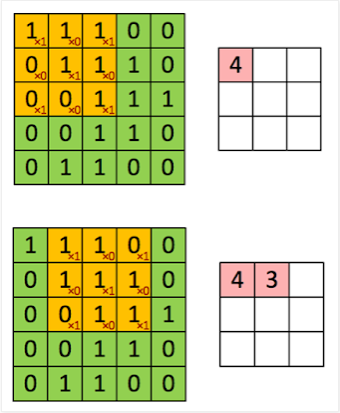
<참고>
2차원 커널연산의 예시를 확인하고 싶다면 여기를 참고하자.
📄 Convolutional layer가 주는 이점은 무엇일까?
예를들어, 다층퍼셉트론이 3x3 이미지를 처리하여 4개의 뉴론을 가지는 은닉층을 가지고 있다면 다음과 같이 총 9x4=36 개의 가충치를 가지게 된다.

그러나 합성곱 연산을 통해 처리하게 되면 일부데이터의 가중치만 사용하게 되는데, 이를 local connectivity 라 부른다.
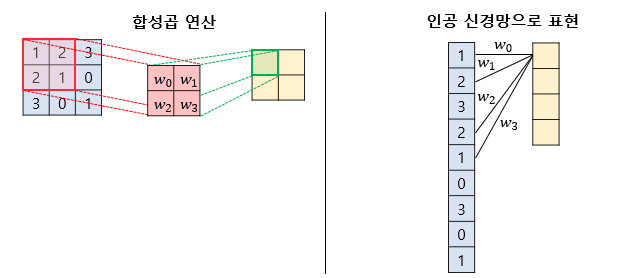
즉, fully connected layer 와 비교하면 일부만 연결하고 같은 가중치(sharing weight)를 여러번 사용하여 계산량을 줄일 수 있음과 동시에 공간적 구조 정보를 보존할 수 있는 이점이 있다.
📄 Convolutional layer의 역전파 어떻게 동작할까?
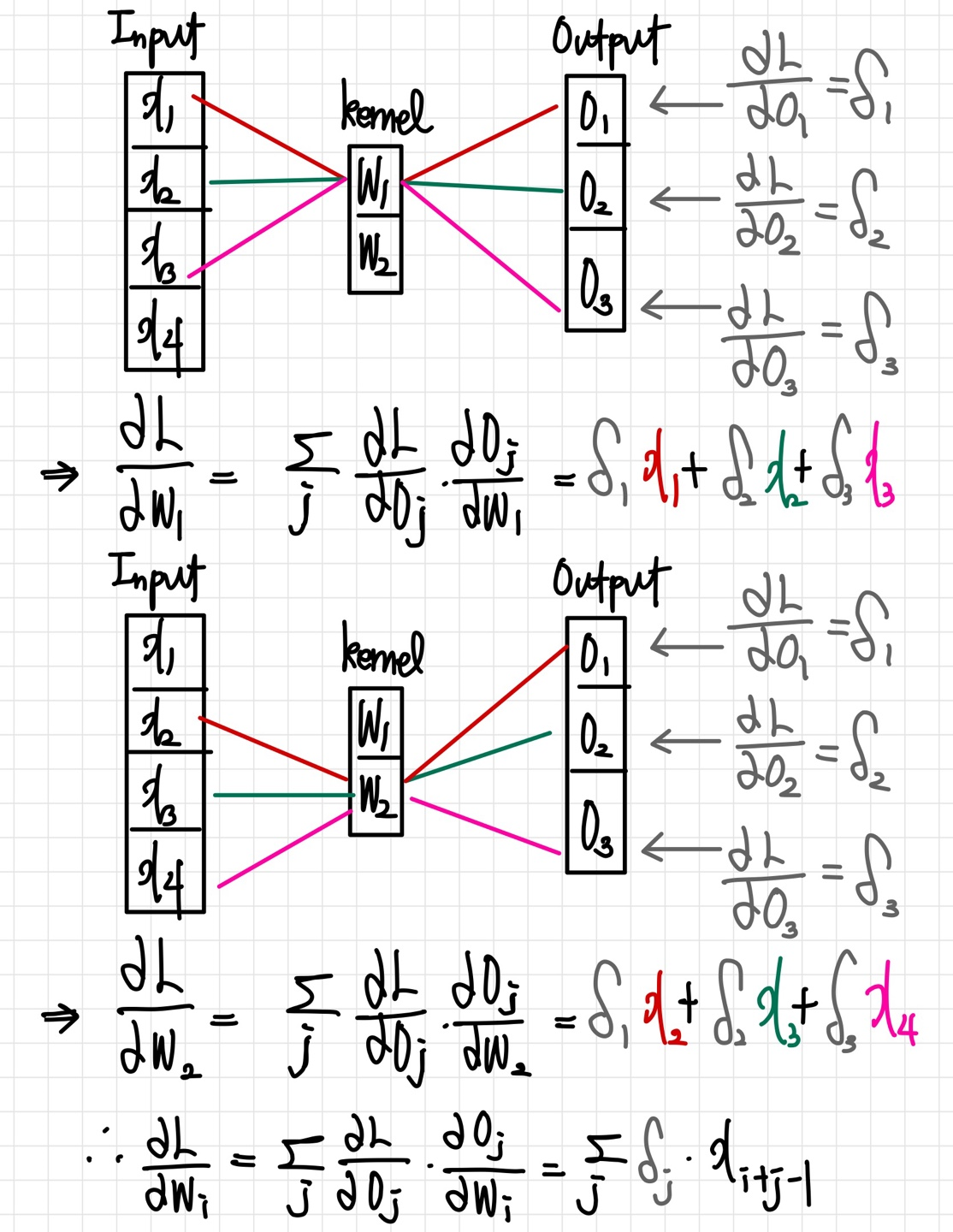
위의 수식을 살펴보면, convolution 연산은 커널이 모든 입력데이터에 공통으로 적용되기 때문에 역전파 계산 역시 convolution 연산임을 확인할 수 있다.
📚 Reference
Under-fitting vs Over-fitting1
Under-fitting vs Over-fitting2
Bias and Variance Tradeoff
Cross-validation1
Cross-validation2
Cross-validation3
Bagging vs Boosting
Batch-size
Gradient Descent Optimization Algorithms
Momentum, Nestrov Accelerated Gradient
Adadelta
Parameter Norm Penalty(Weight Decay)
Batch Normalization
Convolution vs Cross-correlation
Convolutional Neural Network1
Convolutional Neural Network2
