[부스트캠프 AI Tech] U-stage. 2-1

느린 개발자·2021년 1월 25일
부스트캠프
1

부스트캠프 AI Tech

목록 보기
7/35
post-custom-banner

📌 Numpy

파이썬의 고성능 과학 계산용 패키지로, Matrix 와 Vector 와 같은 Array 연산의 표준 으로 불리운다.
넘파이(Numpy) 는 일반 List에 비해 빠르고, 메모리 효율적이다. 또한 반복문 없이 데이터 배열에 대한 처리를 치원하고 선형대수와 관련된 다양한 기능을 제공한다.

📄 Array creation

Numpy의 array는 python list와는 다르게 순차적인 데이터 저장 구조 방식으로 저장용량 과 접근 방식의 비용에 있어서 더 효율적이다. 또한 하나의 데이터 type 만 배열에 넣을수 있다. 즉, dynamic typing 을 지원하지 않는다.

import numpy as np
data=np.array([1,2,3,'4'],dtype=np.float32)
data

#array([1., 2., 3., 4.], dtype=float32)
data_1D=np.array([1,2,3,4],dtype=np.int32)
data_1D.shape # Vector ,(4,)
#####################################

data_2D=np.array([[1,2,3],
                  [4,5,6]],dtype=np.int32)
data_2D.shape # Matrix ,(2,3)
#####################################

data_3D=np.array([[[1,2,3],[4,5,6]],
                  [[1,2,3],[4,5,6]],
                  [[1,2,3],[4,5,6]]],dtype=np.int32)
data_3D.shape # 3-tensor ,(3,2,3)

📄 Array dtype

ndarray의 single element 가 가지는 data type 으로 각 element가 차지하는 memory 의 크기가 결정된다.

np.array([[1,2,3],[4.5,'6','5']],dtype=np.float32).nbytes # 32bit = 1byte *4 =4bytes -> 6 *4bytes =24bytes
# 24

📄 Handling shape

✏️ Reshape

Array의 크기를 element의 갯수는 유지하면서 변형한다.

test_matrix=np.arange(10).reshape(2,5) # vector -> 2x5 matrix 
test_matrix 
# array([[0, 1, 2, 3, 4],
# 	[5, 6, 7, 8, 9]])

✏️ Flatten

다차원 array를 1차원 array로 변환한다.

test_matrix=np.arange(10).reshape(2,5) # 2x5 matrix
test_matrix.flatten()
# array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

📄 Indexing & Slicing

✏️ Indexing

list 와 달리 [index_1,index_2,...] 인덱싱 을 제공한다

test_matrix=np.arange(6).reshape(3,2)
test_matrix
#     array([[0, 1],
#           [2, 3],
#           [4, 5]])

test_matrix[2,1] # ==test_matrix[2][1]

#5

✏️ Slicing

list 와 달리 행과 열부분을 나눠서 slicing이 가능 하여 matrix의 부분집합을 추출할때 유용하다.

test_matrix=np.arange(15).reshape(3,5)
test_matrix
#    array([[ 0,  1,  2,  3,  4],
#           [ 5,  6,  7,  8,  9],
#           [10, 11, 12, 13, 14]])

test_matrix[:,1] # row 전체, 두번째열
#    array([ 1,  6, 11])

test_matrix[:,:] # == test_matrix == test_matrix[:]
#    array([[ 0,  1,  2,  3,  4],
#           [ 5,  6,  7,  8,  9],
#           [10, 11, 12, 13, 14]])

test_matrix[::2,::3]
#    array([[ 0,  3],
#           [10, 13]])

📄 Creation function

✏️ arange

list의 range 처럼 array의 범위를 지정하여 생성한다. list의 range 와의 차이점은 step의 경우 floating point도 표시가능하다.

np.arange(30,50,0.5) # floating point 도 가능하다

#    array([30. , 30.5, 31. , 31.5, 32. , 32.5, 33. , 33.5, 34. , 34.5, 35. ,
#           35.5, 36. , 36.5, 37. , 37.5, 38. , 38.5, 39. , 39.5, 40. , 40.5,
#           41. , 41.5, 42. , 42.5, 43. , 43.5, 44. , 44.5, 45. , 45.5, 46. ,
#           46.5, 47. , 47.5, 48. , 48.5, 49. , 49.5])

✏️ Ones / Zeros / Empty / Something_like

  • ones : 1로 가득찬 ndarray 생성
  • zeros : 0으로 가득찬 ndarray 생성
  • empty : shape만 주어지고 비어있는 ndarray 생성(memory initialization이 되지 않음)
  • somthing_like - 기존 ndarray의 shape 크기 만큼 1, 0, 또는 empty array 생성
np.zeros((2,5)) # 2x5 - zero matrix
#  array([[0., 0., 0., 0., 0.],
#           [0., 0., 0., 0., 0.]])

np.ones((2,5)) # 2x5 - one matrix

#    array([[1., 1., 1., 1., 1.],
#           [1., 1., 1., 1., 1.]])

np.empty((2,5)) # 2x5 - empty matrix (결과는 one matrix 가 생성된것같지만 해당 메모리의 값이 1로 쓰레기값이 남아 있어서이다)
 
#    array([[1., 1., 1., 1., 1.],
#           [1., 1., 1., 1., 1.]])


test_matrix=np.arange(30).reshape(5,6)
np.ones_like(test_matrix) # 5x6 one matrix
# array([[1, 1, 1, 1, 1, 1],
#           [1, 1, 1, 1, 1, 1],
#           [1, 1, 1, 1, 1, 1],
#           [1, 1, 1, 1, 1, 1],
#           [1, 1, 1, 1, 1, 1]])

✏️ Identity

단위행렬을 생성한다

np.identity(n=3,dtype=np.float32)
# array([[1., 0., 0.],
#           [0., 1., 0.],
#           [0., 0., 1.]], dtype=float32)

✏️ Eye

대각선이 1인 행렬로 identity와의 차이점은 shape 설정과 k값을 통해 start index 설정이 가능하다

np.eye(3)
#  array([[1., 0., 0.],
#           [0., 1., 0.],
#           [0., 0., 1.]])

np.eye(3,5,k=2)
#    array([[0., 0., 1., 0., 0.],
#           [0., 0., 0., 1., 0.],
#           [0., 0., 0., 0., 1.]])

✏️ Diag

대각행렬의 값을 추출하며 이 또한 k값을 통해 start index 설정이 가능하다

matrix=np.arange(9).reshape(3,3)
matrix
#    array([[0, 1, 2],
#           [3, 4, 5],
#           [6, 7, 8]])

np.diag(matrix)
#    array([0, 4, 8])

np.diag(matrix,k=1) 
#    array([1, 5])

✏️ Random sampling

데이터 분포에 따른 sampling으로 array를 생성한다

np.random.uniform(0,1,10).reshape(2,5) # 균등분포
#  array([[0.08602674, 0.74042107, 0.15989891, 0.65901218, 0.71817766],
#           [0.34351467, 0.32649185, 0.18205676, 0.14635388, 0.68248751]])
np.random.normal(0,1,10).reshape(2,5) # 정규분포
#    array([[ 0.12853111,  0.39784715,  1.34587716, -0.20692527,  0.53340462],
#           [ 1.19029392, -0.72233091,  0.79634839,  0.67064794,  0.13323741]])

📄 Operation function

✏️ Axis

Operation function 및 Comparison 을 실행할때 기준이 되는 dimension 축으로 이 부분을 잘 이해하고 있어야 한다

✏️ Sum / Mean / Std / Mathematical functions

  • sum: ndarray의 element 들 간의 합.
  • mean: ndarray의 element 들 간의 평균.
  • std : ndarray의 element 들 간의 표준편차.
  • mathematical functions : 다양한 수학연산자를 제공하므로 필요한 내용은 레퍼런스 참조.

test_matrix=np.arange(10).reshape(2,5)
test_matrix
#    array([[0, 1, 2, 3, 4],
#           [5, 6, 7, 8, 9]])

test_matrix.sum()
#    45

test_matrix.sum(axis=1)  #axis=1을 기준으로 summation
#    array([10, 35])


test_matrix.mean()
# 4.5

test_matrix.std()
#    2.8722813232690143

✏️ Concatenate

numpy array를 붙이는 함수를 제공한다.

  • vstack : vertical 방향으로 붙인다
  • hstack : horizontal 방향으로 붙인다
  • concatenate : 두 array를 axis 기준으로 붙인다
a=np.array([1,2,3])
b=np.array([4,5,6])

np.vstack((a,b))
#    array([[1, 2, 3],
#           [4, 5, 6]])

np.hstack((a,b))
#    array([1, 2, 3, 4, 5, 6])

np.concatenate((a,b),axis=0) # == np.hstack((a,b))
#    array([1, 2, 3, 4, 5, 6])

📄 Array Operation

numpy는 array간의 기본적인 사칙연산을 지원한다. 주의할것은 기본적인 연산 의 경우 element-wise operation 이며, 행렬 곱연산을 원할경우 dot함수를 이용하자.

✏️ Basic element-wise operations

test_a=np.array([[1,2,3],
                 [4,5,6]])
test_a+test_a
#    array([[ 2,  4,  6],
#           [ 8, 10, 12]])

test_a-test_a
#    array([[0, 0, 0],
#           [0, 0, 0]])

test_a*test_a
#    array([[ 1,  4,  9],
#           [16, 25, 36]])

test_a/test_a
# array([[1., 1., 1.],
#           [1., 1., 1.]])

test_a//test_a
#   array([[1, 1, 1],
#           [1, 1, 1]], dtype=int32)

test_a%test_a
#    array([[0, 0, 0],
#           [0, 0, 0]], dtype=int32)

✏️ Dot

matrix의 기본연산은 dot함수를 사용한다.

test_a=np.array([[1,2,3],
                 [4,5,6]]) #2x3
test_b=test_a.T # ==test_a.transpose()

test_a.dot(test_b) # 2x2

#    array([[14, 32],
#           [32, 77]])

✏️ Broadcasting

shape이 다른 배열간 연산을 지원해준다.

test_scalar=3
test_vector=np.arange(2) # [0,1]
test_matrix=np.arange(4).reshape(2,2) # [[0,1],[2,3]]

test_vector-test_scalar # Vector - scalar
#    array([-3, -2])

test_matrix-test_scalar # Matrix - scalar
#    array([[-3, -2],
#           [-1,  0]])

test_matrix-test_vector # Matrix - vector
#    array([[0, 0],
#           [2, 2]])

📄 Comparison

✏️ All/Any

데이터의 전부(and) 또는 일부(or) 가 조건 만족여부 반환한다.

a=np.arange(10) # [0,1,2,3,4,5,6,7,8,9]
np.all(a>5) # False
np.any(a>8) # True

✏️ Comparison operation

numpy는 배열의 크기가 동일할때 element 간 비교의 결과를 boolean type의 array로 반환해준다.

test_a=np.array([1,3,0])
test_b=np.array([5,2,1])

test_a>test_b
# array([False,  True, False])

test_a==test_b
#    array([False, False, False])

(test_a>test_b).any()
# True
np.logical_and(test_a>1,test_b<3)
#  array([False,  True, False])

np.logical_not(test_a>1) # test_a<=1
#    array([ True, False,  True])


np.logical_or(test_a>1,test_b<3) 
#    array([False,  True,  True])

✏️ Where

조건을 만족하는 index를 반환해준다.

test_a=np.array([1,3,0])
np.where(test_a>1,2,-2) # where(condition,True일경우 값 변환,False일경우 값변환)
# array([-2,  2, -2])

np.where(test_a>1) # Index 반환
#    (array([1], dtype=int64),)


test_b=np.array([1,np.NaN,np.Inf])
np.isnan(test_b)
#    array([False,  True, False])

np.isfinite(test_b)
#    array([ True, False, False])

✏️ Argmax / Argmin

arry 내 최대값 또는 최소값의 index를 반환해준다

test_a=np.arange(10).reshape(2,5)
test_a
#    array([[0, 1, 2, 3, 4],
#           [5, 6, 7, 8, 9]])
np.argmax(test_a,axis=1)
#    array([4, 4], dtype=int64)

np.argmin(test_a[1]) #test_a[1] = [5,6,7,8,9]
# 0

📄 Boolean & Fancy index

✏️ Boolean index

특정조건에 따른 boolean 값을 이용하여 해당 element 추출 가능.

test_array=np.array([1,-1,2,3,-3])
test_array[test_array>0] # 양수만 추출
#    array([1, 2, 3])

✏️ Fancy index

array를 index 로 사용해서 해당 element 추출 가능.

test_array=np.array([1,-1,2,3,-3])
fancy_index=np.array([0,2,3,2],dtype=np.int8) # 0,2,3,2 번 인덱스 element 추출. 반드시 integer로 선언
test_array[fancy_index]
#    array([1, 2, 3, 2])

test_array.take(fancy_index)  # take : bracket index 와 같은 효과
#    array([1, 2, 3, 2])

test_matrix=np.array([[1,4],[9,16]])
row_fancy=np.array([0,1,1],dtype=np.int8)
column_fancy=np.array([1,1,0],dtype=np.int8)
test_matrix[row_fancy,column_fancy] # Matrix에도 가능
#    array([ 4, 16,  9])

📌 Vector

📄 벡터는 무엇인가요?

벡터는 크기 와 방향 을 가지는 n-차원 공간에서의 한점 이다. 일반적으로 벡터는 열벡터(Column vector) 로 표현된다.

x=[ x1x2..xn](Column   vector),xT=[x1x2...xn](Row   vector)\textbf{x}=\begin{bmatrix}\ x_1 \\ x_2 \\ .. \\ x_n \end{bmatrix}(Column\ \ \ vector),\\ \textbf{x}^T=\begin{bmatrix} x_1 &x_2 &... &x_n \end{bmatrix}(Row \ \ \ vector)

벡터는 크기 와 방향 을 가지고 있기 때문에 원점 기준의 상대적 위치 또는 다른 벡터로 부터의 상대적 위치 이동 을 표현할 수 있다.

📄 벡터의 기본 연산은 어떻게 하나요?

  1. 성분곱(Hadamard product)

    x=[x1x2x3...xn],y=[y!y2y3...yn],x⊙y=[x1y1x2y2x3y3...xnyn]\textbf{x}=\begin{bmatrix}x_1 \\ x_2 \\ x_3 \\ ... \\ x_n \end{bmatrix}, \textbf{y}=\begin{bmatrix}y_! \\ y_2 \\ y_3 \\ ... \\ y_n \end{bmatrix}, \textbf{x}\odot \textbf{y}=\begin{bmatrix}x_1y_1 \\ x_2y_2 \\ x_3y_3 \\ ... \\ x_ny_n \end{bmatrix}
  1. 덧셈
x=[x1x2x3...xn],y=[y!y2y3...yn],x+y=[x1+y1x2+y2x3+y3...xn+yn]\textbf{x}=\begin{bmatrix}x_1\\ x_2\\ x_3\\ ...\\ x_n\end{bmatrix},\textbf{y}=\begin{bmatrix}y_!\\ y_2\\ y_3\\ ...\\ y_n\end{bmatrix},\textbf{x} + \textbf{y}=\begin{bmatrix}x_1+y_1\\ x_2+y_2\\ x_3+y_3\\ ...\\ x_n+y_n\end{bmatrix}

  1. 뺄셈
x=[x1x2x3...xn],y=[y!y2y3...yn],x−y=[x1−y1x2−y2x3−y3...xn−yn]\textbf{x}=\begin{bmatrix}x_1\\ x_2\\ x_3\\ ...\\ x_n\end{bmatrix},\textbf{y}=\begin{bmatrix}y_!\\ y_2\\ y_3\\ ...\\ y_n\end{bmatrix},\textbf{x} - \textbf{y}=\begin{bmatrix}x_1-y_1\\ x_2-y_2\\ x_3-y_3\\ ...\\ x_n-y_n\end{bmatrix}

  1. 스칼라곱
    x=[x1x2x3...xn],ax=[ax1ax2ax3...axn]\textbf{x}=\begin{bmatrix}x_1\\ x_2\\ x_3\\ ...\\ x_n\end{bmatrix},a\textbf{x}=\begin{bmatrix}ax_1\\ ax_2\\ ax_3\\ ...\\ ax_n\end{bmatrix}

📄 노름(Norm) 은 무엇인가요?

벡터의 노름(Norm)은 원점에서부터의 거리 를 말한다. 벡터의 노름 정의방법은 여러가지가 있지만 여기에선 대표적으로 L1-norm 과 L2-norm 를 살펴본다.

  1. L1-norm
    각 성분의 변화량의 절대값 을 모두 더한다.
∥x∥1=∑i=1n∣xi∣\left \| \textbf{x} \right \|_1 = \sum^n_{i=1}\left | x_i \right |

  1. L2-norm
    유클리드 거리를 계산한다.
∥x∥2=∑i=1n∣xi∣2\left \| \textbf{x} \right \|_2 =\sqrt{ \sum^n_{i=1}\left | x_i \right |^2}

위에서 다른 노름을 살펴본 이유는 노름의 종류에 따라 기하학적 성질 이 달라지는데, 머신러닝에선 각 성질들이 필요할 때가 있으므로 둘 다 사용한다.

📄 벡터 사이의 거리는 어떻게 구하나요?

두 벡터 사이의 거리는 벡터의 뺄셈 을 이용하며 노름 정의 에 따라 달라질 수 있다.

📄 두 벡터 사이의 각도는 어떻게 구하나요?

제 2 코사인법칙 으로 두 벡터 사이의 각도를 계산할 수 있다. 주의할것은 L1-norm에서는 각도를 계산할 수 없다.

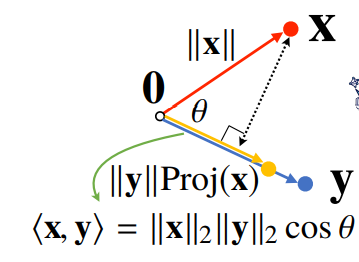
📄 내적은 무엇인가요?

크기가 같은 벡터에 대한 연산으로 연산의 결과는 스칼라 이다.

<x,y>=∑i=1dxiyi<\textbf{x},\textbf{y}>=\sum^d_{i=1}x_iy_i

📄 내적은 어떤 의미를 줄까요?

내적은 정사영(Orthogonal projection) 된 벡터의 길이와 관련 있다. 즉, Proj(x) 는 벡터 y\textbf{y} 로 정사영된 벡터 x\textbf{x}의 그림자를 의미하며 그 그림자의 길이는 ∥x∥cosΘ\left \| \textbf{x} \right \|cos\Theta 이다.

📌 Matrix

📄 행렬은 무엇인가요?

행렬은 행벡터(Row vector) 와 열벡터(Column vector) 로 이루어진 2차원 배열이다.

📄 행렬의 기본연산은 어떻게 하나요?

  1. 성분곱(Hadamard product)

    X=[x11x12...x1mx21x22...x2m............xn1xn2...xnm],Y=[y11y12...y1my21y22...y2m............yn1yn2...ynm]X⊙Y=[x11y11x12y12...x1my1mx21y21x22y22...x2my2m............xn1yn1xn2yn2...xnmynm]\textbf{X}=\begin{bmatrix} x_{11} &x_{12} & ... &x_{1m} \\ x_{21} &x_{22} & ... &x_{2m} \\ ... &... & ... &... \\ x_{n1} &x_{n2} & ... &x_{nm} \\ \end{bmatrix}, \textbf{Y}=\begin{bmatrix} y_{11} &y_{12} & ... &y_{1m} \\ y_{21} &y_{22} & ... &y_{2m} \\ ... &... & ... &... \\ y_{n1} &y_{n2} & ... &y_{nm} \\ \end{bmatrix} \textbf{X} \odot\textbf{Y}=\begin{bmatrix} x_{11}y_{11} &x_{12}y_{12} & ... &x_{1m}y_{1m} \\ x_{21}y_{21} &x_{22}y_{22} & ... &x_{2m}y_{2m} \\ ... &... & ... &... \\ x_{n1}y_{n1} &x_{n2}y_{n2} & ... &x_{nm}y_{nm} \\ \end{bmatrix}

  1. 덧셈

    X=[x11x12...x1mx21x22...x2m............xn1xn2...xnm],Y=[y11y12...y1my21y22...y2m............yn1yn2...ynm]X+Y=[x11+y11x12+y12...x1m+y1mx21+y21x22+y22...x2m+y2m............xn1+yn1xn2+yn2...xnm+ynm]\textbf{X}=\begin{bmatrix} x_{11} &x_{12} & ... &x_{1m} \\ x_{21} &x_{22} & ... &x_{2m} \\ ... &... & ... &... \\ x_{n1} &x_{n2} & ... &x_{nm} \\ \end{bmatrix}, \textbf{Y}=\begin{bmatrix} y_{11} &y_{12} & ... &y_{1m} \\ y_{21} &y_{22} & ... &y_{2m} \\ ... &... & ... &... \\ y_{n1} &y_{n2} & ... &y_{nm} \\ \end{bmatrix} \textbf{X+Y}=\begin{bmatrix} x_{11}+y_{11} &x_{12}+y_{12} & ... &x_{1m}+y_{1m} \\ x_{21}+y_{21} &x_{22}+y_{22} & ... &x_{2m}+y_{2m} \\ ... &... & ... &... \\ x_{n1}+y_{n1} &x_{n2}+y_{n2} & ... &x_{nm}+y_{nm} \\ \end{bmatrix}

  1. 뺄셈

    X=[x11x12...x1mx21x22...x2m............xn1xn2...xnm],Y=[y11y12...y1my21y22...y2m............yn1yn2...ynm]X-Y=[x11−y11x12−y12...x1m−y1mx21−y21x22−y22...x2m−y2m............xn1−yn1xn2−yn2...xnm−ynm]\textbf{X}=\begin{bmatrix} x_{11} &x_{12} & ... &x_{1m} \\ x_{21} &x_{22} & ... &x_{2m} \\ ... &... & ... &... \\ x_{n1} &x_{n2} & ... &x_{nm} \\ \end{bmatrix}, \textbf{Y}=\begin{bmatrix} y_{11} &y_{12} & ... &y_{1m} \\ y_{21} &y_{22} & ... &y_{2m} \\ ... &... & ... &... \\ y_{n1} &y_{n2} & ... &y_{nm} \\ \end{bmatrix} \textbf{X-Y}=\begin{bmatrix} x_{11}-y_{11} &x_{12}-y_{12} & ... &x_{1m}-y_{1m} \\ x_{21}-y_{21} &x_{22}-y_{22} & ... &x_{2m}-y_{2m} \\ ... &... & ... &... \\ x_{n1}-y_{n1} &x_{n2}-y_{n2} & ... &x_{nm}-y_{nm} \\ \end{bmatrix}
  1. 스칼라곱
    X=[x11x12...x1mx21x22...x2m............xn1xn2...xnm],aX=[ax11ax12...ax1max21ax22...ax2m............axn1axn2...axnm]\textbf{X}=\begin{bmatrix} x_{11} &x_{12} & ... &x_{1m} \\ x_{21} &x_{22} & ... &x_{2m} \\ ... &... & ... &... \\ x_{n1} &x_{n2} & ... &x_{nm} \\ \end{bmatrix}, a\textbf{X}=\begin{bmatrix} ax_{11} &ax_{12} & ... &ax_{1m} \\ ax_{21} &ax_{22} & ... &ax_{2m} \\ ... &... & ... &... \\ ax_{n1} &ax_{n2} & ... &ax_{nm} \\ \end{bmatrix}

  1. 곱셈

    i번째 행벡터와 j번째 열벡터 사이의 내적 을 성분으로 가지는 행렬이다.

numpy의 @ 연산을 사용하여 계산할수 있다.

x=np.array([[1,2],

​      [3,4]])



y=np.array([[-1,-2],

​      [-3,-4]])

x@y # x.dot(y)
# array([[ -7, -10],
#       [-15, -22]])

📄 행렬은 어떤 의미를 줄까요?

  1. 데이터

    벡터가 공간에서 한점을 나타냈다면, 행렬은 여러점들을 나타낸다.

    즉, 행렬의 행벡터 xi\textbf{x}_i 는 i번째 데이터 를 의미하며, 행렬의 xijx_{ij}는 i번째 데이터의 j번째 변수의 값 을 의미한다.

  2. 연산자(Operator)

    행렬의 곱은 벡터공간에서 사용되는 연산자(선형변환)로 이해할수 있다. 행렬 곱을 통해 벡터를 다른 차원의 공간으로 변환, 패턴 추출, 데이터 압축 등 여러 연산을 시행할 수 있다.

  1. 함수(Function)

    행렬과 벡터의 곱은 열벡터의 선형결합 으로 변환되므로 입력된 벡터를 새로운 벡터로 출력하는 하나의 함수이다.

    x=[αβ],f=[2412]=>f(x)=[2412][αβ]=α[21]+β[42]\textbf{x}=\begin{bmatrix} \alpha \\ \beta \end{bmatrix}, \textbf{f}=\begin{bmatrix} 2 & 4 \\ 1 & 2 \\ \end{bmatrix}\\ =>\textbf{f(x)}= \begin{bmatrix} 2 & 4 \\ 1 & 2 \\ \end{bmatrix} \begin{bmatrix} \alpha \\ \beta \end{bmatrix} =\alpha\begin{bmatrix} 2 \\ 1 \end{bmatrix}+\beta\begin{bmatrix} 4 \\ 2 \end{bmatrix}

📄 역행렬(Inverse matrix)은 무엇인가요?

어떤 행렬 A\textbf{A} 의 연산을 거꾸로 되돌리는 행렬을 역행렬이라 부르고 A−1\textbf{A}^{-1} 라 표기한다. 주목해야할것은 행과 열 사이즈가 같고 행렬식(Determinant)이 0이 아닌 경우에만 계산할 수 있다.

📄 역행렬은 어떻게 구하나요?

다음과 같이 가우스 소거법(Gauss Elimination) 과 가우스-조던 소거법(Gauss-Jordan Elimination) 을 이용하여 구할수 있다.

numpy 에서는 np.linalg.inv() 를 통해 구할수 있다.

x=np.array([[1,2],
            [3,4]])
inverse_x=np.linalg.inv(x)         
inverse_x   
#array([[-2. ,  1. ],
#       [ 1.5, -0.5]])
x@inverse_x # Identity matrix
#array([[1.00000000e+00, 1.11022302e-16],
#       [0.00000000e+00, 1.00000000e+00]]

📄 역행렬을 계산할수 없다면 어떻게 할까요?

실제로 부딪히는 대부분의 문제는 n>m(데이터의 개수가 변수개수 보다 많은 경우,Overdetermined system) 인 경우로 Ax=bA\textbf{x}=\textbf{b} 를 만족하는 해도 A의 역행렬도 존재하지 않는다. 이럴 경우에는 A의 pseudo inverse(Moore-Penrose inverse, 무어-펜로즈 역행렬) 를 이용하여 x\textbf{x} 를 근사적으로 구하여 b\textbf{b} 에 근접하는 b^\widehat{\textbf{b}} 을 구한다.

또한 n<m(데이터의 개수가 변수 개수보다 작은경우,Underdetermined system) 인경우 무어-펜로즈 역행렬을 이용하여 해를 하나 구할 수 있다.

  • n>m

  • n<m

📚 Reference

Pseudo inverse

profile
느린 개발자
남들보단 느리지만, 끝을 향해
이전 포스트

[부스트캠프 AI Tech] U-stage. 1-5

다음 포스트

[부스트캠프 AI Tech] U-stage. 2-2

post-custom-banner

0개의 댓글