📌 DL Basics
📌 RNN(Recurrent Neural Networks)
📄 Sequential Model
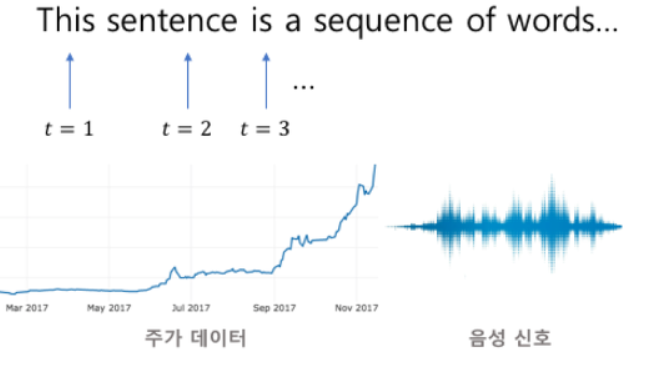
Sequence 데이터 는 음성, 자연어(Natural Language) , 주가 등 연속적인(Sequential) 시계열(Time Series) 데이터다.. 따라서, 과거 정보 또는 앞 뒤 맥락 없이 미래를 예측하는 것이 어렵고, i.i.d(Independent Identically Distribution) 를 잘 위배하기 때문에 순서가 바뀌거나 과거 정보에 손실이 발생하면 데이터의 확률분포도 바뀌게 된다. 그렇다면 어떻게 과거의 정보를 활용하여 앞으로 발생할 데이터의 확률분포를 알 수 있을까?
우리가 다루고자 하는 결합확률분포 는 다음과 같이 조건부 확률로 표현할 수 있다.
즉, 로 과거의 정보를 담은 확률분포를 표현할 수 있다.
✏️ Naive Squence Model
가장 간단한 sequential model 은 이 전의 모든 정보를 담는 방법일 것이다. 즉,
로 현 시점에서 과거의 모든 정보를 담는 모델을 정의할 수 있다.
✏️ Autogressive Squence Model
Naive Sequence Model 에서는 현 시점에서 과거의 모든 정보를 담았다. 그러나 어떤 경우엔 과거의 모든 정보를 활용할 필요가 없을 수도 있다. 또한 각 시점 마다 가변적인 길이의 데이터를 다루게 되므로 고정된 길이의 데이터를 다루는 문제로 재정의할 필요가 있다.즉,
로 고정된 길이 만큼의 정보를 담는 모델을 정의할 수 있다.
✏️ Markov Squence Model(First-order Autogressive Model)
Autogressive Sequece Model의 가장 간단한 모델은 "현재의 정보는 바로 이 전 단계의 과거의 정보에만 영향을 받는것이다" 라는 가정하에 정의하는 것이다. 즉,
로 고정된 길이 만큼의 정보를 담는 모델을 정의할 수 있다. 그러나 이것의 명확한 문제점은 현 시점의 정보가 단순히 바로 이전 단계의 과거 정보만을 가지고 결정된다는 가정에 있다.
✏️ Latent Autogressive Squence Model
Autogressive Sequence Model 에서 고정된 길이 를 활용하였지만, 문제에 따라 결정해야 할 하나의 변수 이다. 즉, 어떤 경우엔 모든 과거의 정보가 다 필요할 수도, 몇 개의 정보만 필요할 수도 있다. 그렇다면 고정된 길이의 데이터를 다루면서 유의미한 과거의 정보를 담는 방법은 없을까?
만약 다음과 같이,
잠재변수(Latent Variable) 를 이용하여 정의한다면, 고정된 길이의 데이터를 다루면서 유의미한 과거의 정보를 담는 모델을 정의할 수 있다. 나아가 를 신경망을 통해 반복해서 사용하여 sequence data의 패턴을 학습하는 모델이 RNN(Recurrent Neural Networks) 이다.
📄 Vanila RNN
✏️ Architecture

기본적인 RNN 구조는 과거의 정보 과 현재의 정보 를 반영하여 activation function (RNN에서는 주로 tanh) 을 지나 를 얻은 후 출력 를 얻는다. 이 과정을 시점에서도 반복하여 학습을 진행하게 된다.
주목할 것은 가중치 는 shared weights 로 모든 시점에서 공유하게 된다. shared weights 는 두가지의 이점이 있는데,
-
학습에 필요한 가중치의 수를 줄인다.
-
데이터별 시간의 길이에 유연하게 반응할 수 있다.

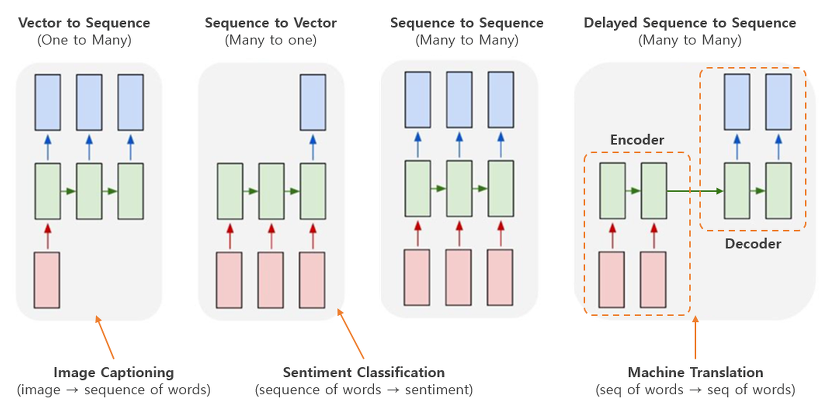
RNN이 가지는 가장 큰 이점은 input과 output의 형태에 따라 다음과 같이 다양한 구조로 RNN을 구성할 수 있다는 것이다.
✏️ BPTT(BackPropagation Through Time)
일반적으로RNN은 sequential data를 다루기 때문에 파라미터를 업데이트 하기 위해서는 이전에 사용하여 backpropagation 과는 조금은 다른 업데이트 방식이 필요하다. 이것을 BPTT(BackPropagation Through Time) 이라 부르며, 그 과정을 many-to-many 구조를 기준으로 살펴 보도록 한다.

업데이트 해야 할 가중치는 다음과 같다.
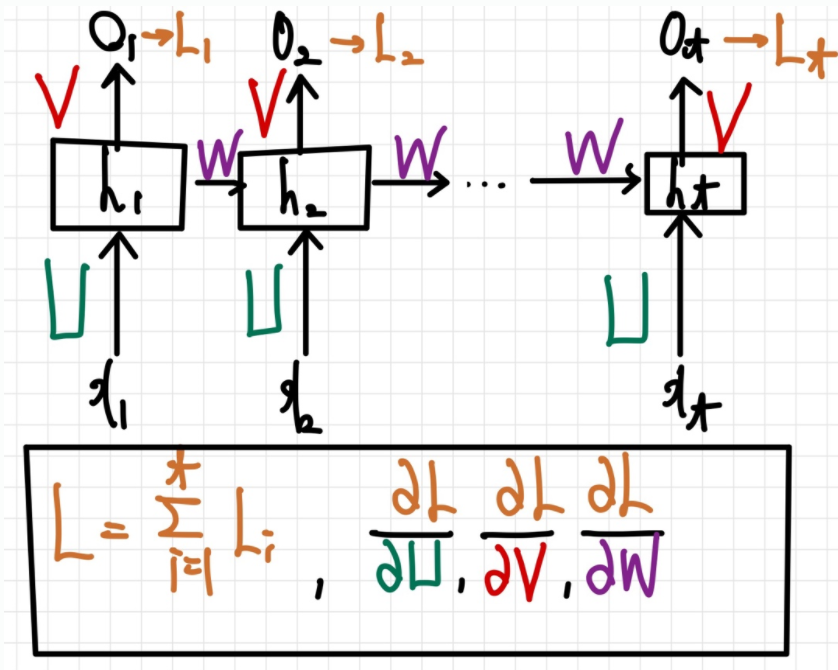
구조를 간단하게 살펴보기 위해서 인 상황을 생각해보면(그림을 간단하게 하기 위해 , 은 잠시 무시한다 ),

는 다음과 같이 간단하게 현 시점에 dependent 하게 업데이트 가능하다.
이와 동일하게 , 를 구할 수 있고 는 다음과 같다.
주목할것은 과거 정보의 영향을 받는 와 의 업데이트이다. 우선 를 살펴보면,
로 업데이트 가능할 것 같지만, 는 , 의 영향을 받기 때문에 이 전 정보들을 고려해줘야 한다. 즉,
이다. 이와 동일하게 , 을 구할 수 있고 는 다음과 같다.
역시 와 동일하게 과거 정보의 영향을 고려해야 하므로 다음과 같이 업데이트 한다.
수식으로 BPTT 를 바라보니 명확한 문제점이 보이는데, time step 이 길어질수록 멀리 있는 과거의 정보가 gradient vanishing 문제로(다음 그림을 참고) 학습내용에 기여하지 않게되고 장기의존성 문제(The problems of long-term dependencies) 를 해결하기 어렵다 는것이다.(혹자는 "tanh 대신 ReLU 함수를 사용하면 되지 않을까?" 하고 생각할 수 있겠지만, gradient exploding 문제가 발생할 수 있다.)
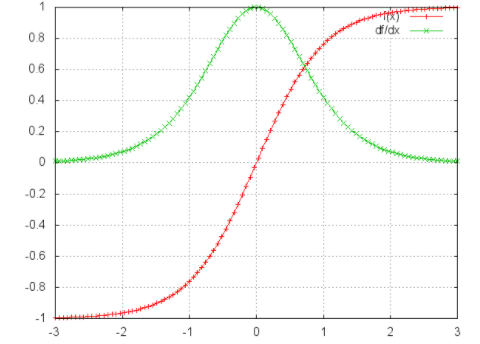
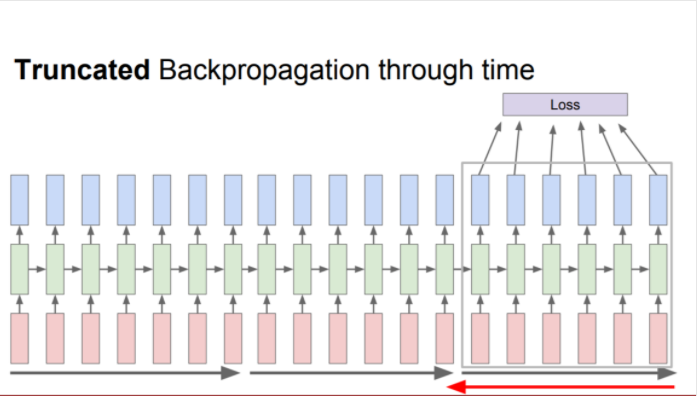
그래서 위의 문제를 개선하기 위해 전체 sequence를 일정 간격(batch 개념과 비슷)으로 잘라서(Truncated sequence) loss를 구한뒤 그에 대한 gradient를 구하는 방법이 있다.
📄 LSTM(Long Short-Term Memory)
앞서 언급했듯이, RNN 은 멀리 있는 과거 정보가 gradient vanshing 문제로 학습에 기여하지 못하는 문제가 생긴다. 이 문제를 극복하기 위해 고안된 것이 LSTM(Long Short-Term Memory) 이고 RNN의 hidden state에 cell state를 추가한 구조이다.
✏️ Architecture
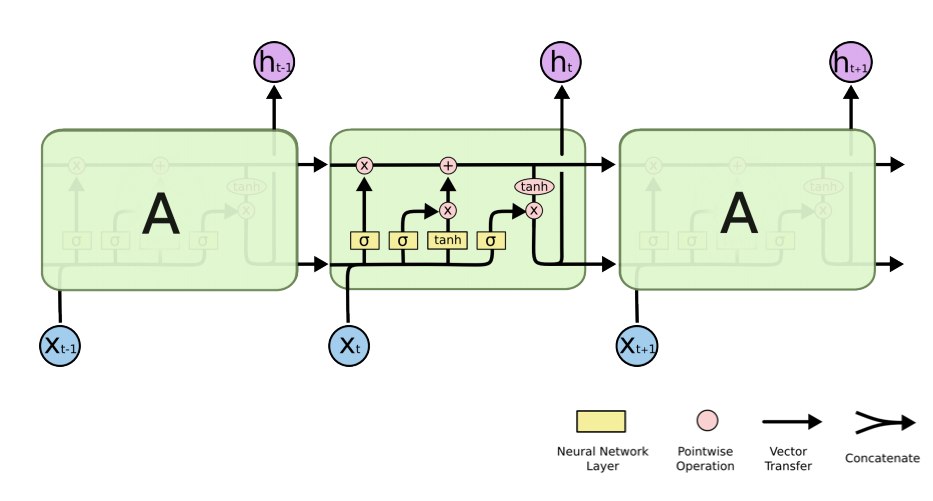
✅ Forget Gate

Forget gate 는 과거의 정보를 얼마나 반영할지를 결정하는 게이트 이다. 이전 hidden state 과 현 시점 입력 를 받아 sigmoid를 취해준 값이다. 즉, (0,1) 의 값을 갖는 sigmoid 가 과거의 정보를 얼마나 반영할지를 결정하며, 1에 가까울수록 과거 정보를 많이 / 0에 가까울수록 과거 정보를 적게 반영하게 된다.
✅ Input Gate & Candidate

Input gate 는 현시점의 정보를 셀에 얼만큼 반영할지를 결정하는 와 현 시점의 정보를 계산하는 로 이루어져 있다. 즉, 현 시점이 실제 갖고 있는 정보가 얼마나 중요한지를 반영한다.
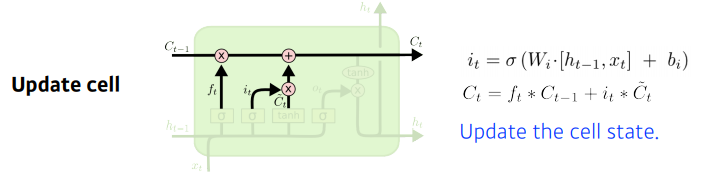
✅ Update Cell
앞서 계산한 forget gate 와 input gate 의 값을 반영하여 cell state를 업데이트 한다. 즉, 과거의 정보와 현시점의 정보의 중요도를 반영하여 업데이트 한다.
✅ Output Gate

마지막으로 output gate 는 업데이트 된 cell state(과거의 중요한 모든 정보)를 hidden state(다음 time step에 당장 필요한 정보) 로 출력할 양을 결정한다.
✅ Uninterrupted Gradient Flow

Cell state 는 forget gate ,input gate 로 정보 반영 비율을 +연산을 통해 계산된다. 즉, backpropagation 연산시 + 은 gradient를 그대로 전파해주어 gradient vanishing/exploding 문제를 해결한다.
📄 GRU(Gated Recurrent Unit)
GRU 는 LSTM 과 유사하지만 cell state 없이 더 간략한 구조를 띄고 있다. LSTM 을 제대로 이해했다면 GRU 역시 쉽게 이해할 수 있다.
<참고>
GRU 는 뉴욕대의 교수로 계시는 한국인 조경현 교수님께서 2014년에 발표한 논문에 처음 소개 되었다.
✏️ Architecture
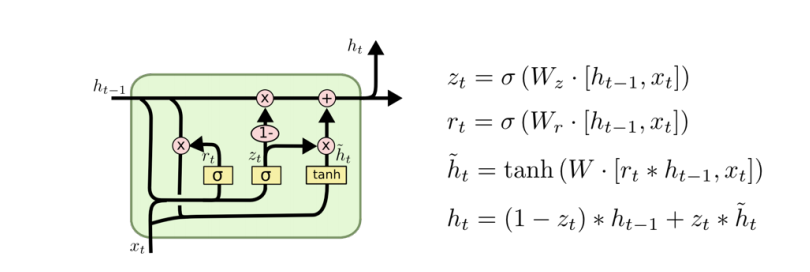

LSTM 과의 차이점은 cell state 의 역할을 가 같이 수행하고 있다는 점이다. 즉, 의 forget gate 와 input gate 의 역할을 의 가중평균으로 대체하였다. 따라서, GRU는 두개의 독립적인 gate를 한 개의 gate로 줄였다는 점에서 계산량과 메모리에 있어 이점이 있다.
✅ Reset Gate
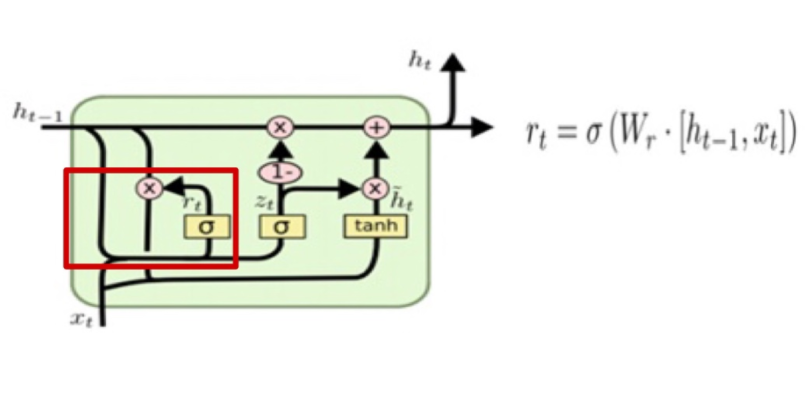
Reset gate 는 과거의 정보를 적당히 리셋시키는 게이트로 새로운 입력을 이전 hidden state와 어떻게 합칠지를 결정해준다.
✅ Update Gate
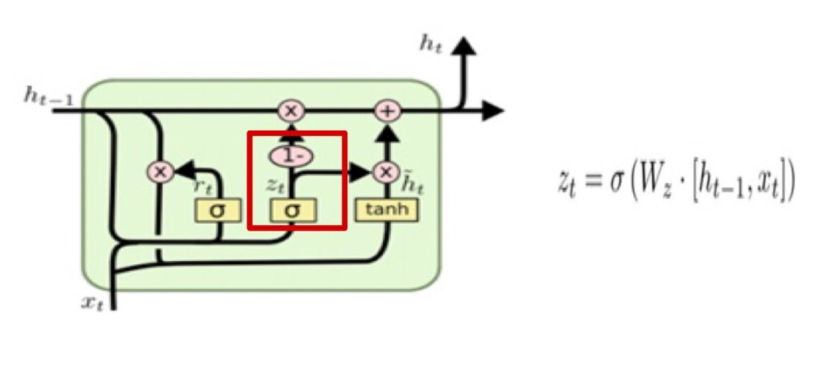
Update get는 LSTM의 forget gate+input gate 로 과거와 현재의 정보를 얼만큼 반영할지 결정하는 게이트 이다. sigmoid로 출력된 는 현시점 정보의 중요도하고 는 현 시점 정보의 중요도에 따른 과거 정보의 중요도를 결정한다.
✅ Candidate
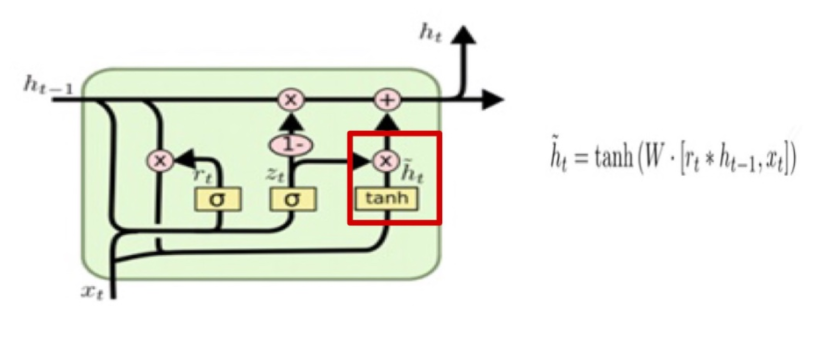
과거의 정보를 적당히 리셋시킨 reset gate의 결과를 이용하여 현시점의 정보 candidate을 계산한다.
✅ Update Hidden State
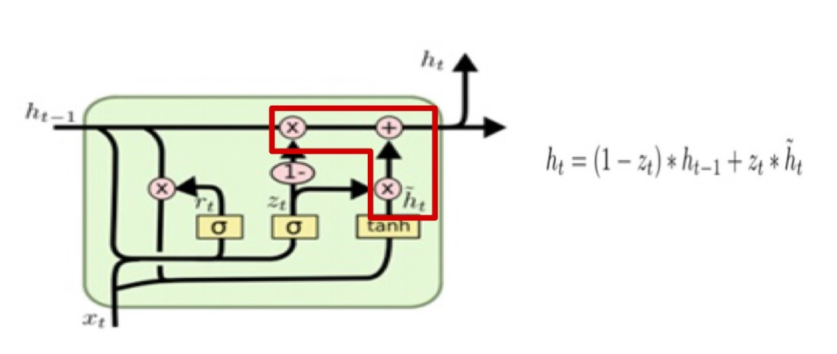
Candidate 와 Update gate 의 결과를 이용하여 현시점의 hidden state 정보를 업데이트 한다.
