📌 ML With Graphs

---

📄 Graph란 무엇인가?

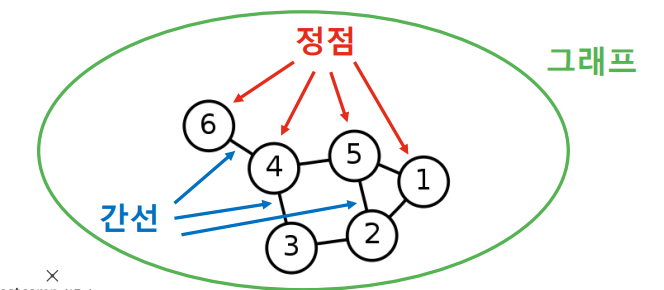
Graph(Network) 란 정점(Vertex,Node)의 집합=$V$과 간선(Edge,Link) 의 집합=$E$ 으로 이루어진 수학적 구조 $G=(V,E)$이다. 그렇다면 그래프 구조를 알아야 하는 이유는 무엇일까?

한 예로, 우리가 살아가고 있는 사회를 생각해본다면 70억인구로 구성된 복잡계(complex system) 이다. 이 외에도 통신시스템, 정보와 지식, 뇌, 신체등 여러 구조들을 복잡계로 생각할 수 있다. 이것들이 가지는 공통적인 특성에는 구성 요소간의 복잡한 상호작용 에 있다.즉, 이런 복잡계를 효율적으로 표현하고 분석하기 위해 그래프 구조가 필요한 것이다.

---

📄 Graph 관련 문제는 무엇이 있는가?

Graph 관련 인공지능 문제를 크게 분류하여 예시와 함께 살펴보면 다음과 같다.

1. Node Classification

• 트위터에서 retweet 관계를 분석하여 각 사용자의 정치적 성향을 알 수 있을까?

• 단백질의 상호작용을 분석하여 단백질의 역할을 알아낼 수 있을까?

2. Link Prediction

• 페이스북 소셜네트워크는 어떻게 진화할까? 더 줄어들까? 더 늘어날까?

3. Recommendation

• 각자에게 필요한 물건은 무엇일까? 어떤 물건을 구매해야 만족도가 높을까?

4. Community Detection

• 연결관계로 부터 사회적 무리(Social Circle)을 찾아낼 수 있을까?

5. Ranking & Information Retrieval

• 웹이라는 거대한 그래프로부터 어떻게 중요한 웹페이지를 찾아낼 수 있을까?

6. Information Cascading & Viral Marketing

• 정보는 네트워크를 통해 어떻게 전달될까? 어떻게 정보 전달을 최대화 할 수 있을까?

---

📄 Graph 기본 용어 정리

✏️Undirected Graph vs Directed Graph

✅ Undirected Graph

Edge에 방향이 없는 그래프, 즉 $(v_i,v_j)=(v_j,v_i)$ 로 순서 또는 방향이 영향을 끼치지 않는 구조이다.

• 협업 관계 그래프

• 페이스북 친구 그래프

✅ Directed Graph

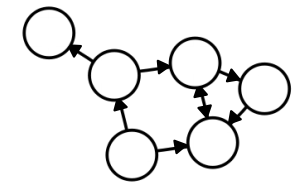
Edge에 방향이 있는 그래프, 즉 $(v_i,v_j)\not=(v_j,v_i)$ 로 순서 또는 방향이 영향을 끼치는 구조이다.

• 인용 그래프

• 트위터 팔로우 그래프

✏️Unweighted Graph vs Weighted Graph

분석하고자 하는 문제에 dependent 하여 크게 두 정점 사이의 관계에 가중치가 의미가 있는 경우 / 의미가 없는 경우로 분류할 수 있다.

✅ Unweighted Graph

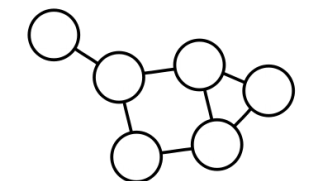
두 정점 사이의 관계에 가중치를 부여할 순 있지만 큰 의미가 없는 경우 단순화하여 표현한다.

✅ Weighted Graph

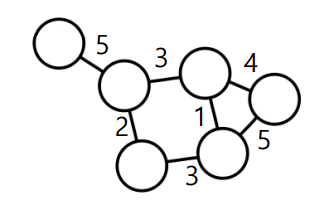
두 정점 사이의 관계에 가중치가 큰 의미가 있는 경우 표현한다.

• 전화 그래프(몇번 전화를 주고 받았는지를 가중치로 표현)

• 유사도 그래프

✏️Unpartite Graph vs Bipartite Graph

✅ Unpartite Graph

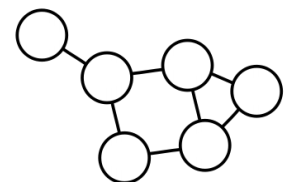
단일 종류의 정점을 가지는 그래프다.

✅ Bipartite Graph

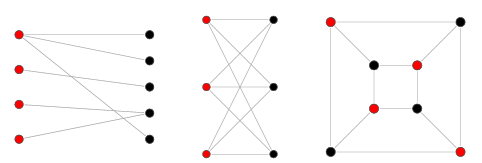
두 종류의 정점을 가지는 그래프로 서로 다른 종류의 정점사이에만 간선이 연결된다. 즉, 그래프의 모든 정점이 두 그룹으로 나눠지고 서로 다른 그룹의 정점만이 간선으로 연결되어 같은 그룹에 속한 정점끼리는 서로 인접하지 않도록 하는 그래프이다.

Bipartite graph는 Hyper Graph(Hyper-edge 가 존재하는 graph)를 쉽게 표현할수 있도록 해준다.(여기서 hyper-edge 란 하나의 edge가 2개보다 많은 vertex에 연결되어 있는 edge를 의미한다.)

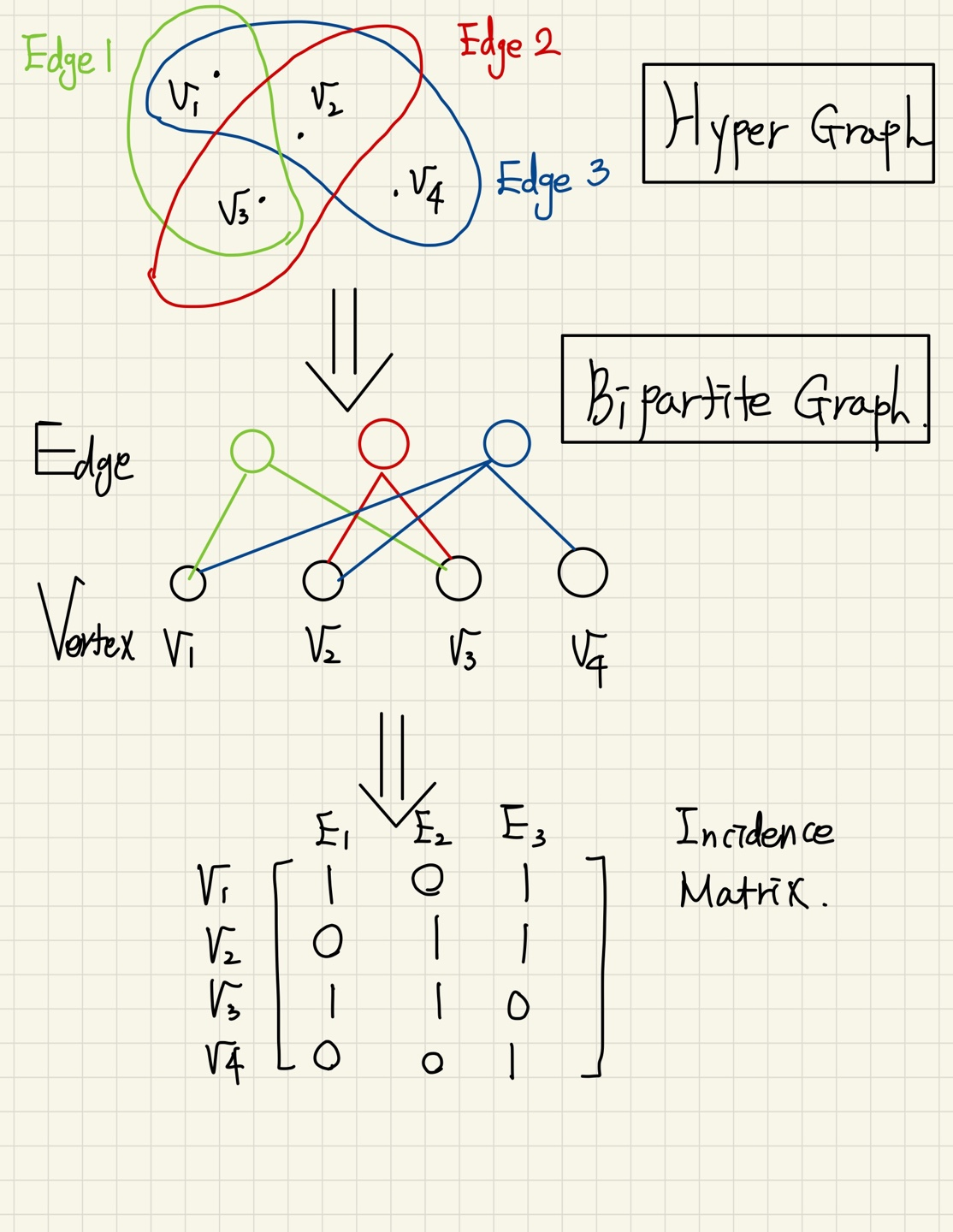
또한 일반적으로 다음과 같은 구조에 사용된다.

• 전자 상거래 구매내역(사용자,상품)

• 영화 출연 그래프(배우,영화)

✏️ Neighbor / In-neighbor / Out-neighbor

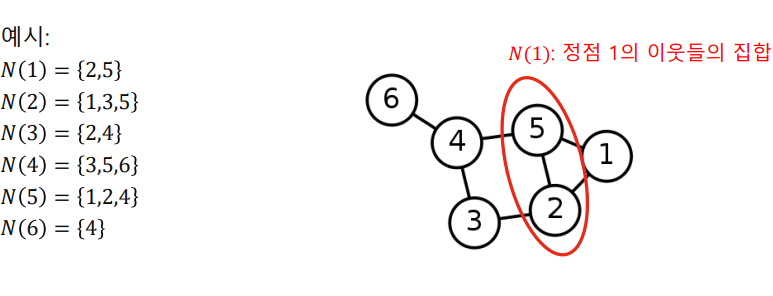
✅ Neighbor

Neighbor 는 정점과 연결된 다른 정점을 의미한다. 일반적으로 정점 $v$ 의 이웃들의 집합을 $N(v)$ 혹은 $N_v$ 로 표현한다.

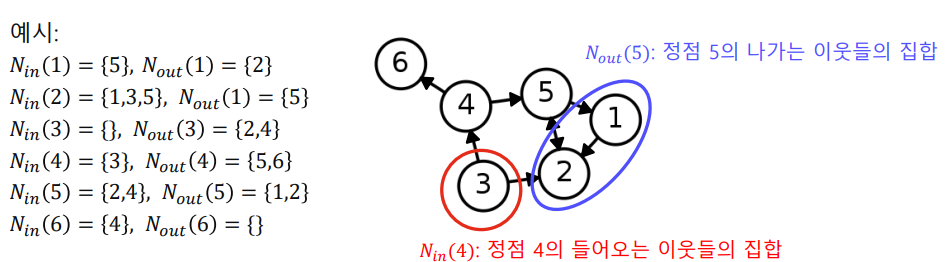
✅ In-neighbor vs Out-neighbor

Directed graph에서는 나가는 이웃(Out-neighbor) 과 들어오는 이웃(In-neighbor)을 구분하는데, 일반적으로 나가는 이웃을 $N_{out}(v)$ / 들어오는 이웃을 $N_{in}(v)$ 로 표현한다.

✏️ Path / Distance / Diameter

✅ Path

두 정점 $v_i$ 와 $v_j$의 경로(Path) 는 다음 두 조건을 만족하는 vertex 들의 순열(sequence) 이다.

1. $v_i$ 를 시작점으로 하여 $v_j$ 가 마지막 점이어야 한다.

2. 순열(sequence)에서 연속된 vertex들은 edge로 연결되어 있어야 한다.

이때, edge가 겹치지 않는 경로를 simple path / vertex가 겹치지 않는 경로를 elementry path 라고 한다.

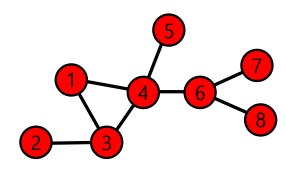
예를 들어, $v_1$ 에서 $v_8$ 의 path는 다음과 같다.

• 1 -> 4 -> 6 -> 8 : path & simple path & elementry path
• 1 -> 3 -> 4 -> 6 -> 8 : path & simple path & elementry path
• 1 -> 4 -> 3 -> 4 -> 6 -> 8 : path & not simple path & not elementry path
• $\dots$

이때,경로의 길이는 다음과 같이 해당 경로 상에 놓이는 edge의 수 $|E|=|V|-1$ 로 정의 된다.

• 1 -> 4 -> 6 -> 8 : $|E|=|V|-1=4-1=3$
• 1 -> 3 -> 4 -> 6 -> 8 : $|E|=|V|-1=5-1=4$
• 1 -> 4 -> 3 -> 4 -> 6 -> 8 : $|E|=|V|-1=6-1=5$

path가 아닌 경우는 다음과 같다.

• 1 -> 6 -> 8 : not path

• 1 -> 3 -> 4 -> 5 -> 6 -> 8 : not path

• $\dots$

✅ Distance

두 정점 $v_i$ 와 $v_j$ 사이의 거리(Distance) 는 $v_i$ 와 $v_j$ 의 shortest path의 길이이다.

위의 예시에서 $v_1$ 과 $v_8$ 사이의 shortest path 는 1 -> 4 -> 6 -> 8 이므로 distance 는 3 이다.

✅ Diameter

Graph의 diameter는 각 정점간의 distance의 최댓값으로 정의된다.

위의 예시에선 $v_2$ 와 $v_8$ 간의 distance 즉, shortest path 2 -> 3 -> 4 -> 6 -> 8의 길이가 최댓값으로 diameter 는 4 이다.

✏️ Degree / In-degree / Out-degree

✅ Degree

Vertex의 연결성(Degree) 은 해당 vertex와 연결된 edge의 수 이며 일반적으로 $d(v)$,$d_v$,$|N(v)|$ 로 표현된다.

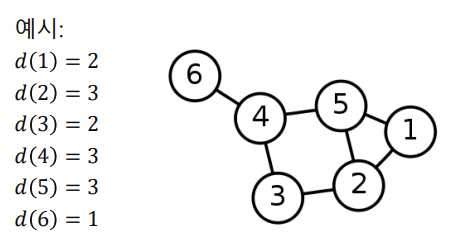
추가적으로 Handshaking Theorem 에 의해 만약 undirected graph 라면 $\sum_vd(v)=2|E|$ 이다.

✅ In-degree vs Out-degree

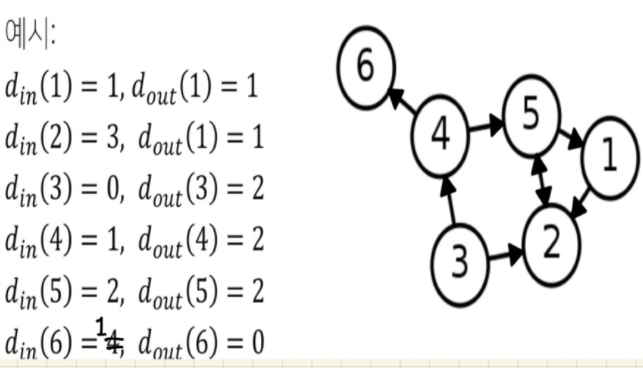
이름에서 알수 있듯이, in-degree 는 해당 vertex로 들어오는 간선의 수를 / out-degree 는 해당 vertex에서 나가는 간선의 수로 정의되며 in-degree 는 $d_{in}(v)$ 또는 $|N_{in}(V)|$ / out-degree 는 $d_{out}(v)$ 또는 $|N_{out}(V)|$ 으로 표현된다.

✏️ Connected Component

연결요소(Connected Component) 는 다음 조건들을 만족하는 vertex들의 집합이다.

1. 연결요소에 속하는 vertex들은 path로 연결될 수 있다.

2. (1)의 조건을 만족하면서 vertex를 추가할 수 없다.

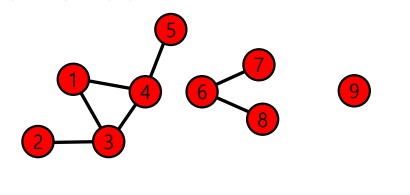
위의 그래프에는 3개의 연결요소 {1,2,3,4,5},{6,7,8},{9} 가 있다. 혹자는 {1,2,3,4} 와 {6,7,8,9} 도 연결요소라고 생각할 수 있지만 다음과 같은 이유로 연결요소가 아니다.

• {1,2,3,4}는 (1)의 조건을 만족하고 있지만, (2)번의 조건을 만족하지 않는다. 즉, vertex {5} 가 추가된다고 가정한다면 (1)의 조건을 만족하면서 vertex를 추가할 수 있기 때문이다.

• {6,7,8,9}는 (1)의 조건을 만족하지 않는다. 즉, {9} 는 path로 연결 되지 않는다.

✏️ Community / Local Clustering Coefficient / Global Clustering Coefficient

✅ Community

군집(Community)이란 다음 조건들을 만족하는 vertices 집합이다.(수학적으로 엄밀한 정의가 아니다.)

1. 집합에 속하는 vertices 사이에는 많은 edge 가 존재한다.

2. 집합에 속하는 vertices 와 그렇지 않은 vertices 에는 적은 수의 edge가 존재한다.

✅ Local Clustering Coefficient

해당 vertex 에서 community의 형성정도를 측정하는 척도로 다음과 같이 정의된다.

• $c_i$= i번째 vertex $v_i$의 clustering coefficient
• $e_i$= $N_{v_i}$ 의 edge 수
• $k_i$= $v_i$ 의 degree

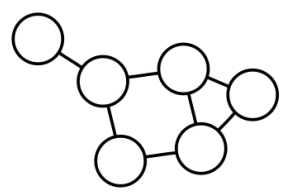
다음의 예시에서,

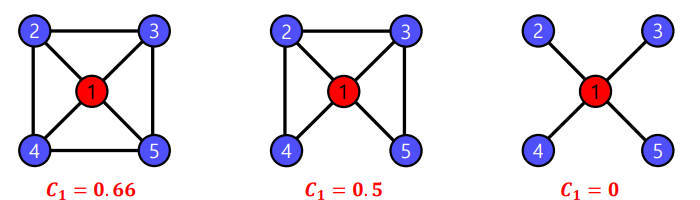
가운데를 기준으로 설명한다면 $v_1$ 의 이웃은 4개이며, 총 $\binom{4}{2}$개의 이웃쌍이 존재한다. 이때 3개의 쌍 (2,3),(2,4),(2,5)는 edge로 직접 연결되어 있다. 따라서 local clustering coefficient $c_1=\frac{3}{6}=0.5$ 이다. 또한 위의 예시를 통해 $C_i$ 가 0에 가까울수록 주변 노드들이 해당노드를 통해서만 연결되어 있는 것이고, 1에 가까울수록 해당 노드 없이도 주변 노드끼리 충분히 연결되어 있다는것을 확인할 수 있다.

<참고>
Degree가 0 /1 인 경우 vertex에서는 정의되지 않는다. 다만 상황에 따라 degree 가 2 미만인 vertex에 대해 local clustering coefficient를 0 으로 정의하는 경우도 있다.

✅ Global Clustering Coefficient

전체 그래프에서 community의 형성 정도를 측정하는 척도로 각 vertex에서 local clustering coefficient의 평균이다.

---

📄 Graph 를 어떻게 표현할까?

✏️ Edge List vs Adjacent List vs Adjaceny Matrix

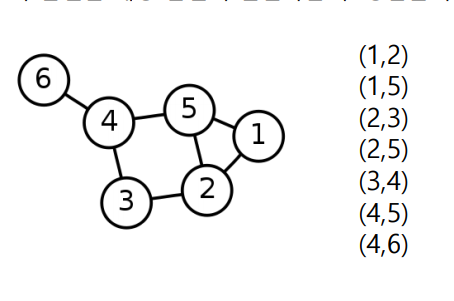
✅ Edge List(Undirected Graph)

각 간선은 해당 간선이 연결하는 순서가 상관없는 두 정점들의 쌍 으로 표현된다. 즉 $(v_{i},v_{j})=(v_{j},v_{i})$ 의 성질을 가진다.

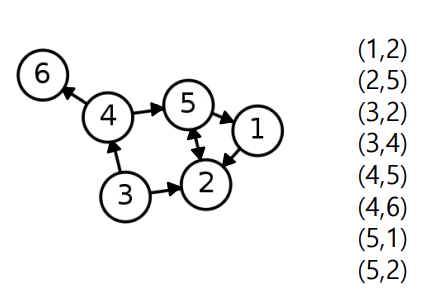
✅ Edge List(Directed Graph)

방향성이 있는 경우 (src,dst) 로 순서가 의미 있는 두 정점들의 쌍 으로 표현된다. 즉 $(v_{i},v_{j})\not=(v_{j},v_{i})$ 의 성질을 가진다.

✅ Adjacent List(Undirected Graph)

Edge List 의 경우 해당 노드의 간선을 찾기 위해서 순차적으로 접근해야 하는 문제가 생긴다. 그래서 인접한 노드들을 모아서 표현하여 빠르게 접근할수 있도록 Adjacent List를 이용한다.

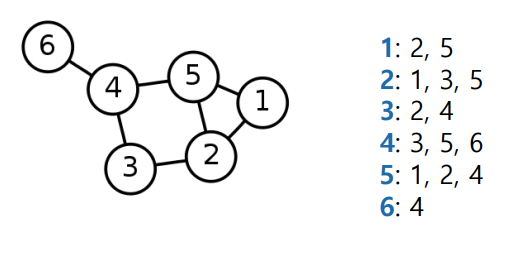
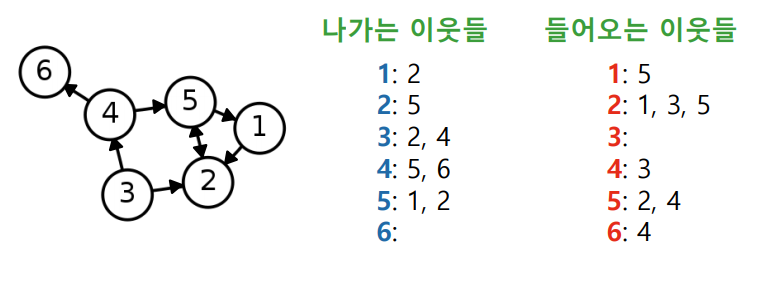
✅ Adjacent List(Directed Graph)

방향성이 있는 경우 in-neightbor 과 out-neighbor 를 나누어서 각각 저장한다.

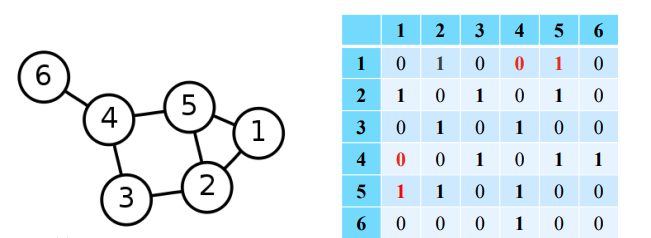
✅ Adjacency Matrix(Undirected Graph)

$|V|$x$|V|$ 의 크기를 가지는 matrix로 $v_i$ 와 $v_j$ 사이에 간선이 있는 경우 $v_{ij}=1$ / 없는 경우 $v_{ij}=0$ 의 값을 가진다. 또한 방향성이 없는 그래프에서는 symmetric matrix로 표현된다.

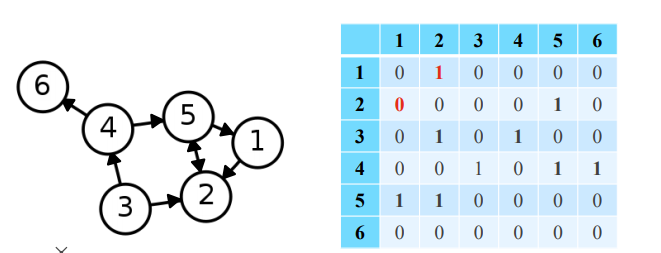
✅ Adjacency Matrix(Directed Graph)

방향성이 없는 경우와의 유일한 차이점은 symmetric matrix가 아닐수도 있다는 것이다.

---

📄 Real Graph를 어떻게 분석할까?

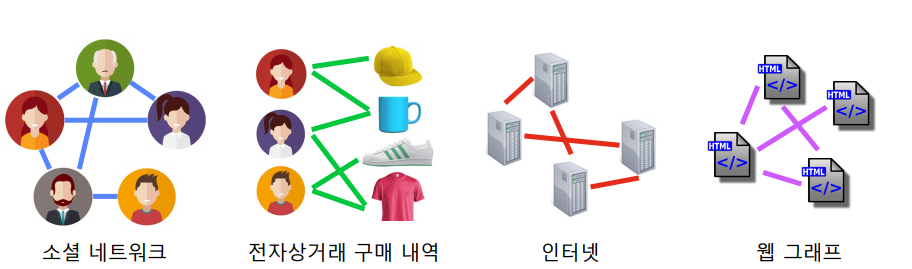
실제 그래프(Real Graph) 란 다양한 complex system으로 부터 얻어진 그래프를 의미한다. 우리의 목적은 실제 그래프를 예측하고 분석하는 것이지만 사실상 어떻게 구성되어 있는지 확인하기 어렵고, 분석하는것이 매우 어렵다. 그래서 network(graph) modeling 을 통해 간단한 형태의 모델을 만들어 실제 네트워크에서 발생하게 될 일들을 예측하고 분석하려 한다. 이때 실제 그래프가 가지는 다양한 패턴들을 알고 비교해보는것은 network modeling 에 도움이 될것이다.

✏️ Random Graph

Random Graph 란 network modeling 중 하나로 확률적 과정을 통해 생성한 그래프를 의미한다. 여기서는 Erdős–Rényi model 을 이용하여 살펴보도록 한다.

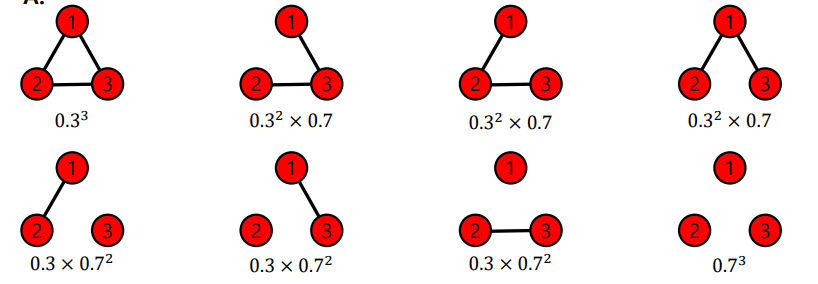
Erdős–Rényi model=G(n,p) 은 임의의 두 노드 사이에 엣지가 존재하는지의 여부는 동일한 확률분포로 결정한다. 즉, n개의 노드들이 있다고 가정했을때 임의의 두개의 노드 사이에 엣지가 존재할 확률은 p이며 노드사이의 연결은 서로 독립적이라고 가정한다. 이해를 돕기 위해 G(3,0.3) 인 random graph를 생각해보면 다음과 같다.

즉 생성될 수 있는 그래프는 총 $\sum^n_{i=1}\binom{n}{k}$개가 있으며 각 그래프는 $p^k(1-p)^{n-k}$ 의 확률을 따른다.

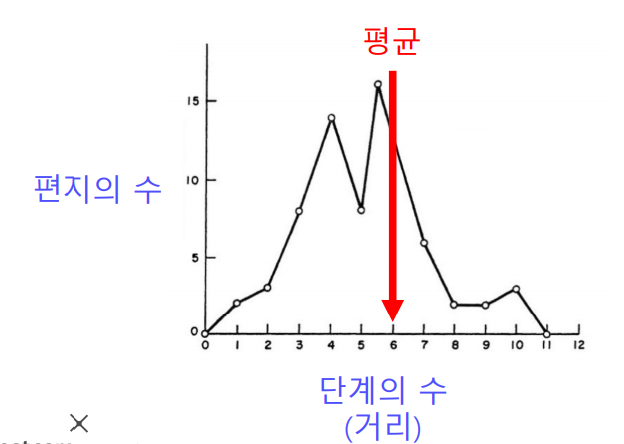
✏️ Small World Effect

Small World Effect는 사회학자 스탠리 밀그램(Stanley Milgram)에 의해 1960년대에 수행된 여섯 단계 분리(Six Degrees Of Separation) 실험에서 나온 용어이다. 실험의 내용을 간단하게 살펴보면, 오마하 (네브라스카 주)와 위치타 (켄사스 주)에서 500명의 사람을 뽑아 그들에게 보스턴에 있는 한 사람에게 편지를 전달하게끔 하였다.(단, 지인를 통해서만 전달이 가능하다.) 이 실험의 목적은 "목적지에 도착하기 까지 몇 단계의 지인을 거쳤을까?" 를 파악하는것이었는데, 결과는 다음과 같이 평균적으로 6단계만을 거쳐서 전달되었다는 것이다. 즉 "엄청난 크기의 네트워크에서도 비교적 적은 수의 단계로 연결이 된다"는 것을 의미한다.

Small world effect는 실제 그래프 뿐만이 아니라 랜덤 그래프에서도 높은 확률로 나타나는데 직관적으로 생각하면 다음과 같다.

1. 모든 사람이 100명 의 지인이 있다고 가정한다.

2. 다섯단계를 거치면 최대 100억($100^5$)명의 사람과 연결될 수 있다.

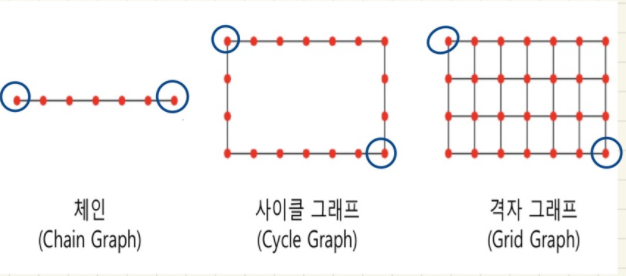
하지만 모든 그래프에서 small world effect가 존재하는 것은 아니다. 가령 Chain Graph,Cycle Graph,Grid Graph 의 경우 네트워크의 크기가 커짐에 따라 정점 사이의 거리 역시 멀어진다.

✏️ Degree Distribution

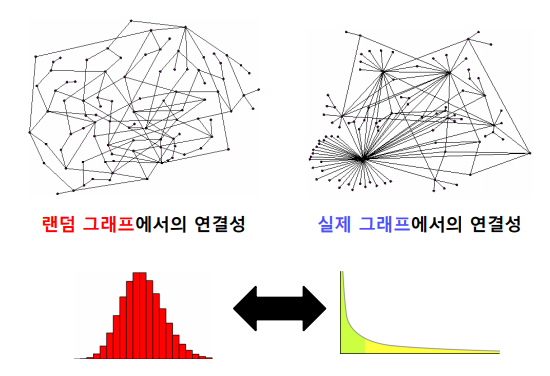
실제 그래프에선 degree가 매우 높은 hub node가 존재하는 heavy tail 꼴의 degree distribution 이 나타난다. 즉, degree가 낮은 노드의 수가 많고 degree 가 높은 노드의 수가 적다. 예를들어, SNS의 팔로워 수가 많은 계정(degree가 매우 높은 hub node) 과 팔로워 수가 적은 계정 (degree가 낮은 노드) 을 생각해본다면 쉽게 이해할수 있을 것이다.

반면 랜덤그래프에선 높은 확률로 normal distribution과 유사하다. 즉 degree 가 매우 높은 hub node 가 존재할 가능성은 적다. 이것은 조금만 생각해본다면 이해할 수 있는데, 우선 다음과 같이 확률 $P_k$ 을 정의한다.

그러면 다음과 같이 $P_k$는 구해진다.

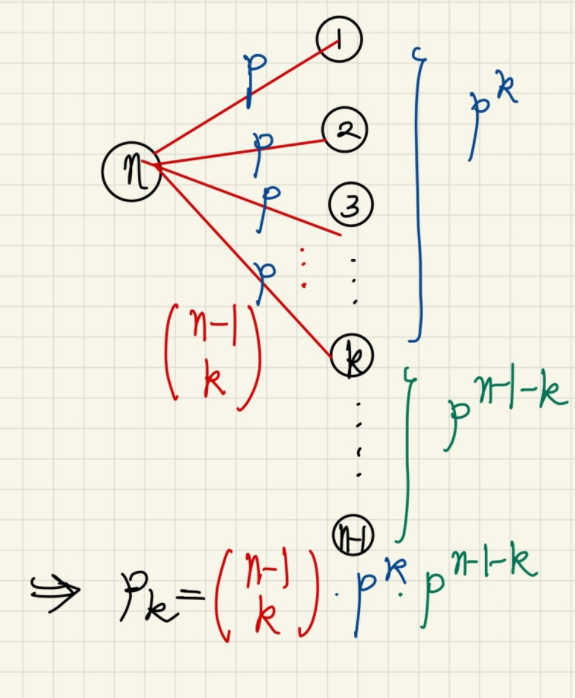
따라서 $P_k$ 는 binomial distribution 이며 Normal Approximation 에 의해 normal distribution으로 근사시킬 수 있다.

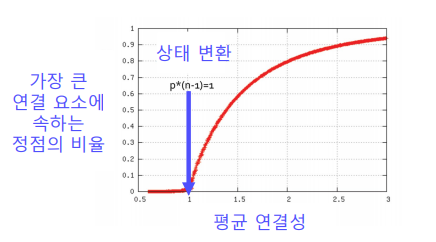
✏️ Giant Connected Components

실제 그래프에는 거대 연결 요소(Giant Connected Component) 가 존재하여 대다수의 노드를 포함하고 있다.

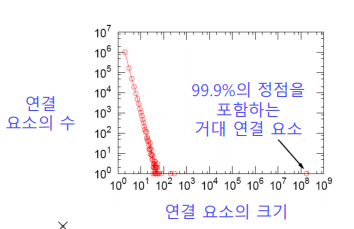
랜덤 그래프에도 높은 확률로 거대 연결요소가 존재하는데 vertex의 평균 degree가 1보다 충분히 커야 한다.(수학적 증명은 여기를 참고하도록 한다.)

✏️ Clustering Coefficient

실제 그래프에선 군집 계수가 높다. 이러한 이유는 여러가지가 있겠지만 크게 두가지를 살펴보면 다음과 같다.

1. 동질성(Homophily)
   서로 유사한 노드끼리 엣지로 연결될 가능성이 높다. 예를 들어 같은 동네에 사는 같은 나이의 아이들이 친구가 되는 경우이다.

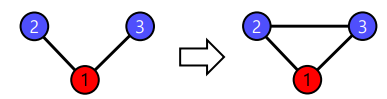
2. 전이성(Transivity)
   공통이웃이 있는 경우, 공통 이웃이 매개역할을 해줄 수 있다. 예를 들어 친구를 서로에게 소개해주는 경우이다.

반면 랜덤그래프에서는 지역적 혹은 전역 군집 계수가 높지 않다. 그 이유는 다음에서 하나씩 살펴보도록 한다.

Random graph $G(n,p)$ 에서 n과 p가 주어졌을때, graph가 생성될때마다 항상 edge의 개수는 달라지지만 이것은 특정확률 p 를 따르기 때문에 평균 edge의 개수 $\bar m$ 를 구할수 있다. 그래서 edge개수가 m 개인 random graph 하나가 생성될 확률을 생각해본다면, 다음과 같다.

즉, edge가 연결될 2개의 후보군 노드 $\binom{n}{2}$ 에서 m개의 엣지가 연결될 노드의 개수는 $\binom{\binom{n}{2}}{m}$ 이다. 이때, m개의 노드가 연결되고 $\binom{n}{2}-m$ 개의 노드가 연결되지 않을 확률은 $p^m(1-p)^{\binom{n}{2}-m}$ 이다. 따라서 $P(m)=\binom{\binom{n}{2}}{m}p^m(1-p)^{\binom{n}{2}-m}$ 이다. 주목할것은 m의 확률 분포가 binomial distribution을 따른다는것이고, 따라서 $\bar m=\binom{n}{2}p=\frac{n(n-1)}{2}p$ 임을 쉽게 알 수 있다.

Clustering coefficient를 구하기 위해서 또 한가지 알아야할 것은 노드의 degree 인데 이 역시 graph가 생성될때마다 항상 degree가 달라지므로 평균 degree $\bar k$ 를 구하도록 한다. 이때, 평균 degree $\bar k$ 라는 것은 한 vertex에서 가지는 평균 edge의 개수를 의미하는 것이므로 평균 edge의 개수 $\bar m$ 을 $\frac{n}{2}$($\because(v_i,v_j)= (v_j,v_i)$) 로 나눠준 $\bar k=(n-1)p$ 임을 직관적으로 알 수 있다.

위의 두 결과를 바탕으로 local clustering coefficient $c_i=\frac{e_i}{\binom{k_i}{2}}$ 의 기댓값 $E[C]$ 은

임을 확인할 수 있다. 즉, 실제 그래프에선 네트워크의 수가 커짐에도 불구 하고 군집계수가 높게 유지되는 성질을 가지는 반면 랜덤그래프에선 네트워크의 수 (n) 이 커짐에 따라 군집계수가 낮아지게 된다.

✏️ Optional

Network modeling을 위해 random graph를 살펴 보았다. 이 외에도 Regular Graph, Small-world Graph,Scale-free Graph 등의 대표적인 그래프들이 존재한다. 이것들을 추가적으로 공부한다면 real graph 와의 패턴의 차이(Degree distribution,diameter,clustering coefficient,$\dots$) 에 집중하여 살펴보는 것이 도움될 것이다.

---

📄 NetworkX

추후 업데이트

---

📚 Reference

Bipartite Graph
Random Graph1
Random Graph2