🏆 알고리즘 문제 풀이
📌 문제 정보
- 문제명 : 파핑파핑 지뢰찾기
- 출처 : https://swexpertacademy.com/main/code/problem/problemDetail.do?contestProbId=AV5LwsHaD1MDFAXc
- 난이도 : D4
- 유형 : BFS / DFS
🧐 문제 설명
N×N 크기의 보드에 지뢰(‘*’)와 빈칸(‘.’)이 있다.
플레이어는 한 번 클릭으로 지뢰가 없는 칸을 열 수 있다.
만약 클릭한 칸이 주변 8칸 모두에 지뢰가 없다면(0칸), 인접한 칸들이 연쇄적으로 자동 오픈된다.
👉 최소 몇 번의 클릭으로 모든 안전한 칸을 열 수 있는지 구하는 문제
💡 접근 방법
- 주변 지뢰 개수 계산
- 모든 칸에 대해 인접 8방향 지뢰 개수를 미리 세어둔다.
- 지뢰가 없는 칸만 BFS/DFS 대상으로 삼는다.
- DFS/BFS 탐색
- 숫자가 0인 칸을 클릭하면, 인접한 칸들이 자동으로 열리므로 BFS/DFS 확장한다.
- 한 번 BFS 실행하면 여러 칸이 동시에 열리므로 클릭 횟수는 1 증가한다.
- 남은 숫자 칸 클릭
- BFS로 열리지 않은 숫자 칸들은 직접 한 번씩 클릭해야 한다.
📝 풀이 과정
| 단계 | 설명 |
|---|---|
| 1 | 보드를 입력받고 인접 8칸 탐색으로 지뢰 개수를 계산 |
| 2 | 숫자가 0인 칸부터 BFS/DFS 실행 → 연쇄적으로 열리게 함 |
| 3 | BFS를 실행한 횟수만큼 클릭 횟수 증가 |
| 4 | BFS 후에도 열리지 않은 숫자 칸은 직접 클릭 (1씩 증가) |
| 5 | 전체 클릭 횟수 출력 |
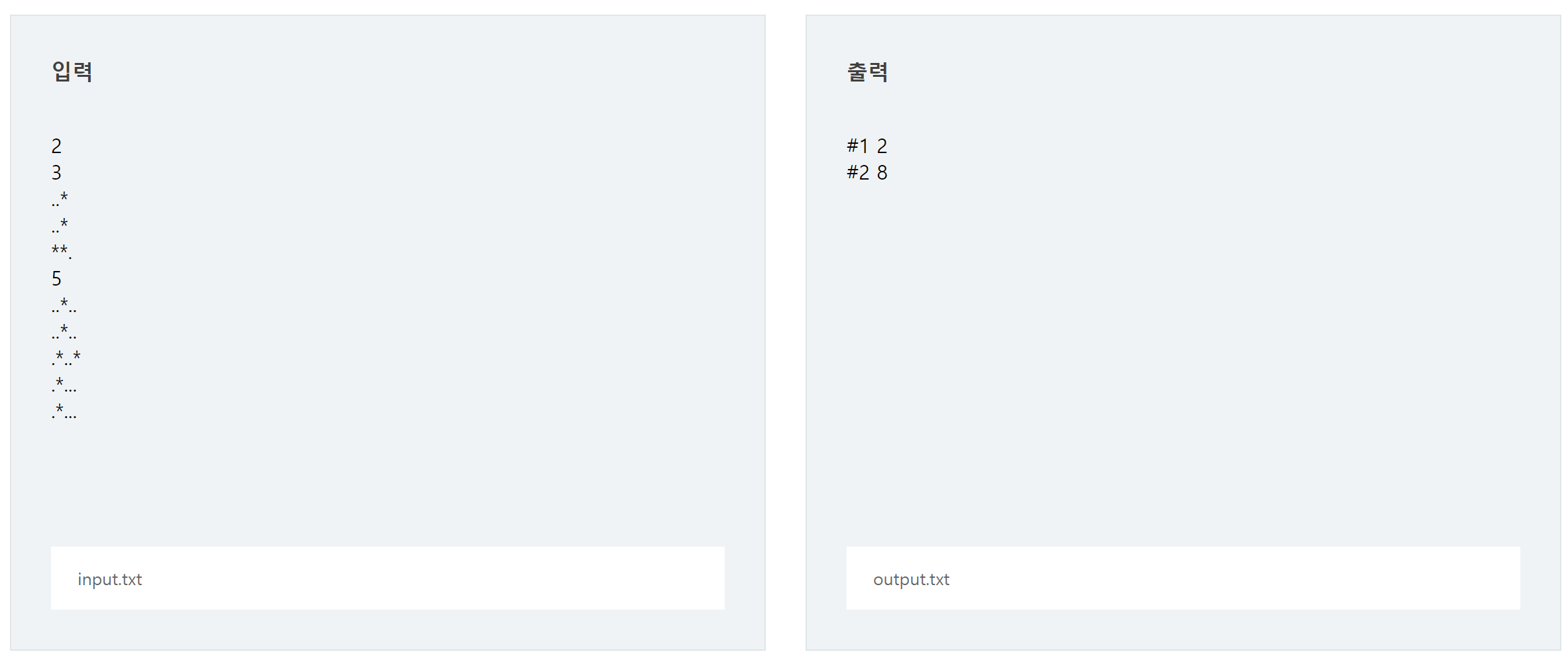
입력 & 출력 예시
🧑💻 코드
import java.util.Scanner;
public class Swea_1868_파핑파핑지뢰찾기 {
static char arr[][];
static boolean visited[][];
static int n;
static int[] dx = {-1,1,0,0,-1,-1,1,1};
static int[] dy = {0,0,-1,1,-1,1,-1,1};
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int T = sc.nextInt();
for (int tc = 1; tc <= T; tc++) {
n = sc.nextInt();
arr = new char[n][n];
visited = new boolean[n][n];
for (int i = 0; i < n; i++) {
String line = sc.next();
for (int j = 0; j < n; j++) {
arr[i][j] = line.charAt(j);
}
}
//로직
// Step1: 숫자판 만들기
makeNumberBoard();
int count = 0;
// Step2: 0칸부터 DFS 돌리기
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (arr[i][j] == '0' && !visited[i][j]) { //arr[i][j] == '0' 주변에 지뢰가 없느 빈 칸이고 아직 열리지 않은 칸이면
dfs(i, j); //연쇄적으로 주변 칸들(0과 그 주변 숫자칸들)까지 다 열어줌
count++; //0 칸 하나 클릭 = 한 번 클릭 추가
}
}
}
// Step3: 아직 방문 안 된 숫자칸 개별 클릭
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (arr[i][j] != '*' && !visited[i][j]) { //지뢰가 아니면서(!= '*'), 아직 열리지 않은 칸 == 이 칸들은 모두 숫자칸(1~8)
count++; // 0을 클릭해도 자동으로 안 열리니까 직접 클릭
}
}
}
System.out.println("#" + tc + " " + count);
}
}
// 숫자판 만들기
public static void makeNumberBoard() {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
// 지뢰 없는 칸을 눌러야 하기 때문에 (지뢰 있는 칸 누르면 게임 끝나버림)
if (arr[i][j] == '.') { // 지뢰 없는 칸이면 ..
int mineCount = 0; // 그 주변 8방향 지뢰 개수 세기
for (int d = 0; d < 8; d++) {
int nx = i + dx[d];
int ny = j + dy[d];
if (nx < 0 || nx >= n || ny < 0 || ny >= n) continue;
if (arr[nx][ny] == '*') mineCount++; //지뢰면 카운트 업
}
arr[i][j] = (char)(mineCount + '0'); // '0' ~ '8' 지뢰 개수로 값 바꾸기
}
}
}
}
public static void dfs(int x, int y) {
visited[x][y] = true;
if (arr[x][y] == '0') { // 0일 때만 주변 확장
for (int h = 0; h < 8; h++) {
int nx = x + dx[h];
int ny = y + dy[h];
if (nx < 0 || nx >= n || ny < 0 || ny >= n) continue;
if (visited[nx][ny]) continue;
dfs(nx, ny);
}
}
}
}🔍코드해설
1️⃣ 숫자판 만들기 (makeNumberBoard)
if (arr[i][j] == '.') {
int mineCount = 0;
for (int d = 0; d < 8; d++) {
int nx = i + dx[d];
int ny = j + dy[d];
if (nx < 0 || nx >= n || ny < 0 || ny >= n) continue;
if (arr[nx][ny] == '*') mineCount++;
}
arr[i][j] = (char)(mineCount + '0');
}- 지뢰(*)가 아닌 칸(.)에 대해 주변 8방향의 지뢰 개수를 센다.
- 지뢰 개수만큼 '0' ~ '8' 문자로 변환하여 보드에 기록한다.
👉 이후 DFS/BFS 탐색 시 숫자 칸인지(1~8) 또는 빈칸인지(0) 판별 가능하다.
2️⃣ DFS 탐색 (dfs)
visited[x][y] = true;
if (arr[x][y] == '0') { // 0칸일 때만 주변 확장
for (int h = 0; h < 8; h++) {
int nx = x + dx[h];
int ny = y + dy[h];
if (nx < 0 || nx >= n || ny < 0 || ny >= n) continue;
if (visited[nx][ny]) continue;
dfs(nx, ny);
}
}- 현재 칸을 방문 처리한다.
- 해당 칸이 0이면 → 주변 8칸을 재귀적으로 DFS 확장한다.
- 숫자 칸(1~8)은 더 확장되지 않고 열리기만 한다.
👉 마치 실제 지뢰찾기에서 0칸 클릭 시 주변이 한 번에 열리는 동작과 동일하다.
3️⃣ 클릭 횟수 계산 로직
// Step2: 0칸부터 DFS
if (arr[i][j] == '0' && !visited[i][j]) {
dfs(i, j);
count++;
}
// Step3: 남은 숫자칸 클릭
if (arr[i][j] != '*' && !visited[i][j]) {
count++;
}- 0칸('0') : DFS 실행 시 한 번의 클릭으로 여러 칸이 연쇄적으로 열리므로 count++.
- 숫자칸('1'~'8') : DFS로는 열리지 않으므로 직접 클릭해야 하며, 방문되지 않았다면 count++.
💭 추가
✨ BFS로도 가능
package Swea;
import java.util.ArrayDeque;
import java.util.Deque;
import java.util.Scanner;
public class Swea_1868_파핑파핑지뢰찾기_BFS {
static char arr[][];
static boolean visited[][];
static int n;
static int[] dx = {-1,1,0,0,-1,-1,1,1};
static int[] dy = {0,0,-1,1,-1,1,-1,1};
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int T = sc.nextInt();
for(int tc = 1; tc <= T; tc++) {
n = sc.nextInt();
arr = new char[n][n];
visited = new boolean[n][n];
for(int i=0; i<n; i++){
String line = sc.next();
for(int j=0; j<n; j++){
arr[i][j] = line.charAt(j);
}
}
makeNumberBoard();
int count = 0;
// Step1: 0칸부터 BFS 돌리기
for(int i=0; i<n; i++){
for(int j=0; j<n; j++){
if(arr[i][j]=='0' && !visited[i][j]){
bfs(i,j);
count++;
}
}
}
// Step2: 남은 숫자칸 직접 클릭
for(int i=0; i<n; i++){
for(int j=0; j<n; j++){
if(arr[i][j]!='*' && !visited[i][j]){
count++;
visited[i][j] = true;
}
}
}
System.out.println("#" + tc + " " + count);
}
}
public static void makeNumberBoard() {
for(int i=0; i<n; i++){
for(int j=0; j<n; j++){
if(arr[i][j]=='.'){
int mineCount = 0;
for(int d=0; d<8; d++){
int nx = i + dx[d];
int ny = j + dy[d];
if(nx<0 || nx>=n || ny<0 || ny>=n) continue;
if(arr[nx][ny]=='*') mineCount++;
}
arr[i][j] = (char)(mineCount + '0');
}
}
}
}
public static void bfs(int x, int y){
Deque<int[]> q = new ArrayDeque<>();
q.add(new int[]{x, y});
visited[x][y] = true;
while(!q.isEmpty()){
int[] cur = q.poll();
int cx = cur[0];
int cy = cur[1];
if(arr[cx][cy]=='0'){
for(int h=0; h<8; h++){
int nx = cx + dx[h];
int ny = cy + dy[h];
if(nx<0 || nx>=n || ny<0 || ny>=n) continue;
if(visited[nx][ny]) continue;
visited[nx][ny] = true;
q.offerLast(new int[]{nx, ny});
}
}
}
}
}
🌐 파핑파핑 지뢰찾기 DFS vs BFS 비교
| 구분 | DFS | BFS |
|---|---|---|
| 확장 방식 | 재귀 호출로 한 방향 깊게 들어가며 0칸 주변 확장 | 큐에 넣고 레벨 단위로 넓게 주변 0칸 확장 |
| 연쇄 오픈 순서 | 한 칸에서 가능한 최대 깊이까지 먼저 열림 → 스택 구조 느낌 | 한 칸에서 주변 0칸을 모두 큐에 넣고 차례대로 열림 → 큐 구조 느낌 |
| 방문 처리 시점 | 함수 진입 시 (visited[x][y] = true) | 큐에 넣는 순간 (visited[nx][ny] = true) |
| 숫자칸 처리 | 0 주변 DFS가 끝나면 숫자칸은 자동으로 열림 | 0 주변 BFS가 끝나면 숫자칸은 자동으로 열림 |
| 장점 | 코드 간결, 구현 쉽다 | 연쇄 오픈 순서 직관적, 큐 구조로 직관적인 레벨 탐색 가능 |
| 단점 | 스택 깊이가 깊어지면 재귀 깊이 제한 걸릴 수 있음 | 코드가 DFS보다 조금 길 수 있음 |
| 클릭 횟수 계산 | 0칸 클릭 → 재귀로 연쇄 오픈 → count 1 증가 남은 숫자칸 직접 클릭 → count 증가 | 0칸 클릭 → 큐로 연쇄 오픈 → count 1 증가 남은 숫자칸 직접 클릭 → count 증가 |
