[백준.G4] - 16929. Two Dots

Jimin Kwon·2025년 9월 28일
백준

알고리즘

목록 보기
8/13

🏆 알고리즘 문제 풀이

📌 문제 정보

🧐 문제 설명

문제에서 요구하는 것은 같은 색 점을 이어 사이클이 존재하는지 여부를 판별하는 것

  • 크기 N x M 의 격자판이 주어짐
  • 각 칸은 알파벳 소문자 중 하나로 채워져 있음
  • 상하좌우로 인접한 칸을 통해 이동 가능
  • 조건 : 같은 알파벳을 따라 이동했을 때, 사이클이 존재하는지 확인
  • 사이클은 4개 이상의 점이 연결되어 있어야 하며, 시작점과 끝점이 같아야 함

👉 출력 : 사이클이 존재하면 Yes, 존재하지 않으면 No

💡 접근 방법

  1. DFS 탐색 활용

    • 각 칸에서 출발하여 DFS로 같은 알파벳을 따라 탐색

  2. 사이클 판별 조건

    • 현재 노드에서 다음 노드로 이동할 때,
      • 같은 알파벳인지 확인
      • 직전에 방문한 노드(부모 노드)로는 되돌아가지 않도록 제외
    • 만약 이미 방문한 칸을 다시 방문했는데, 이동한 칸의 수가 4 이상이면 사이클이 존재한다고 판단

  3. 최적화

    • 방문 여부를 기록하기 위해 visited[][] 배열 사용
    • 한번 방문한 시작점에서 탐색이 끝나면 다시 방문할 필요 없음

📝 문제 설계

  • 변수

    • n, m : 격자 크기
    • arr : 문자 배열
    • visited : 방문 체크 배열
    • dx, dy : 상하좌우 이동 좌표
    • foundCycle : 사이클 발견 여부

  • 흐름

    1. 입력으로 격자 크기와 문자 배열을 받음
    2. 모든 좌표를 돌면서 방문하지 않은 곳이라면 DFS 탐색
    3. DFS 중 사이클이 발견되면 즉시 탐색 종료
    4. 최종적으로 Yes / No 출력

  • 사용 알고리즘

    • DFS
      • DFS를 이용해 탐색하면서 현재 경로에서 이미 방문한 칸을 다시 만났을 때 사이클 여부를 판별

  • 해당 알고리즘을 선택한 근거

    1. 사이클 탐지 문제에 적합

      • DFS는 방문한 노드를 추적하면서 현재 탐색 경로를 관리할 수 있어, 사이클 유무를 쉽게 판별 가능
      • 특히 이전에 방문했지만, 직전에 온 경로(부모 노드)가 아닌 곳을 다시 만나면 사이클임을 확인 가능

    2. 보드 크기가 작음

      • 보드의 크기는 최대 50 x 50 = 2500칸.
      • 모든 칸에서 DFS를 돌려도 시간 복잡도는 O(N*M*4) 정도로 충분히 해결 가능

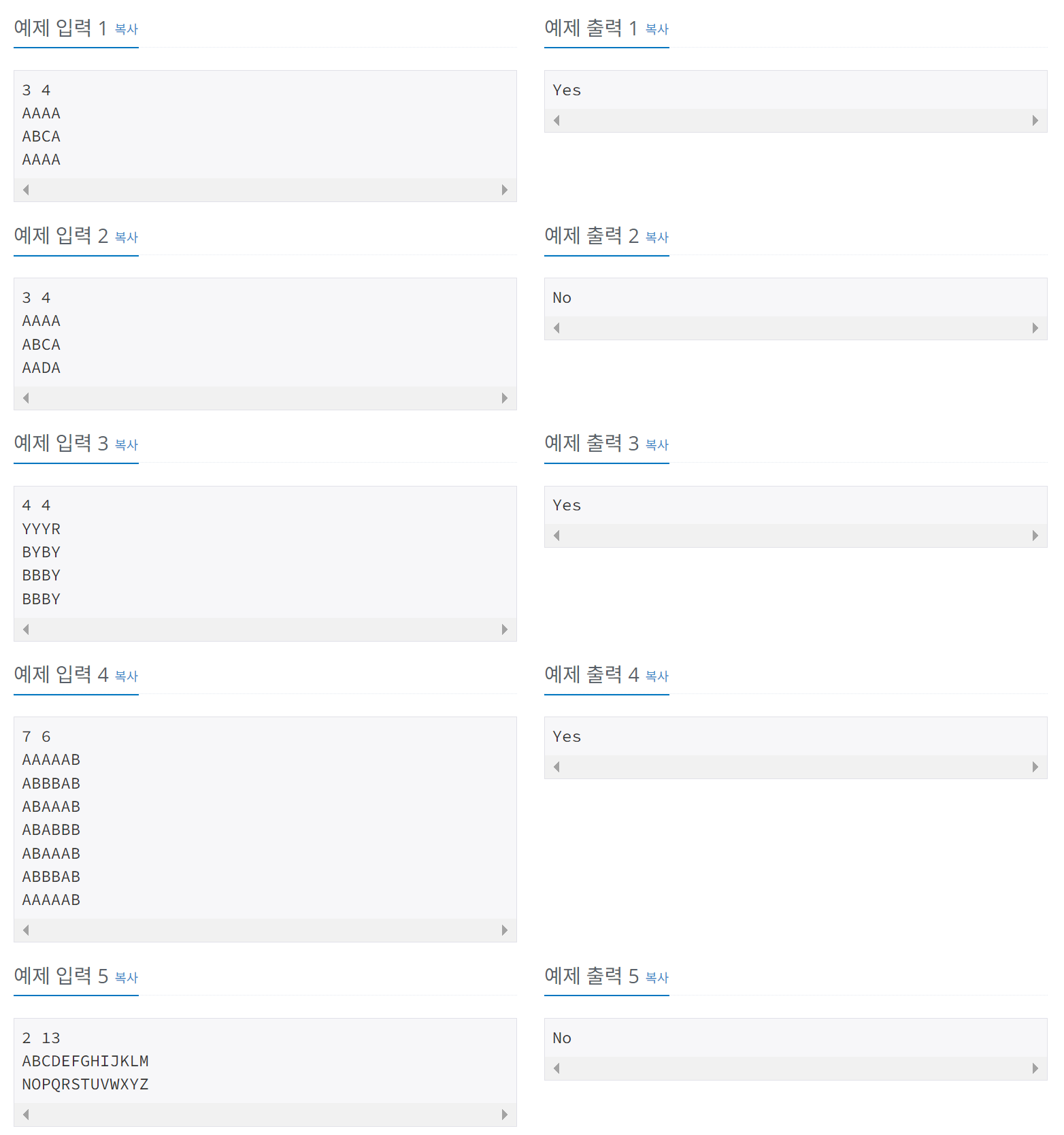
입력 & 출력 예시

🧑‍💻 코드

package Baekjoon;

import java.util.Scanner;

public class B_16929_TwoDots {
	static int n, m;
	static char[][] arr;
	static boolean[][] visited;
 	static int[] dx = {-1,1,0,0};
 	static int[] dy = {0,0,-1,1};
 	static boolean foundCycle;
 	
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		//입력
		n = sc.nextInt();
		m = sc.nextInt();
		arr = new char[n][m];
		visited = new boolean[n][m];
		
		for (int i = 0; i < n; i++) {
			String line = sc.next();
			for (int j = 0; j < m; j++) {
				arr[i][j] = line.charAt(j);
			}
		}
		
		//로직 
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < m; j++) {
				if(!visited[i][j]) dfs(i, j, -1, -1, 1);	
				if (foundCycle) break;
			}
		}
		
		//출력 
		System.out.println(foundCycle ? "Yes" : "No");
	}
	
	//fromX , fromY 부모 좌표  /  depth 현재까지 이동한 칸 수 
	private static void dfs(int x, int y, int fromX, int fromY, int depth) {
		visited[x][y] = true; //방문처리 
		
		for (int h = 0; h < 4; h++) {
			int nx = x + dx[h];
			int ny = y + dy[h];
			
			if (nx < 0 || nx >= n || ny < 0 || ny >= m) continue; //격자 범위 벗어나면 continue
			if (arr[x][y] != arr[nx][ny]) continue; //같은 알파벳이 아니면 continue
			if (nx == fromX && ny == fromY) continue; //바로 이전 칸으로 돌아가려는 경우 continue
			
			//방문처리 
			if (!visited[nx][ny]) {
				//같은 알파벳이고, 아직 방문하지 않았으면
				dfs(nx, ny, x, y, depth+1);
			} else {
				//이미 방문했고(visited==true), depth >= 4라면 사이클 발견
				// depth가 4 이상 일 때 사이클 인 이유는 사이클이 만들어지려면 최소 4개의 점이 필요하기 때문 
	            if (depth >= 4) {
	                foundCycle = true;
	                return;
	            }
			}
			
			if (foundCycle) break;
		}
		
	}

}

🔍코드해설

1️⃣ dfs(x, y, fromX, fromY, depth) - 사이클 탐지 DFS

// fromX, fromY : 바로 이전 좌표 / depth : 현재까지 이동한 칸 수
private static void dfs(int x, int y, int fromX, int fromY, int depth) {
    visited[x][y] = true; //방문처리 
    
    for (int h = 0; h < 4; h++) {
        int nx = x + dx[h];
        int ny = y + dy[h];
        
        if (nx < 0 || nx >= n || ny < 0 || ny >= m) continue; //격자 범위 벗어나면 continue
        if (arr[x][y] != arr[nx][ny]) continue; //같은 알파벳이 아니면 continue
        if (nx == fromX && ny == fromY) continue; //바로 이전 칸으로 돌아가려는 경우 continue
        
        if (!visited[nx][ny]) {
            //같은 알파벳이고, 아직 방문하지 않았으면
            dfs(nx, ny, x, y, depth+1);
        } else {
            //이미 방문했고(visited==true), depth >= 4라면 사이클 발견
            if (depth >= 4) {
                foundCycle = true;
                return;
            }
        }
        
        if (foundCycle) break;
    }
}

목적

현재 좌표 (x, y)에서 같은 알파벳을 따라 인접 칸을 탐색하며, 사이클(길이 ≥ 4) 이 존재하는지 판별
사이클을 발견하면 전역 플래그 foundCycle 을 true로 설정하고 탐색 종료

파라미터 설명

  • x, y : 현재 탐색 중인 좌표
  • fromX, fromY : 바로 이전(부모) 좌표 - 부모로 되돌아가는 경우를 판별하기 위해 필요
  • depth : 시작점에서 지금까지 이동해 온 칸 수 (시작 호출 시 1로 시작)

동작 흐름(한 단계씩)

  1. 현재 노드 방문 처리

    visited[x][y] = true;
    • visited[x][y] = true; 로 현재 칸을 방문 처리

  2. 상하좌우 4방향 반복

    • 각 방향에 대해 새 좌표 (nx, ny) 계산

  3. 범위 검사

    if (nx < 0 || nx >= n || ny < 0 || ny >= m) continue;
    • nx, ny가 격자 범위를 벗어나면 continue

  4. 같은 알파벳 검사

    if (arr[x][y] != arr[nx][ny]) continue;
    • arr[x][y] != arr[nx][ny] 으로 같은 알파벳이 아니면 그 방향은 탐색 대상 아님 → continue

  5. 부모(직전 칸) 검사

    if (nx == fromX && ny == fromY) continue;
    • nx == fromX && ny == fromY 인 경우는 바로 직전 칸(부모 칸)으로 되돌아가려는 동작이므로 무시 → continue

  6. 미방문이면 재귀 호출

    • !visited[nx][ny] 이면 dfs(nx, ny, x, y, depth+1) 로 깊이 증가시키며 재귀 탐색

  7. 이미 방문된 칸을 만난 경우(사이클 후보)

    • visited[nx][ny] == true 이면 그 칸은 이미 같은 연결 성분에서 방문된 칸

    • 이때 depth >= 4 라면 현재 경로가 최소 4칸 이상이며, 부모가 아닌 다른 방문 지점을 만난 것이므로 사이클로 판단

      • ⭐ depth가 4 이상 일 때 사이클 인 이유는 사이클이 만들어지려면 최소 4개의 점이 필요하기 때문

    • 사이클이면 foundCycle = true; 하고 return; (즉시 현재 DFS 흐름에서 탈출).

  8. 조기 종료 처리

    • 재귀 복귀 후에도 foundCycle 이 true이면 바깥 반복문을 멈추기 위해 break (또는 return) 처리

기저 조건

  • 명시적이지 않음
  • 이 DFS는 별도의 depth == something 같은 전형적 기저 조건이 없고,
    사이클 발견(visited 재방문 + depth >= 4) 이 사실상 종료 조건
  • 모든 분기에서 재귀가 끝나면 자연스럽게 반환되어 탐색 종료

왜 fromX/fromY가 필요한가?

  • DFS에서 인접한 부모 노드로 즉시 되돌아가는 것은 항상 발생하므로(바로 이전 좌표), 이것을 사이클으로 잘못 판단하지 않기 위해 부모 좌표를 비교하여 제외해야 함

구현 시 유의사항

  • ⭐ 사이클 판별 조건을 depth >= 4 로 두는 이유는 사이클은 최소 4개의 칸이 필요하기 때문

    • 두 칸이나 세 칸으로는 상하좌우 움직임 상 닫힌 사이클이 성립하지 않음

  • foundCycle 을 전역 플래그로 두면 재귀 깊게 내려간 상태에서도 빠르게 탐색을 멈출 수 있으므로 성능상 유리

    • foundCycle 이 true가 되면 가능한 한 빨리 return 하고 상위 호출들도 확인 후 종료
profile
Jimin Kwon
이전 포스트

[백준.G5] - 15686. 치킨 배달

다음 포스트

[백준.G5] - 2589. 보물섬

0개의 댓글