[머신러닝 인강] 6. 회귀분석(3)

수학적 개념이해 - 미분

미분의 개념

• 평균 변화율
  • $f(b)-f(a) \over {b-a}$

• 순간 변화율
  • $f^\prime(a) = \lim_{b\to{a}} {f(b)-f(a) \over {b-a}}$
  • 평균 변화율의 극한 값
  • b점이 a점으로 한없이 가까워질 때, a점에서의 순간변화율
  • a점에서의 접선의 기울기

• 다항함수 미분 및 미분 기본 공식
  • $f(x) = c \Rightarrow f^\prime(x) = 0$, $c$는 상수
  • $f(x) = x^n \Rightarrow f^\prime(x) = nx^{n-1}$, $n$은 자연수
  • (참고) $f(x) = x^k \Rightarrow f^\prime(x) = kx^{k-1}$, $k$sms 유리수
  • $\{cf(x)\}^\prime = cf^\prime(x)$
  • $\{f(x)\pm g(x)\}^\prime = f^\prime(x) \pm g^\prime(x)$

• 곱의 미분
  • $\{f(x)g(x)\}^\prime = f^\prime(x)g(x) + f(x)g^\prime(x)$

• 합성함수 미분
  • $f(g(x))^\prime = f^\prime(g(x))g^\prime(x)$

• 지수함수 미분
  • $\{e^x\}^\prime = e^x$
  • $\{a^x\}^\prime = a^xlna$

• 로그함수 미분
  • $\{lnx\}^\prime = {1 \over x}$
  • $\{log_ax\}^\prime = {1 \over xlna}$

미분의 활용

• 극댓값, 극솟값
  • 도함수를 통하여 미분가능한 함수의 극댓값, 극솟값을 구할 수 있음

Likelihood

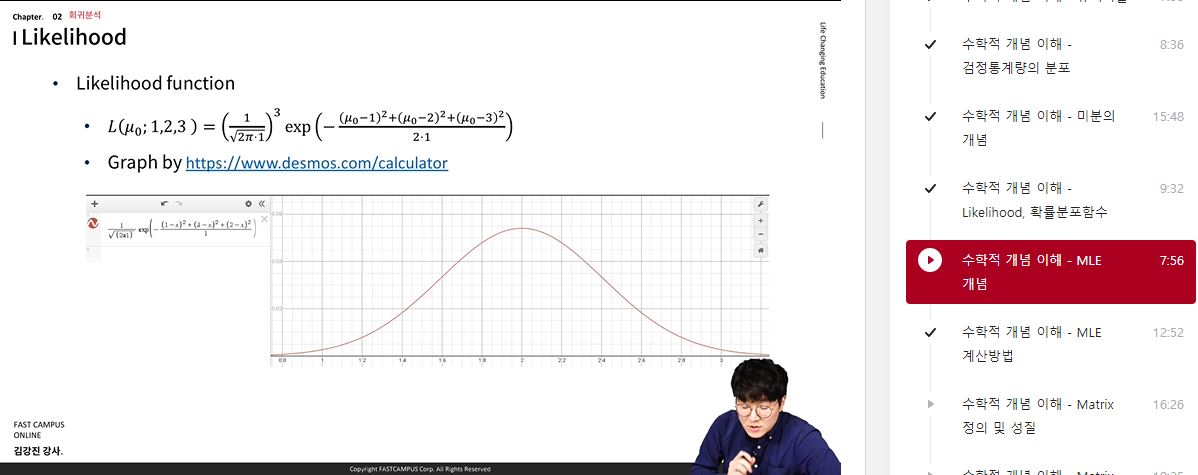
• Likelihood function (가능도함수/우도함수)
  • 모평균이 $\mu_0$일 때 표본$x$가 얻어질 확률
  • 가능도함수를 최대로 만드는 $\hat{\mu_0}$를 모평균으로 추정

• 확률분포함수(Probability distribution function)
  • 모수를 알 때, 확률변수의 실현값을 예측하고자 함
  • 종류
    • 확률밀도함수(Probability density function) - 연속형 확률변수의 확률 분포함수
    • 확률질량함수(probability mass function) - 이산형 확률변수의 확률 분포함수
      • $f(x) = P(X=x)$
    • 누적분포함수(Cumulative distribution function) - 누적 확률 분포함수
      • $F(x) = P(X\le x)$

• 가능도함수(Likelihood function)
  • 확률변수의 실현값을 알 때(데이터가 있을 때), 모수를 추정하고자 함

• Probability density function
  • 평균$\mu_0$, 분산1을 독립 정규분포를 따르는 확률변수 $X_i$의 확률분포함수(확률밀도함수)
    • $f(x_i) = \left( {1 \over\sqrt{2\pi\cdot1}}\right)\exp\left(-{(x_i-\mu_0)^2 \over 2\cdot1}\right)$
  • $X_1 = x_1, X_2 = x_2, X_3 = x_3$, 3개의 자료가 있을 때, 확률분포함수
    • $f(x_1,x_2,x_3) = \left( {1 \over\sqrt{2\pi\cdot1}}\right)^3\exp\left(-{(x_1-\mu_0)^2 + (x_2-\mu_0)^2 + (x_3-\mu_0)^2 \over 2\cdot1}\right)$

• Likelihood function
  • 동일한 함수이나, $\mu_0$를 변수로 인식
    • $L(\mu_0;x_1,x_2,x_3) = \left( {1 \over\sqrt{2\pi\cdot1}}\right)^3\exp\left(-{(\mu_0-x_1)^2 + (\mu_0-x_2)^2 + (\mu_0-x_3)^2 \over 2\cdot1}\right)$
  • $X_1 = 1, X_2 = 2, X_3 = 3$일 때,
    • $L(\mu_0;1,2,3) = \left( {1 \over\sqrt{2\pi\cdot1}}\right)^3\exp\left(-{(\mu_0-1)^2 + (\mu_0-2)^2 + (\mu_0-3)^2 \over 2\cdot1}\right)$$

• Maximum Likelihood Estimator(MLE)
  • 정의: Likelihood를 최대롤 만드는 모수의 값
  • 주로 모수에 hat을 붙여 $(\hat\mu)$표현
  • Likelihood는 $\mu_0$에 대한 함수
    • $\hat\mu=$ 최댓값을 가지는, 극댓값을 가지는, Likelihood를 $\mu_0$로 미분해서 0을 만드는 값

미분의 활용 - MLE

• $\mu_0$ MLE 구하기
  • Likelihood 구성
    • $L(\mu;1,2,3) = \left( {1 \over\sqrt{2\pi\cdot1}}\right)^3\exp\left(-{(\mu_0-1)^2 + (\mu_0-2)^2 + (\mu_0-3)^2 \over 2\cdot1}\right)$
  • 미분하기 용이하도록 log Likelihood 구성
    • $logL(\mu_0;1,2,3)=-{3 \over 2}log(2\pi)-{1 \over2}\left((\mu_0-1)^2 + (\mu_0-2)^2 + (\mu_0-3)^2\right)$
  • 미분 실행
    • ${\delta logL(\mu_0;1,2,3) \over\delta\mu_0} = -{1 \over2}(2(\mu_0-1) + 2(\mu_0-2) + 2(\mu_0-3))$
  • 미분한 함수가 0이 되게 하는 $\hat{\mu_0}$를 구해냄
    • $-{1 \over2}(2(\hat{\mu_0}-1) + 2(\hat{\mu_0}-2) + 2(\hat{\mu_0}-3)) = 0$
    • $3\hat{\mu_0} = 1+2+3$
    • $\hat{\mu_0} = 2$

• $\sigma^2$ MLE 구하기
  • Likelihood 구성, $\lambda = \sigma^2$
    • $L(\mu;1,2,3) = \left( {1 \over\sqrt{2\pi\cdot\lambda}}\right)^3\exp\left(-{(\mu_0-1)^2 + (\mu_0-2)^2 + (\mu_0-3)^2 \over 2\cdot\lambda}\right)$
  • 미분하기 용이하도록 log Likelihood 구성
    • $logL(\mu_0;1,2,3)=-{3 \over 2}log(2\pi\lambda)-{1 \over2\lambda}\left((\mu_0-1)^2 + (\mu_0-2)^2 + (\mu_0-3)^2\right)$
  • 미분 실행
    • ${\delta logL(\mu_0;1,2,3) \over\delta\lambda} = -{3\over2}\cdot{1\over\lambda}+{1 \over2}(\lambda)^{-2}((\mu_0-1)^2 + (\mu_0-2)^2 + (\mu_0-3)^2)$
  • 미분한 함수가 0이 되게 하는 $\hat\lambda$를 구해냄
    • $-{3\over2}\cdot\hat\lambda+{1\over2}((\mu_0-1)^2 + (\mu_0-2)^2 + (\mu_0-3)^2) = 0$
    • $\hat\lambda = {1\over3}((\mu_0-1)^2 + (\mu_0-2)^2 + (\mu_0-3)^2)$

머신러닝과 데이터 분석 A-Z 올인원 패키지 Online. 👉 https://bit.ly/3cB3C8y