Problems
백준 문제풀이
동전 0
잃어버린 괄호
이항 계수 1
ATM
최소공배수
영화감독 숌
터렛
Attempts
동전 0
K원을 만드는데 필요한 동전 개수의 최솟값
동전들이 배수 관계라서 Greedy로 풀 수 있다. (배수 아니면 Greedy로는 못 품).
처음에는 전체 동전 배열과 사용 가능한 동전 배열을 분리해서 고민했었는데, 그냥 전체 동전 배열을 루프하면서 조건을 설정하면 된다.
for (int i = N-1; i >=0 ; i--) {
if(K >= coin[i]){ // 사용 가능한 동전 조건
count += K/coin[i];
K = K % coin[i];
}
}잃어버린 괄호
괄호를 적절히 쳐서 식의 값을 최소로 만들기
어떻게 +,-를 나눌지 고민하다가 페어의 의견을 바탕으로 먼저 -를 delimiter로 하여 split 함. 이렇게 나누면 첫번째 원소만 양수인 상황이 되므로 첫번째 원소만 sum += 하였고 나머지는 sum -= 하였다.
String str = br.readLine();
String[] str_arr = str.split("-");
int sum = 0;
for(int i=0; i < str_arr.length;i++){
String[] plus = str_arr[i].split("\\+");
for(int j =0; j < plus.length;j++){
if(i==0){//
sum += Integer.parseInt(plus[j]);
}
else
sum -= Integer.parseInt(plus[j]);
}
}한편 +를 delimiter로 하고 싶을 때는 split("\\+") 처럼 \\가 필요하다
이항 계수 1
이항 계수 를 구하라
Combination 구하는 식과 같으므로 팩토리얼이 필요하다.
팩토리얼 구하는 메서드의 경우 페어의 의견을 바탕으로 재귀로 구현.
//main 메서드 밖에서 static 메서드로 정의한 경우
//객체 생성하지 않아도 접근 가능함
static int fac(int n){
if(n <= 1){
return 1;
}
else{
return fac(n-1) * n ;
}
}메서드를 작성할 때 static이 아닌 경우들도 시도를 해 보았다.
- (백준 제출용)Main 클래스 안, main 메서드 밖에서 static이 아닌 메서드를 정의해봄. 재귀할 때
this.메서드이름()으로 해야 하는듯
//main 메서드 안에서
//Main objName = new Main()으로 객체 생성 후
//objName.fac()으로 접근
int fac(int n){
if(n <= 1){
return 1;
}
else{
return this.fac(n-1) * n ;
}// this가 없으니 오류나더라
}- Main 클래스 안, main 메서드 밖에서
static class생성 후 메서드 정의해봄.static이 아닌 클래스는 안 되는것 같음
//main 메서드 안에서
//FacClass objName = new FacClass()로 객체 생성 후
//objName.fac()으로 접근
static class FacClass{
//생략
}- Main 클래스 밖에서
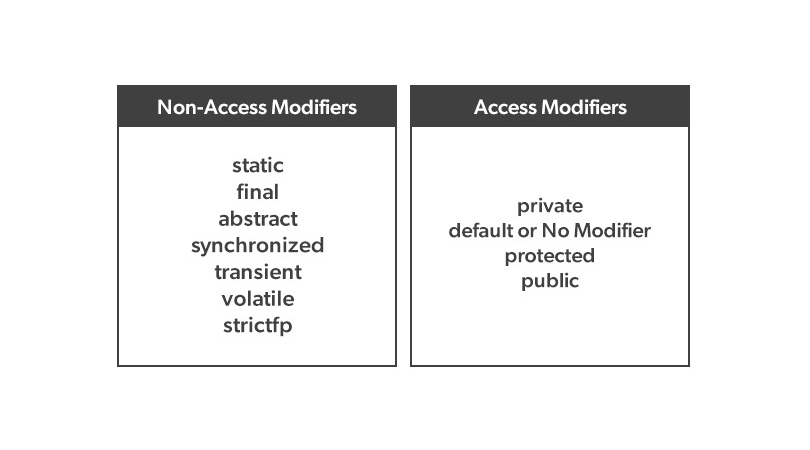
class생성 후 메서드 정의해봄. 이 경우 default(package-private)가 적용되는것 같음.In Java, there are four access levels:
public,protected,private, and default (also known as package-private).
The default access allows the class, variable, or method to be accessed within the same package but not from other packages.
//main 메서드 안에서
//FacClass objName = new FacClass()로 객체 생성 후
//objName.fac()으로 접근
class FacClass {
//생략
}한편 static은 non-access modifier로, public과 같은 access modifier는 아니다.
ATM
각 사람이 돈을 인출하는데 필요한 시간의 합의 최솟값
시간의 합을 최소로 하기 위해 오름차순으로 정렬 후 을 구현해 준다.
Arrays.sort(arr);
int sum = 0;
for(int i = 0; i<N;i++){
for(int j = 0; j<=i; j++){
sum += arr[j];
}
}최소공배수
이전에 최대공약수를 구하는 알고리즘을 올린 적이 있다. 그리고 최소공배수는 두 수를 곱하고 최대공약수로 나눈 것과 같다.
이곳에서 증명을 볼 수 있다.
int gcd = 1;
for(int j = 1; j<=a && j<=b; j++){
if(a%j==0 && b%j==0)
gcd = j;
}
int lcm = a*b/gcd;영화감독 숌
어떤 수에 6이 적어도 3개 이상 연속으로 들어가는 수
6이 3개 이상 연속으로 들어간 수 중에서 N번째 수를 찾아야 한다.
처음에는 규칙성을 찾으려고 노력했으나... 찾을 수 없었다. 멘토님 의견을 바탕으로 브루트포스를 사용하기로 함.
N번째를 찾을 때까지 모든 자연수에 대해 문자열로 바꾸었을 때 "666"을 포함하는지 검사한다.
// checkEveryNum은 666이 최소이기 때문에 666부터 검사해도 된다.
while(count != N){
if(String.valueOf(checkEveryNum).contains("666"))
count ++;
checkEveryNum++;
}터렛
목표가 위치할 수 있는 좌표의 수를 출력
두 원의 반지름과 중심간 거리의 관계를 고민했는데, 한 원이 다른 원 내부에 있는 경우를 제대로 고려하지 못하여 굉장히 헤멤.
// distance = 두 원의 중심 간의 거리
// a[2]와 b[2]는 각 원의 반지름임
if (distance == 0) {
if (a[2] == b[2])
// Circles coincide
sb.append("-1\n");
else
// One circle is inside the other
sb.append("0\n");
}
else {
if (distance > a[2] + b[2] || distance < Math.abs(a[2] - b[2]))
// Circles do not intersect
sb.append("0\n");
else if (distance == a[2] + b[2] || distance == Math.abs(a[2] - b[2]))
// Circles are tangent to each other
sb.append("1\n");
else
// Circles intersect at two points
sb.append("2\n");
}Results
워밍업 알고리즘 문제 목록에서 아직 동적계획법은 손대지 못함.
Insights
앞서 다룬 스택과 큐에 이어 Greedy, Brute Force, Number Theory and Combinatorics 입문 문제들을 풀어보면서 프로그래밍을 하는데 있어 적절한 알고리즘과 적절한 자료구조의 중요성을 체감하게 되었다.