Fibonacci Number
문제
https://leetcode.com/problems/fibonacci-number
풀이
단순히 0~30까지의 피보나치 수를 구하는 문제이다.
피보나치 수를 풀 때는 "재귀"와 "DP"로 풀 수 있다.
두 가지 방법으로 풀어보자!
재귀
재귀(Recursion)는 어떤 문제를 해결하기 위해 자기 자신을 다시 호출하는 방법이다.
fib(n) = fib(n-1) + fib(n-2) 처럼 자기 자신(fib)를 계속 호출하는 공식과 잘 어울리는 방법이다.
우리는 fib라는 함수를 잘 정의해놓으면 계속해서 fib라는 함수만 호출해서 피보나치 수를 정의할 수 있다.
class Solution {
public int fib(int n) {
if(n == 0) return 0;
if(n == 1) return 1;
return fib(n-1) + fib(n-2);
}
}18ms
하지만 재귀 함수는 좋지 않은 성능을 보일 수 밖에 없다.
예를 들어 4번째 피보나치 수를 구하는 과정을 살펴보자.
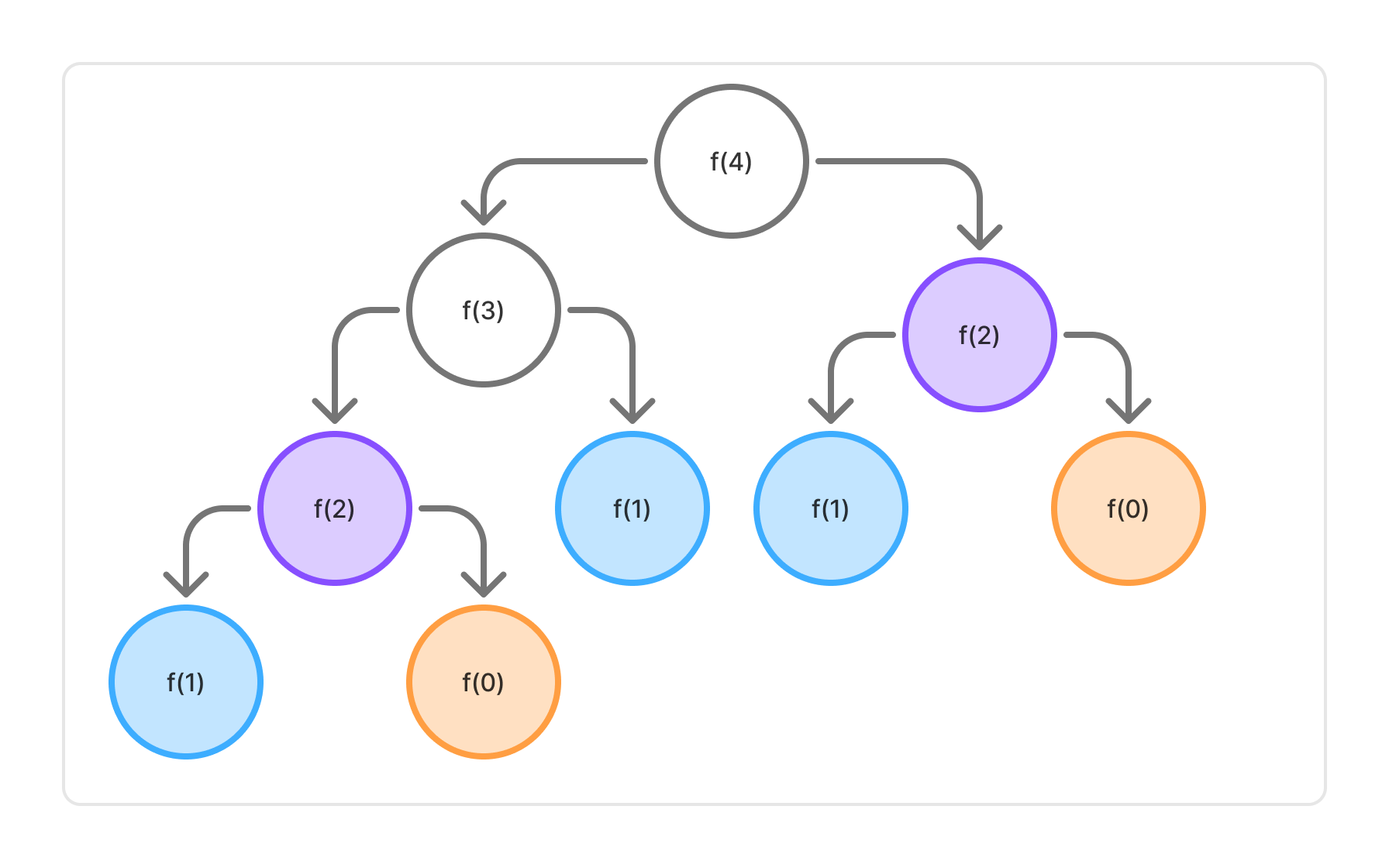
다음과 같이 fib(4)를 구하기 위해서 fib(3)과 fib(2)를 확인하는데,
fib(3)을 구하는 과정에서 또 fib(2)를 확인하는 과정이 있다.
즉, 확인해야 하는 범위가 계속해서 겹치지만 또 다시 연산을 하고 있다.
만약 fib(30)이라는 최대 값을 넣게 된다면 겹치는 범위도 상당히 많을 것이고, 불필요한 연산도 굉장히 늘어나게 될 것이다.
따라서 우리는 "DP"라는 방식을 사용할 것이다.
DP
DP는 "Dynamic Programming"의 약자로 동적 계획법이라고도 불린다.
복잡한 문제를 더 작은 하위 문제로 나누어 해결하는 알고리즘 설계 기법이다.
즉, fib(4)를 구할 때 더 작은 하위 문제인 f(3),f(2)를 먼저 해결하고 그 결과를 통해 복잡한 문제를 풀겠다는 것이다.
따라서 다음과 같이 하위 문제들을 미리 해결하고 배열에 값을 저장해놓는다.
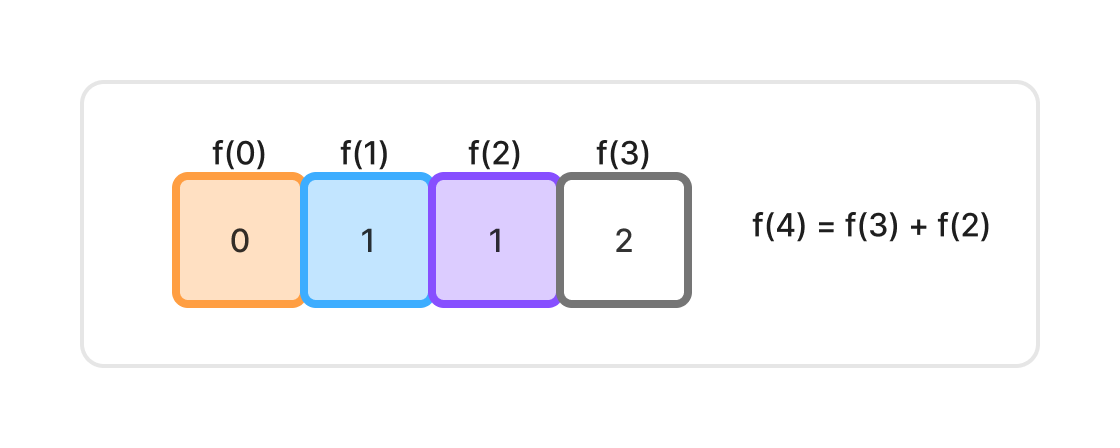
그리고 마지막 복잡한 문제인 fib(4)를 해결할 때는
이미 해결해놓은 f(3)과 f(2)의 값을 가져오기만 하면 된다.
class Solution {
public int fib(int n) {
if (n==0) return 0;
if (n==1) return 1;
int [] arr = new int[n+1];
arr[0] = 0;
arr[1] = 1;
for (int i=2; i<=n; i++) {
arr[i] = arr[i-1] + arr[i-2];
}
return arr[n];
}
}0ms
재귀처럼 이미 해결된 문제를 다시 해결할 필요가 없이
결과값만 가져오면 되므로 훨~씬 빠르게 작동하였다!
👏👏

