[CS] 시간 복잡도

시간 복잡도(Time Complexity)는 알고리즘의 성능을 평가하기 위한 중요한 지표로, 입력 크기와 실행 시간 간의 관계를 나타냅니다. 프로그램이 실행되는 데 걸리는 시간을 이론적으로 분석하여 성능을 비교하고 최적화할 수 있도록 돕습니다.

1. 시간 복잡도의 정의

시간 복잡도는 알고리즘이 특정 입력 크기에서 얼마나 많은 연산을 수행하는지를 나타냅니다. 이를 통해 입력 크기가 커질수록 알고리즘이 얼마나 효율적으로 동작하는지 평가할 수 있습니다.

2. 시간 복잡도의 표기법: Big-O 표기법

Big-O 표기법은 시간 복잡도를 수학적으로 나타내는 표기법입니다. 알고리즘의 성능을 표현할 때 가장 최악의 경우를 기준으로 계산합니다.

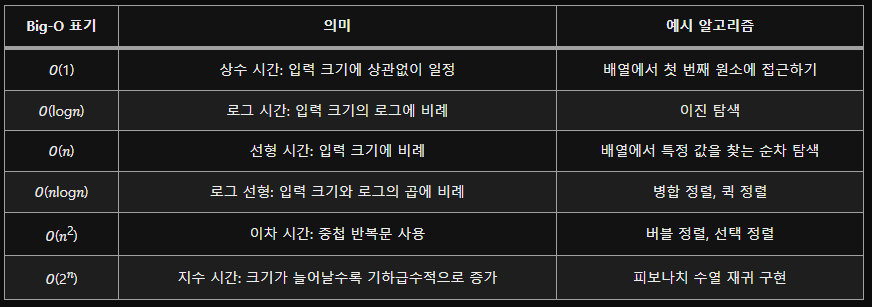
Big-O 표기	의미	예시 알고리즘
𝑂(1)	상수 시간: 입력 크기에 상관없이 일정	배열에서 첫 번째 원소에 접근하기
𝑂(log⁡𝑛)	로그 시간: 입력 크기의 로그에 비례	이진 탐색
𝑂(𝑛)	선형 시간: 입력 크기에 비례	배열에서 특정 값을 찾는 순차 탐색
𝑂(𝑛log⁡𝑛)	로그 선형: 입력 크기와 로그의 곱에 비례	병합 정렬, 퀵 정렬
𝑂(𝑛2)	이차 시간: 중첩 반복문 사용	버블 정렬, 선택 정렬
𝑂(2𝑛)	지수 시간: 크기가 늘어날수록 기하급수적으로 증가	피보나치 수열 재귀 구현

3. 시간 복잡도 계산 방법

1) 반복문

다음 코드에서 시간 복잡도를 분석해 보겠습니다.

// 배열의 합 계산
int sum = 0;
for (int i = 0; i < n; i++) {
    sum += array[i];
}

• 반복문이 입력 크기 𝑛만큼 실행되므로, 시간 복잡도는 O(n)입니다.

2) 중첩 반복문

// 2중 반복문
for (int i = 0; i < n; i++) {
    for (int j = 0; j < n; j++) {
        System.out.println(i + ", " + j);
    }
}

• 내부 반복문이 외부 반복문마다 𝑛번 실행되므로, 총 n×n=n^2번 연산합니다. 시간 복잡도는 O(n^2)입니다.

4. 시간 복잡도의 실제 활용

1) 알고리즘 선택

• 정렬 문제: 데이터가 많을수록 O(nlogn) 이상의 알고리즘을 사용하는 것이 유리합니다.
• 탐색 문제: 이진 탐색과 같은 O(logn) 알고리즘을 사용하면 효율적입니다.

2) 성능 최적화

알고리즘을 작성할 때 시간 복잡도를 줄이기 위한 코드를 작성해야 합니다. 예를 들어, 반복문을 줄이거나 동적 프로그래밍(DP)을 활용하면 효율성을 크게 향상시킬 수 있습니다.

5. 시간 복잡도의 실제 비교 예시

선형 탐색 vs 이진 탐색 비교

알고리즘	시간 복잡도	입력 크기 (n)	최대 연산 횟수
선형 탐색	𝑂(𝑛)	1,000,000	1,000,000 번
이진 탐색	𝑂(log⁡𝑛)	1,000,000	20 번

6. 주의점: 시간 복잡도의 한계

• 실제 실행 시간과 차이: 이론적인 시간 복잡도가 낮더라도 구현이나 환경에 따라 실행 시간이 더 걸릴 수 있습니다.
• 메모리 복잡도와의 균형: 시간 복잡도를 줄이는 대신 메모리를 더 많이 사용할 수도 있습니다.