[NLP] Beam search

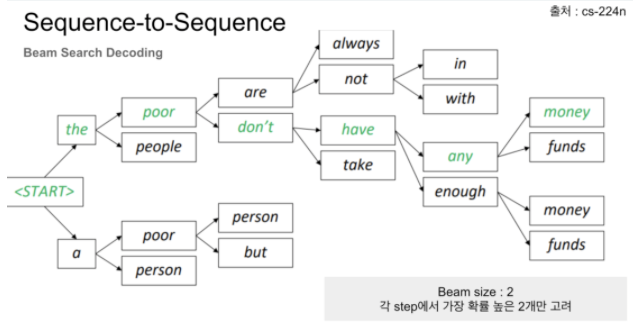
자연어 생성 모델에서 테스트 시점에 보다 좋은 품질을 얻을 수 있게 해주는 알고리즘인 Beam search를 알아보자.

Greedy decoding

앞서 배운 seq2seq와 같은 모델에서 단어를 생성할때 현재 time step에서 가장 확률이 높은것을 채택하는 방법을 Greedy decoding이라고 한다.

"Greedy decoding has no way to undo decisions"이 문장처럼 결정을 되돌릴 방법이 없다는게 큰 단점이다. 단어를 앞부분에서 잘못 생성되면 그 후부터는 계속 잘못된 문장이 생성될 수 있다.

Exhaustive search

joint probability

매순간 마다 가능한 모든 경우의 수를 찾아보는 방법도 존재하는데 이 경우 $V^t \,\,(V=사전사이즈)$라는 굉장히 많은 탐색을 요구하게 된다.

Beam search

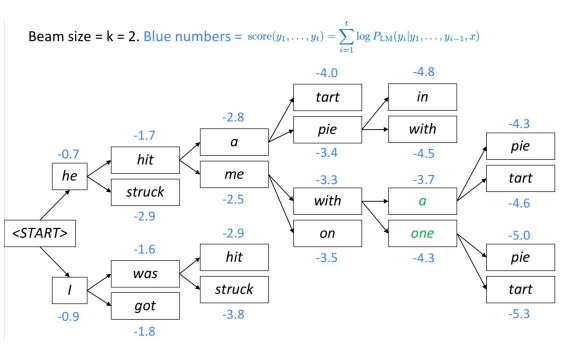
따라서 우리는 Greedy(한가지만 고려)와 Exhaustive(전체를 고려)의 중간쯤에 있는 접근법을 생각하게 되는데 그게 Beam search이다.

이 알고리즘의 핵심 아이디어는 decoder의 매 time step마다 우리가 정하는 파라미터(beam size) $k$개를 고려하고 최종적으로 $k$개 중 가장 확률이 높은 선택을 하게 된다.

일반적으로 $k$는 5에서 10사이의 값을 사용한다.

확률값을 곱하는 형태로도 수식을 전개할 수 있지만 $log$의 성질을 사용하여 확률 값을 더하게끔 유도한다. $log$는 단조 증가함수이기 때문에 $log$를 취한값도 그 상태로 유지되기 때문에 가능하다.

Greedy decoding의 경우 <end>토큰이 나오는 시점에서 생성이 중단되지만 beam search의 경우 각 hypotheses(k개의 생성문장)마다 다른 시점에 <end>토큰이 생성된다.

• 한 hypothesis에서 <end>가 발생했다면 끝났다고 가정하여 따로 저장을 한다.

• 나머지 hypoheses도 <end>가 발생할때까지 beam search를 수행하는 과정을 반복한다.

• beam search의 최종 종료는 우리가 정해둔 임의의 time step $T$에 도달하면 멈추거나 따로 저장해둔 가설들의 개수가 $n$개에 도달하면 종료하는 방법을 사용한다.

완성된 가설들의 리스트들 중 가장 높은 score를 가지는 하나의 후보를 뽑아야 한다. 이 후보를 선택하는 기준은 $log$확률 값을 사용하게 되는데 sequence의 길이가 긴 가설일수록 더 많은 음의 값이 더해지기 때문에 $log$확률은 낮은 값을 가질것이다.

따라서 공평한 비교를 위해 Normalize by length를 부여하게 된다.