Important Concepts in Optimization
-
Generalization
-
Under-fitting vs. over-fitting
-
Cross validation
-
Bias-variance tradeoff
-
Bootstrapping
-
Bagging and boosting
Generalization
-
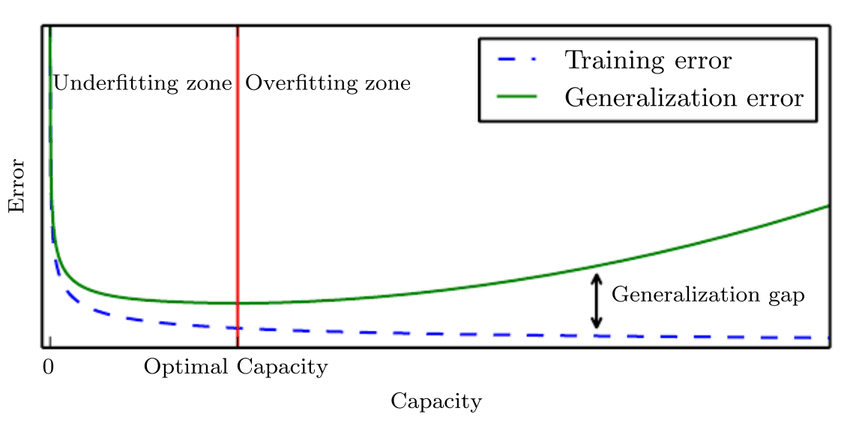
일반적으로 Training error는 줄어들지만 이 지표만으로 성능이 좋다고 할 수 없다.
-
Generalization gap이란 것은 Training error와 Test error와의 차이를 의미한다.
-
Generalization perfomance는 학습데이터와 테스트데이터 사이의 차이를 일반화하는 것이기 때문에 모델의 직접적인 성능이 좋은 것은 아니다.
Underfitting vs. Overfitting
-
Overfitting은 학습데이터에는 잘 동작하지만 테스트데이터에는 그렇지 않는 상황
-
Underfitting은 네트워크가 너무 간단하거나 학습을 조금 하는 경우 학습데이터 조차 잘 맞추지 못하는 상황
Cross-validation
-
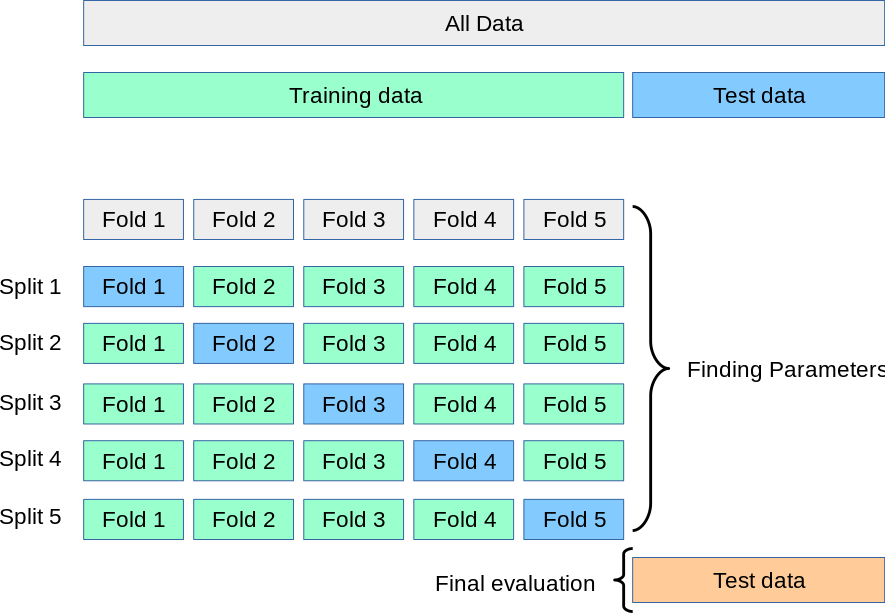
일반적으로 학습데이터와 테스트데이터를 나눠서 사용한다.
-
그렇다면 학습데이터와 테스트(검증)데이터를 얼마만큼 나눠야 할까?
-
위의 의문에 대한 방법론이 Cross-validation이다.
Bias and Variance
-
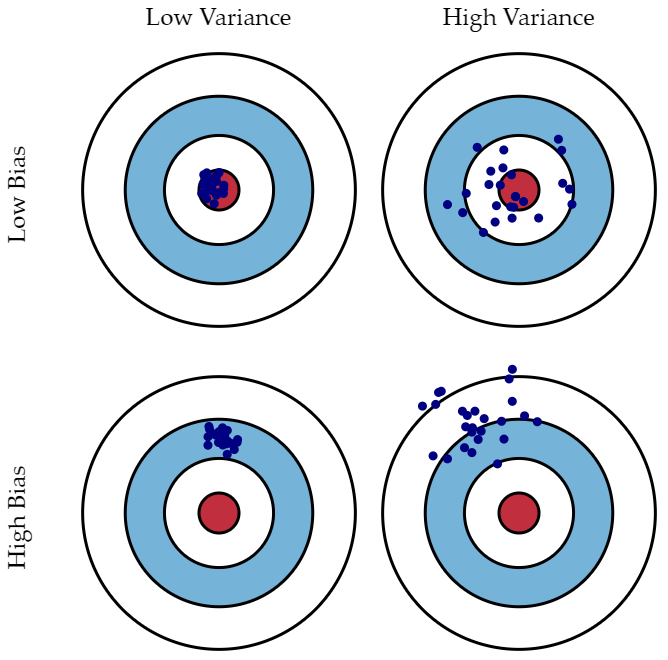
variance는 어떤 입력에 대하여 출력이 얼마나 일관적인가의 척도이다.
-
Low variance는 출력이 일관적이고, High variance는 출력이 많이 달라지는 것을 의미한다.
-
bias 평균적으로 Target에 가까운 척도이다.
-
Low bias는 출력들이 Target에 가까우며 High bias는 Target 거리가 먼 경우를 의미한다.
Bias and Variance Tradeoff
- bias가 줄어들면 variance가 증가할 수 밖으며 그 반대도 마찬가지인 경우
Bootstrapping
- 학습데이터 전체가 아닌 일부(sub-sampling)를 사용해 여러가지 모델 또는 메트릭을 만들어 이 결과값들을 활용하는 경우
Bagging vs. Boosting
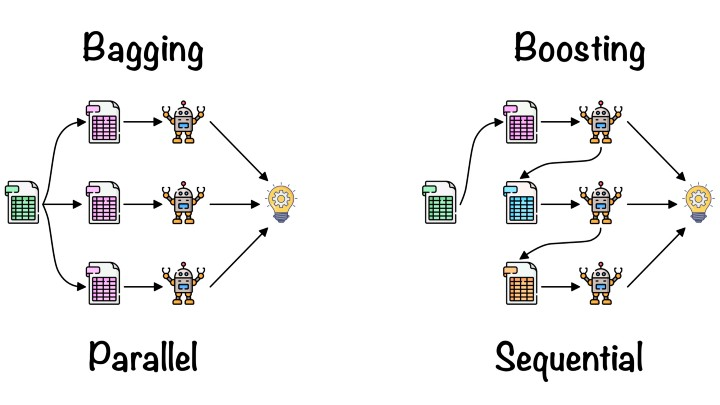
- Bagging (Bootstrapping aggregating)
- 학습데이터가 고정 된 경우 다 활용해 한 개의 모델을 만드는 것이 아니라 sub-sampling을 통한 여러개의 데이터를 활용해 여러 모델의 결과값의 평균을 보는 경우
- Boosting
- 간단한 모델을 만들어 학습 데이터에 대해 예측해보고 잘 예측 못한 데이터에 대해서만 잘 동작하는 모델을 만들어 sequencial하게 모델들을 합쳐 하나의 모델을 만드는 경우
Gradient Descent Methods
-
Stochastic gradient descent
- 한 번에 하나의 샘플에 대해 gradient를 구해 업데이트를 하는 방법
-
Mini-batch gradient descent
- 전체도 아니고 한개도 아닌 일반적으로 사용하는 batch(64, 128..)로 gradient를 구해 업데이트를 하는 방법
-
batch gradient descent
- 전체의 데이터를 사용해 업데이트를 하는 방법
-
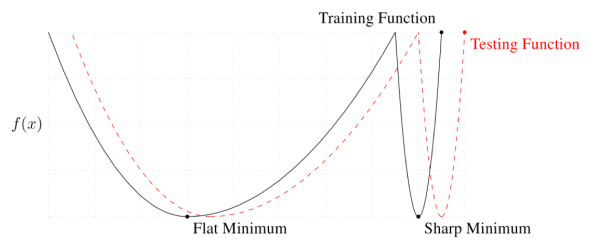
batch size가 클 경우 sharp minimum에 도달하고 batch size가 작을 경우 flat minimun에 도달한다.
-
위 그림을 예시로 빨간색 점선이 우리가 원하는 목적함수라 할 때, Flat minimum은 실제 목적함수와 거리가 있어도 작은 값을 나타내지만 sharp minimum은 약간의 차이가 매우 큰 값을 나타낼 수 있기 때문에 batch size를 작게하여 flat minimum에 도달하는 것을 권장한다.
Gradient Descent
: Learning Rate
: Gradient
문제점
-
적절한 learning rate를 구하기 매우 힘듬
-
이 문제점을 개선하고자 한 방법이 optimizer이다.
Momentum
: accumulation
: momentum parameter
-
기본 업데이트는 해당 time의 값만 사용하여 업데이트를 하게 된다.
-
momentum term을 이용해 이 전 batch에서의 흐름을 활용해 사용한다.
Nesterov Accelerated Gradient
-
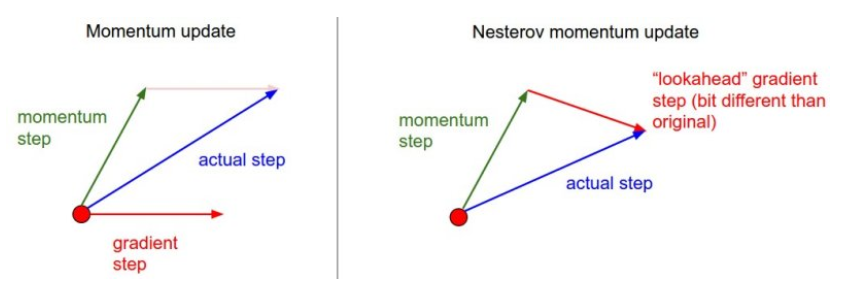
Momentum과의 차이점은 값을 구할 때 다음 위치로 이동해보고 거기서의 gradient를 계산한 것을 사용해 구하는 차이점이 있다.
-
momentum을 관성이라고 이해한다면 local minima로 수렴하는데 걸리는 시간이 오래걸리지만 NAG는 그 다음 위치에서의 기울기를 활용하기 때문에 조금 더 빠르게 최소값을 찾을 수 있다.
Adagrad
: sum of gradient squares
: for numerical stability
-
Adapts the learning rate로 이전 까지 파라미터들이 얼마나 변했는지를 통해 작게 변한 파라미터는 크게 변화 시키고 크게 변화한 파라미터는 작게 변화시키고 싶은 아이디어
-
그 동안 얼마나 변해왔는지 저장해두는 값이 이다.
-
값은 기울기를 제곱한 값들의 합이기 때문에 이 값을 역수로 취하면 크게 변한 파라미터들은 작게, 작게 변한애들은 크게 변화시킬 수 있다.
-
가장 큰 문제점은 가 계속 커지기 때문에 위 수식이 0에 수렴할 수 있기 때문에 뒤로 갈수록 학습이 안될 수 있다.
Adadelta
-
가 계속 커지는 것을 막으려는 것이 초점이다.
-
Adadelta는 learning rate가 없기 때문에 활용이 잘 되지는 않는다.
RMSprop
- learning rate가 들어간 점이 차이점이다.
Adam
: Momentum
: EMA of gradient squares
- 모멘텀까지 활용한 optimization