막 쓰는 선형대수 1

모든 자료는 이곳에서 출처를 둠

선형대수는 선형방적식을 풀기 위한 방법론
2x + 3y = 0 과 같은 방정식이 있을 때, 이 식을 만족하는 x, y를 찾는 것이 목표이다.
미지수가 1개이고 방정식이 1개가 주어졌을 때는 쉽게 다가갈 수 있다.

$2x + 1 = 5$

$x = 2$

하지만 미지수가 두개이고 방정식이 1개만 주어졌을 때는 찾아내기 힘들다.
$2x + 3y = 0$

직관 or 값을 대입해보며 문제를 해결해야 한다.
미지수가 2개일 때 방정식이 2개 주어진다면?

$2x + 3y = 0\\ x + y = 5\\ x = 15 , y = -10로 접근 가능함$

이 처럼 방정식의 관계를 이용하여 문제를 해결하기 위한 방법중 하나가 선형대수이다.

• 선형

$f(ax) = af(x)$
$f(x+z) = f(x)+f(z)$

선형이다 라는 것은 입력값 x에 어떤 값을 넣어도 a만큼의 영향을 받고 그 결과 또한 a만큼의 영향을 받아서 나오는 것을 의미한다.

$y=2x일때, x=5 이면 y=10이다.$
$2(y=x)일때, x=5이면, 그 결과가 10이다.$

즉 입력값에 2배의 영향을 주면 결과값 y도 2배의 영향을 받는 것

$y=2(x+z)일때, x=2, z=3이면\\ y=2(2+3)\\ =2(2) + 2(3)\\ =10$
으로 나타낼 수 있다.
이와 같은 특징을 선형성을 같는다라고 한다.

• 대수 : 숫자를 대신하다. ( 방정식의 미지수 x,z ... )
• 선형대수 : 선형적 특징을 가지는 숫자를 대신하는 것으로 이루어진 방정식의 접근법

$2x -y = 0\\ -x + 2y = 3$

이라는 방정식들은 행렬로 표현을 할 수 있음 ( 계수 행렬, 미지수 벡터, 우변 벡터 )

$\begin{bmatrix} 2 & -1\\ -1 & 2 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}= \begin{bmatrix} 0 \\ 3 \end{bmatrix}$

<계수행렬><미지수벡터> = <우변 벡터>로 이루어져 있다.

위의 시스템에서 알아야 하는 3가지 정보에 대해서 알아보자.

1. Row picture
하나의 row방향의 방정식을 따져 보는 것.
$y=2x$
$y=\frac{x}{2}+\frac{3}{2}$

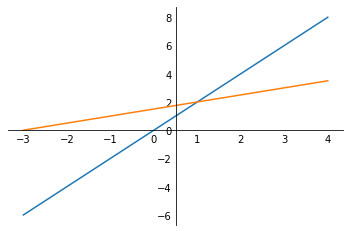
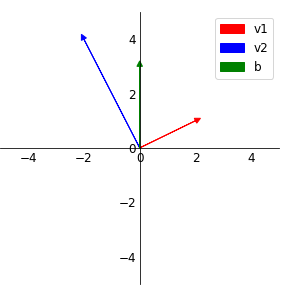
(1,2)에 교점이 생기는 것을 볼 수 있다.
선형대수의 행렬에서 row picture는 row방향 방정식들을 나타내고 이런 방정식들은
2x2행렬에선 직선으로 표현된다.
결국 2x2행렬의 row picture의 해는 해당 직선들이 만나는 교점이다.

행렬의 각 row에 해당하는 방정식을 보는 것이 row picture이고
각 row방정식들의 교점을 찾는 것이 목표이자 시스템의 해라고 말한다.

2. Column picture
행렬에서 column부분을 보는 것이며 미지수벡터들의 종류들 끼리 각각 보는 것이다.

$\begin{bmatrix} 2 & -1\\ -1 & 2 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}= \begin{bmatrix} 0 \\ 3 \end{bmatrix}$


$x\begin{bmatrix} 2 \\ -1 \end{bmatrix}+ y\begin{bmatrix} -1 \\ 2 \end{bmatrix}= \begin{bmatrix} 0 \\ 3 \end{bmatrix}$

$a_x\overrightarrow{v_1} + a_y\overrightarrow{v_2}=u$

계수행렬에서 동일한 변수(미지수벡터)가 곱해지는 계수들을 묶어 정리한 것이다.
이렇게 정리한 결과는 계수행렬에서 column vector들과 각 변수의 곱으로 조합되어진다.

$u=a_1\overrightarrow{v_1} + a_2\overrightarrow{v_2}\dots + a_n\overrightarrow{v_n}$

위의 식처럼 이루어진 식을 선형결합이라고 부르며 선형대수의 근본이 되는 연산이다.

$x\begin{bmatrix} 2 \\ -1 \end{bmatrix}+ y\begin{bmatrix} -1 \\ 2 \end{bmatrix}= \begin{bmatrix} 0 \\ 3 \end{bmatrix}$

위의 시스템을 만족하는 해는 $x = 1, y=2$일때 이다.
row picture에서 구했던 교점과 같은 값이다.
이 해를 대입해서 식을 다시 쓰면

$1\begin{bmatrix} 2 \\ -1 \end{bmatrix}+ 2\begin{bmatrix} -1 \\ 2 \end{bmatrix}= \begin{bmatrix} 0 \\ 3 \end{bmatrix}$

로 나타낼 수 있고 이 column vector들이 공간상에서 표현하면 아래와 같다.

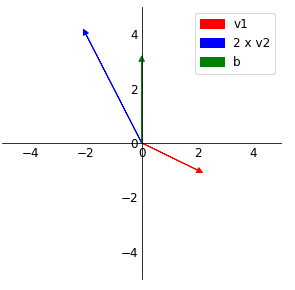
$v_2$벡터의 2배를 한 벡터를 공간상에서 이동시켜 $v_1,v_2$벡터의 합을 표현하면 아래와 같다.

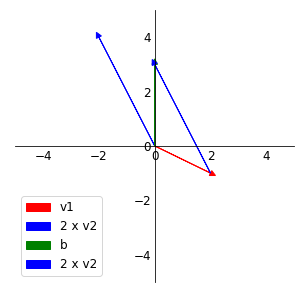
두 개의 벡터의 합이 b벡터를 표현하고 있는 것을 쉽게 알 수 있다.

$Ax=b$
어떤 시스템을 표현하는 matrix form A가 있고 미지수 벡터와 곱하여 b라는 결과를 만드는 식에서
row 방법은 내적(dot product)를 말하며
column 방법은 선형결합(linear combination)을 말한다.

row방법은 공간상에서 선이나 평면으로 표현이되고
column방법은 공간상에서 벡터들의 조합으로 표현된다.

2x2행렬이 아닌 3x3행렬을 생각해보면 좀 더 깊은 이해가 가능하다.

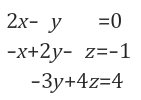
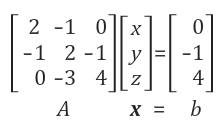
• row picture

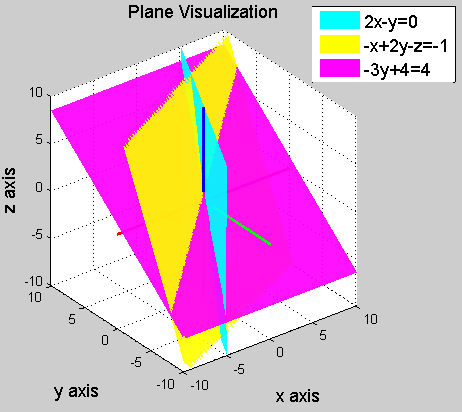
3x3행렬의 row picture은 공간상에서 평면으로 나타난다.
특수한 경우가 아니라면 ( 평면이나 교선이 평행또는일치 ) 두 평면은 한 교선에서 만나게 되고
위의 3개의 평면은 한점에서 만나게 된다. 이때 만나는 점을 시스템의 해라고 하며
(x=0, y=0, z=1)을 나타낸다.

• column picture

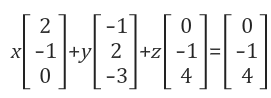
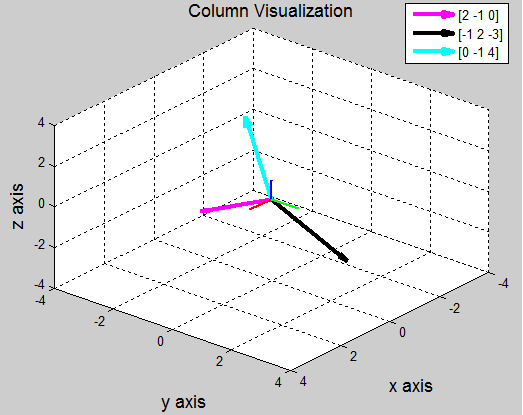
column 벡터들을 공간 상에 표시하면 위와 같이 나타낼 수 있다.
column 방식으로 표현했을때, z에 곱해진 벡터가 우변의 벡터와 같은 것을 한눈에 볼 수 있고
결과적으로 z벡터만 살리면 되겠다라고 생각할 수 있다.
따라서 x=0, y=0, z=1이란 해를 얻을 수 있다.

column방법으로 얻을 수 있는 정보는 매우 중요하다.
우측벡터의 값이 어떤 값이 들어와도 좌변들의 선형결합으로 만들 수 있을까?
이 생각은 매우 중요하다. 위의 시스템의 경우 모든 우변 벡터를 만들 수 있다.
그 이유는 무엇일까?
이유를 이해하기 위해서는 우선 2차원 평면에서 2개의 벡터가 만들 수 있는 벡터들에 대해서 생각해 볼 필요가 있다.

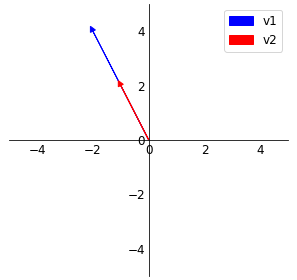첫 번째로 2개의 벡터가 같은 방향을 나타내고 있을 때이다.
이 벡터들끼리 어떤 조합으로 선형결합 ( 상수배, 덧셈 연산 ) 을 했을 때 결과는 평면상에 직선으로 나타난다. v1벡터에 상수배를해서 크기를 늘리건 줄이건, v2벡터에 상수배를해서 크기를 늘리건 줄이건 이들의 덧셈연산의 결과는 직선으로만 나타날 것 이다.

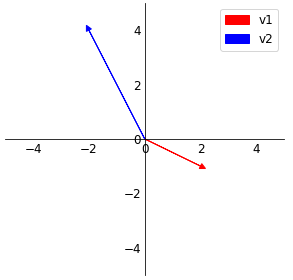
두 번째로 2개의 벡터가 다른 방향을 나타내고 있을 때 이 두 벡터의 선형결합으로 모든 xy좌표의 벡터를 나타낼 수 있다. v1,v2벡터에 상수배를하여 덧셈연산의 결과는 xy평면의 모든 점(벡터)를 표현할 수 있다.2차원 공간에서 이런 특징을 갖는 2개의 벡터를 선형독립의 관계에 있다고 말한다.

이 방식으로 3차원을 생각할 때, 3차원 공간에서 2개의 벡터(방향이 다른, 즉 선형독립인) 하나의 평면을 나타낼 것 이다.

이 상태에서 새로운 벡터가 추가될 때, 기존의 벡터가 생성할 수 있는 평면상에 존재할 경우 3개의 벡터의 선형결합의 결과는 바뀌지 않을 것이다. 3차원 공간에서 기존의 벡터2개의 조합으로 생성가능한 벡터를 선형종속의 관계에 있다고 말한다.
반대로 새로운 벡터가 추가 될때 2개의 벡터가 생성하지 못하는 벡터일 경우 3개의 벡터의 조합으로 3차원 공간의 모든 곳을 나타낼 수 있다. 즉 3개의 벡터가 선형독립인 관계에 있을 경우를 말한다.

래 질문으로 돌아가서 결국 이 3개의 벡터들은 전부 선형독립적인 관계에 있기 때문에 이 시스템은 우변 벡터가 무엇이 오든 전부 표현할 수 있다는 결론이 나오게 된다.