시계열 분석(Time Series Analysis) 소개

김민수·2024년 8월 22일

투빅스에서 발표를 기반으로 이글은 작성되었습니다.

안녕하세요!
오늘은 데이터 사이언스에서 매우 중요한 분야 중 하나인 시계열 분석에 대해 다뤄보겠습니다. 시계열 분석은 시간에 따라 변화하는 데이터를 다루는 방법으로, 다양한 응용 분야에서 활용되고 있습니다.

1. 시계열 분석이란?

시계열 데이터는 순차적인 시간의 흐름에 따라 기록된 데이터를 의미합니다. 예를 들어, 주가, 일별 기온, 월별 판매량 등이 시계열 데이터에 해당됩니다.

💡 핵심 질문: 과거 데이터가 미래에 어떤 영향을 미치는가?

시계열 데이터는 시간의 흐름에 따른 패턴을 분석하고 미래를 예측하는 데 활용됩니다.

2 시계열 분석의 중요성

시계열 분석의 가장 큰 목적은 '예측'입니다. 시간에 따른 데이터의 패턴을 이해함으로써, 미래에 발생할 수 있는 사건이나 경향을 예측할 수 있습니다.

📈 응용 분야: 주가 예측, 수요 예측, 음성 분석, 기후 변화 예측 등

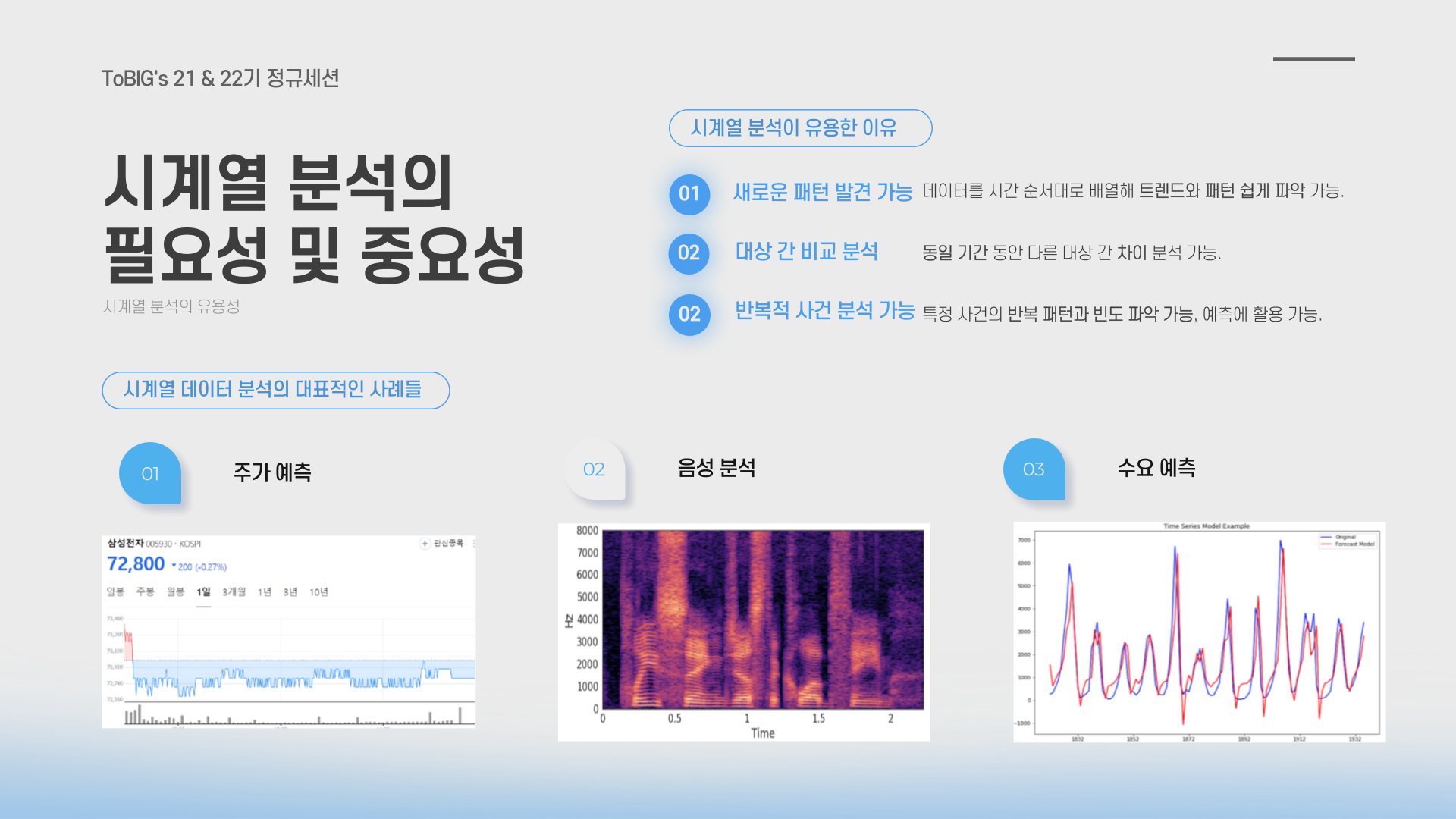
시계열 분석은 새로운 패턴을 발견하거나, 대상 간의 차이를 분석할 때, 그리고 반복적인 사건의 패턴을 파악할 때 매우 유용합니다.

3. 시계열 데이터의 4가지 요소

시계열 데이터를 효과적으로 분석하기 위해, 데이터는 보통 다음 4가지 요소로 분해됩니다

추세(T) - 시간의 흐름에 따라 장기적인 증가나 감소 경향

계절성(S) - 특정한 주기(예: 계절, 월, 주 등)마다 반복되는 패턴

주기(C) - 일정하지 않은 주기를 가지며, 경제적, 사회적 요인에 의해 발생하는 장기적인 변화.

잔차(R) - 위의 세 요소(T, S, C)로 설명되지 않는 불규칙한 변동.

🧩 시계열 데이터 분해식: Y = T + S + C + R

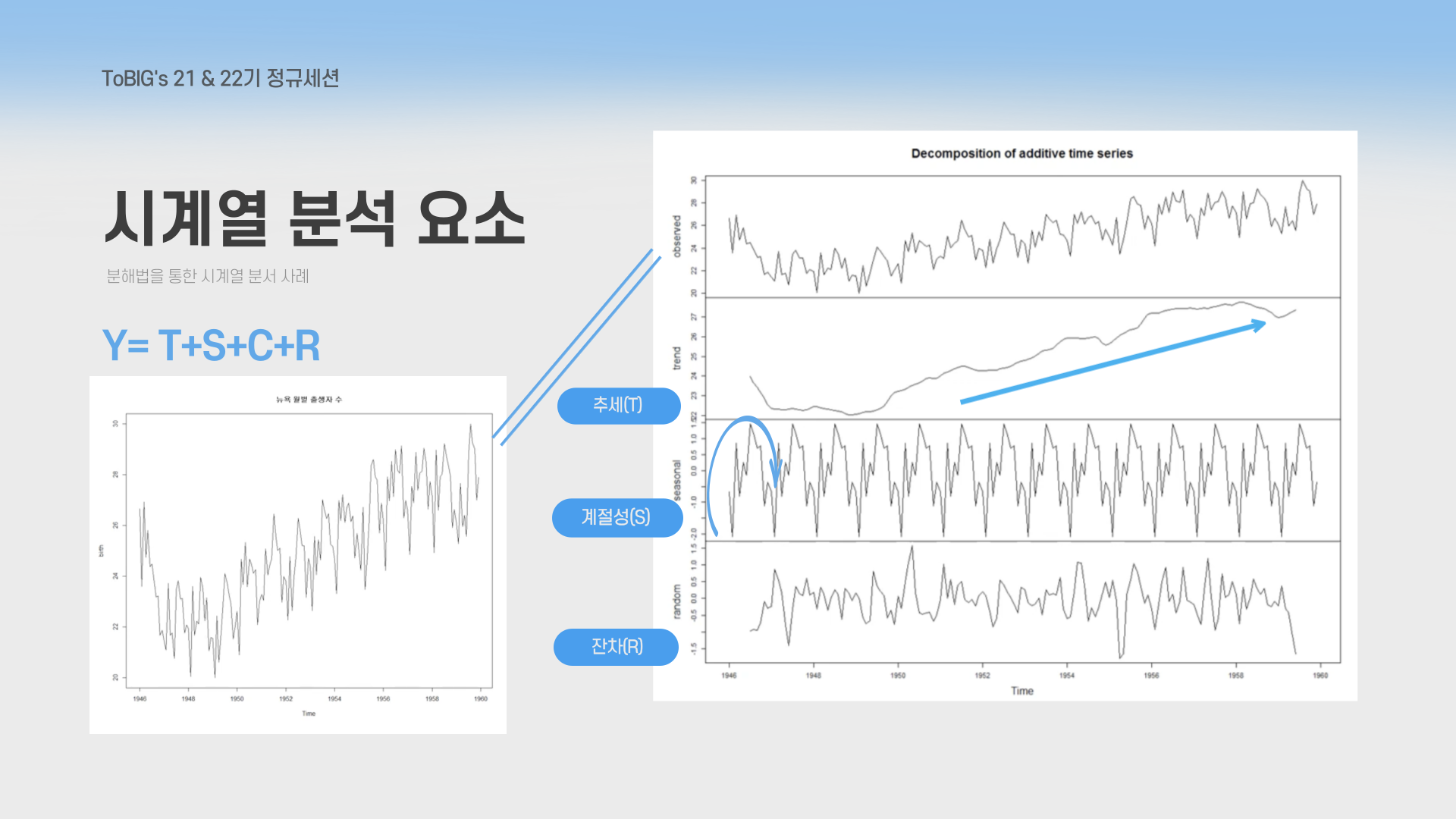
그래프는 시계열 데이터를 네 가지 요소로 분해하여 보여줍니다:

Observed (전체 데이터): 맨 위의 그래프는 관찰된 전체 시계열 데이터, 아래의 그래프에서 각각의 요소(추세, 계절성, 잔차)로 분해
Trend (추세, T): 이 그래프에서 볼 수 있듯이, 추세는 점진적으로 상승하고 있으며, 이는 전반적인 증가 경향을 시사
Seasonal (계절성, S): 이 그래프에서는 일정한 주기를 가지고 반복되는 변동 패턴을 확인
Residual (잔차, R): 이 그래프에서는 데이터의 예측 오차 또는 불규칙한 변동성을 볼 수 있음.

4. 시계열 분석의 주요 특징

시계열 데이터는 다음과 같은 주요 특징들을 가지고 있습니다. 각 특징은 시계열 분석에서 중요한 역할을 하며, 데이터의 패턴과 변동을 이해하는 데 도움을 줍니다.

특징	설명	중요한 이유
시간 의존성 (Temporal Dependency)	시간 순서대로 기록되며, 과거 값이 현재 값에 영향을 미침	과거 데이터가 미래 예측에 중요하기 때문에, 시간 순서 유지 필요
추세 (Trend)	장기적으로 증가하거나 감소하는 경향	데이터의 전반적인 방향성을 파악 가능
계절성 (Seasonality)	특정 주기로 반복되는 패턴 (예: 월별 판매량 변화)	주기적인 패턴을 고려한 예측 모델링 가능
비정상성 (Non-stationarity)	시간에 따라 평균이나 분산이 변함	차분(Differencing)이나 변환(Transformation)으로 안정화 필요
자기상관 (Autocorrelation)	과거 값이 미래 값을 예측하는 데 중요한 역할 (오늘 상태가 내일에 얼마나 영향을 미치는지)	자기상관성을 분석하여 모델 성능 개선

이러한 특징들은 시계열 데이터 분석에서 필수적으로 고려해야 할 요소들이며, 이를 통해 데이터를 더 정확하게 이해하고 예측할 수 있습니다.

5. 시계열 분석 요인

요인	설명	예시	시각적 표현
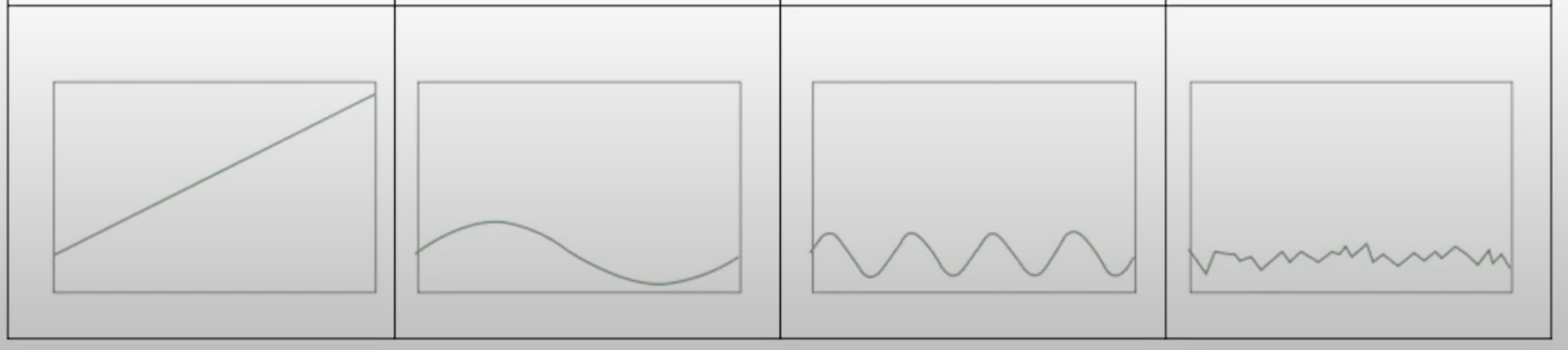
추세 요인 (Trend Factor)	장기간 혹은 점진적으로 상승하거나 하강하는 패턴	국내총생산(GDP), 인구증가율	꾸준히 증가하거나 감소하는 선형 그래프
순환 요인 (Cycle Factor)	특정 주기 혹은 수년 간격으로 발생하는 주기적인 패턴	경기 변동	주기적으로 상승과 하강을 반복하는 파형 그래프
계절 요인 (Seasonal Factor)	계절적 영향과 사회적 관습에 따라 1년 주기로 발생하는 패턴	추석, 설 등	주기적인 변동을 나타내는 그래프
불규칙 요인 (Irregular Factor)	명확히 설명할 수 없는 요인에 의한 우연한 패턴	전쟁, 홍수 등	불규칙한 변동을 나타내는 그래프

6. 시계열 데이터 분석 기법

시계열 분석에는 다양한 기법이 존재하며, 전통적인 방법과 확률적인 방법으로 나눌 수 있습니다. 전통적인 기법으로는 평활법과 분해법이 있으며, 확률적인 기법으로는 자기회귀(AutoRegression, AR), 이동평균(Moving Average, MA), 자기회귀이동평균(ARMA), 그리고 자기회귀누적이동평균(ARIMA) 모델이 있습니다.

구분	상세 기법
전통적 시계열 분석 기법	평활법 (Smoothing Method)
	분해법 (Decomposition Method)
확률적 시계열 분석 기법	자기회귀 모델 (AutoRegressive, AR)
	이동평균 모델 (Moving Average, MA)
	자기회귀 이동평균 모델 (AutoRegressive Moving Average, ARMA)
	자기회귀 누적 이동평균 모델 (AutoRegressive Integrated Moving Average, ARIMA)

이 표는 시계열 분석의 요인과 기법을 간결하게 정리하여 이해하기 쉽게 나타낸 것입니다.

7. 정상성

정상성은 시계열 데이터 분석에서 매우 중요한 개념으로, 시계열의 통계적 특성이 시간에 따라 변하지 않는 것을 의미합니다. 정상성을 가지는 시계열 데이터는 예측이 더 용이하며, 이를 위해 차분이나 변환이 필요할 수 있습니다.

7.1 정상성(Stationarity)의 정의

정상성은 시계열 데이터의 기본적 특성으로, 평균, 분산, 공분산 및 기타 모든 분포적 특성이 일정한 성질을 유지하는 것을 의미합니다. 시계열 자료는 시간의 흐름에 따라 관측된 데이터이며, 분석을 위해서는 정상성을 만족해야 합니다.

7.2 정상성의 3가지 조건

조건	설명
일정한 평균	모든 시점에 대해 일정한 평균을 가짐
일정한 분산	평균이 일정하지 않고 분산도 시점에 의존하지 않음
일정한 공분산	공분산도 단지 시차에만 의존할 뿐 실제 특정 시점에 의존하지 않음

7.3 정상성 변환 방법

상황	방법
추세가 보이거나 평균이 일정하지 않은 경우	- 차분(Difference)을 통해서 비정상 시계열을 가공
	- 1차 차분으로 정상성을 띠지 않으면 반복
분산이 일정하지 않은 경우	- 변환(Transformation)을 통해서 비정상 시계열을 가공
	- 로그 변환 등

8. 전통적 시계열 분석 기법

전통적인 시계열 분석 기법은 데이터의 특성을 파악하고, 데이터의 패턴을 예측하는 데 사용됩니다. 이러한 기법들은 주로 시계열 데이터의 잡음을 제거하거나, 데이터의 구성 요소를 분해하여 분석하는 데 중점을 둡니다. 전통적 시계열 분석 기법에는 평활법(Smoothing Method)과 분해법(Decomposition Method)이 있습니다.

평활법: 데이터의 잡음을 제거하고, 추세와 계절성을 쉽게 파악하기 위해 데이터를 평활화하는 방법입니다.

분해법: 시계열 데이터를 추세, 계절성, 주기, 잔차로 분해하여 각각의 구성 요소를 분석하는 방법입니다

8.1 평활법 (Smoothing Method)

평활법은 시계열 데이터에서 불규칙한 변동을 평탄하게 만들어 데이터의 추세와 패턴을 파악하고, 예측값을 계산하는 방법입니다. 데이터의 잡음을 줄이고, 중요한 패턴을 더 명확히 드러내는 데 사용됩니다. 평활법에는 이동평균법(Moving Average Method)과 지수평활법(Exponential Smoothing Method)이 있습니다.

1) 이동평균법 (Moving Average Method)

정의: 이동평균법은 과거부터 현재까지의 시계열 데이터를 일정 기간별로 평균을 계산하여 추세를 파악하고, 이를 바탕으로 미래 값을 예측하는 방법입니다.

설명:
- 이동평균법은 일정한 기간 내의 관측값을 평균하여 데이터를 평활화(smooth)합니다. 이를 통해 단기적인 잡음(noise)을 제거하고, 장기적인 추세를 파악할 수 있습니다.
- 예측값은 이동평균으로 계산되며, 주로 간단한 예측을 위해 사용됩니다.
- 가중 이동평균법(Weighted Moving Average Method)은 더 최근의 데이터에 더 많은 가중치를 부여하여, 최근 변화가 예측에 더 큰 영향을 미치도록 하는 방법입니다.
수식:
특징:
- 단순 이동평균법(Simple Moving Average Method): 모든 데이터에 동일한 가중치를 부여하여 평균을 계산.
- 가중 이동평균법(Weighted Moving Average Method): 최근 데이터를 더 중요하게 여기며, 최근 데이터에 더 높은 가중치를 부여.
장점:
- 간단하고 쉽게 계산할 수 있으며, 급격한 데이터 변동을 줄여줌.
단점:
- 이동평균 계산에 사용하는 데이터 기간의 설정에 따라 결과가 달라질 수 있으며, 데이터의 장기적 추세를 예측하기 어려움.

2) 지수평활법 (Exponential Smoothing Method)

정의: 지수평활법은 시간의 흐름에 따라 최근의 시계열 데이터에 더 많은 가중치(지수평활계수, α)를 부여하여 미래를 예측하는 방법입니다.

설명:
- 지수평활법은 과거 데이터의 중요도를 점차 줄여가며, 최근 데이터의 변화에 더 큰 비중을 두는 방식입니다.
- 이는 데이터의 장기적인 추세를 더 잘 반영하고, 급격한 변화를 더 빠르게 반영할 수 있습니다.
- 지수평활법은 단순 지수평활법(Simple Exponential Smoothing), 이중 지수평활법(Double Exponential Smoothing), 삼중 지수평활법(Triple Exponential Smoothing) 등으로 확장됩니다.
수식:
특징:
- 지수평활 계수 α의 값에 따라 예측의 민감도가 결정됩니다. α가 크면 최근 데이터에 더 많은 비중을 두며, 작으면 오래된 데이터의 영향도 고려됩니다.
장점:
- 계산이 간단하며, 이동평균법보다 유연하고, 최신 데이터를 더 반영하여 예측 정확도를 높임.

단점:

α 값의 선택이 예측 정확도에 큰 영향을 미치며, 주기적인 변동을 가진 데이터에는 적합하지 않음.

import pandas as pd
import matplotlib.pyplot as plt
data = pd.Series([100, 102, 101, 105, 110, 115, 117, 120, 125, 130])
moving_avg = data.rolling(window=3).mean()
plt.plot(data, label='Original Data')
plt.plot(moving_avg, label='Moving Average (window=3)', color='red')
plt.legend()
plt.show()

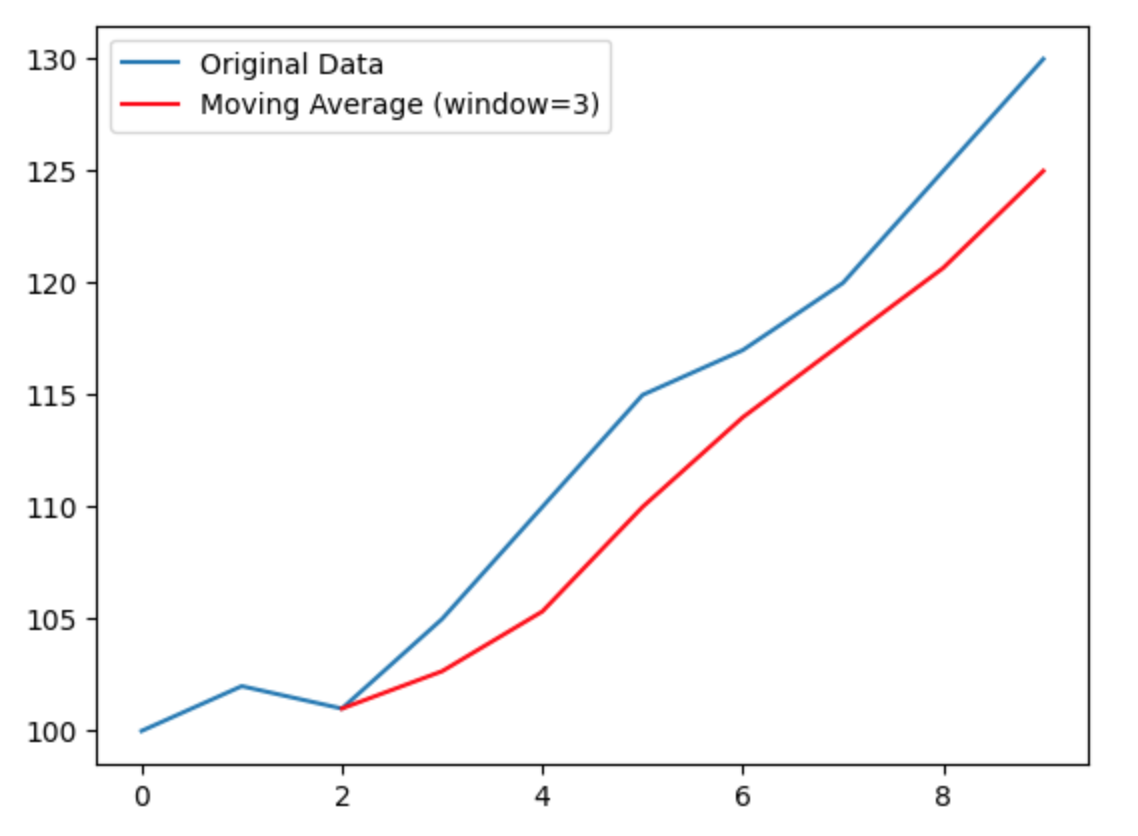
8.2 분해법 (Decomposition Method)

분해법은 시계열 데이터를 여러 구성 요소로 나누어 분석하는 방법입니다. 주로 데이터의 추세, 계절성, 순환성, 그리고 불규칙성을 분리하여 각 요소를 독립적으로 분석합니다. 이를 통해 데이터의 특성을 더 잘 이해하고, 예측 모델의 성능을 높일 수 있습니다.

정의: 시계열 데이터를 추세 요인, 계절 요인, 순환 요인, 잔차 요인으로 분해하여 각 구성 요소의 패턴을 분석하는 기법.

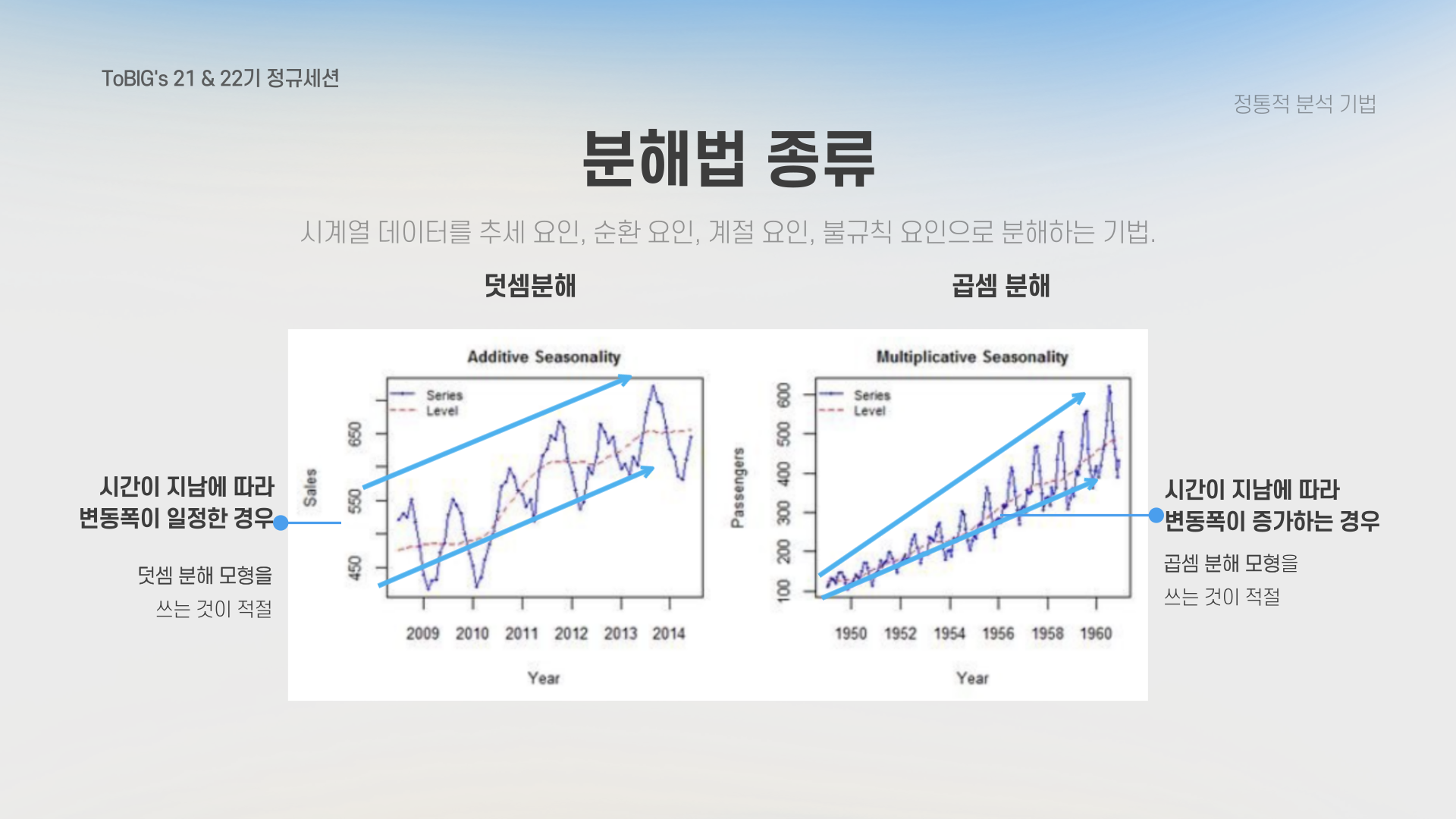
1) 덧셈분해 (Additive Decomposition)

정의: 시계열 데이터의 변동폭이 시간의 흐름에 관계없이 일정한 경우에 사용합니다.

설명:
- 덧셈분해 모델은 시계열 데이터를 네 가지 요소, 즉 추세(T), 계절성(S), 순환성(C), 그리고 잔차(R)로 분해하여 나타냅니다.
- 시계열의 전체 데이터는 다음과 같이 표현됩니다:
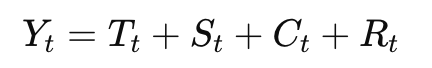
- 덧셈분해는 변동폭이 일정하고, 계절적 패턴이 유지되는 데이터를 분석하는 데 적합합니다.
특징:
- 데이터의 변동이 시간에 따라 일정한 패턴을 보일 때 사용.
- 예: 일별 판매량이 매일 유사한 변동폭을 보일 때 사용.

2) 곱셈분해 (Multiplicative Decomposition)

정의: 시계열 데이터의 변동폭이 시간의 흐름에 따라 점차로 커지는 경우에 사용합니다.

설명:
- 곱셈분해 모델은 시계열 데이터의 네 가지 요소가 곱의 형태로 결합된 것으로 가정합니다.
- 시계열의 전체 데이터는 다음과 같이 표현됩니다:
- 곱셈분해는 변동폭이 시간이 지남에 따라 점차 커지는 데이터를 분석하는 데 적합합니다.
특징:
- 데이터의 변동이 시간이 지남에 따라 점진적으로 증가하거나 감소할 때 사용.
- 예: 주가 데이터나 인플레이션이 반영된 경제 데이터에서 변동폭이 커지는 경우.

    from statsmodels.tsa.seasonal 
    import seasonal_decompose
    data = pd.Series([10, 12, 15, 13, 18, 20, 24, 28, 35, 40], index=pd.date_range('2024-01-01', periods=10, freq='M'))
    result = seasonal_decompose(data, model='additive', period=1)
    result.plot()
    plt.show()

업로드중..

분해법은 시계열 데이터의 주요 구성 요소를 분리하여 분석하고, 각 요소의 패턴을 명확히 파악함으로써 데이터를 더 잘 이해하고, 예측 정확도를 높이는 데 도움을 줍니다.

9. 확률적 시계열 분석 기법

확률적 시계열 분석 기법은 데이터의 과거 값이나 오차를 이용하여 미래를 예측하는 모델링 방법입니다. 주로 자기회귀(AR), 이동평균(MA), 그리고 두 모델을 결합한 ARMA 및 ARIMA 모델이 있습니다.

9.1 자기회귀 모델 (AutoRegression, AR)

정의: 자기회귀 모델(AR)은 과거의 관측값을 사용하여 현재의 값을 예측하는 모델입니다. 이전 시점들의 데이터가 현재 시점에 얼마나 영향을 미치는지 분석하는 방법으로, 과거 데이터에 대한 의존성을 반영합니다.

수식:
설명: AR 모델은 과거 데이터의 가중합을 기반으로 현재의 값을 예측합니다. 여기서 가중치는 회귀 계수로 결정되며, 이는 모델의 학습 과정에서 추정됩니다.
특징: AR 모델은 자기상관함수(ACF)가 지수적으로 감소하고, 부분 자기상관함수(PACF)가 특정 시점 이후에 절단(cut off)되는 형태를 보입니다.

9.2 이동평균 모델 (Moving Average, MA)

정의: 이동평균 모델(MA)은 과거의 예측 오차(잔차)를 사용하여 현재의 값을 예측하는 모델입니다. 과거의 오차 항들의 선형 결합으로 미래 값을 추정합니다.

수식:
설명: MA 모델은 이전의 오차 값들이 현재의 데이터 값에 어떻게 영향을 미치는지를 기반으로 예측합니다. 이는 백색 잡음의 가중 합으로 미래 값을 계산합니다.
특징: MA 모델의 자기상관함수(ACF)는 특정 시점에서 절단(cut off)되고, 부분 자기상관함수(PACF)는 지수적으로 감소하는 형태를 보입니다.

9.3 자기회귀이동평균 모델 (AutoRegressive Moving Average, ARMA)

정의: ARMA 모델은 자기회귀(AR)와 이동평균(MA) 모델을 결합한 형태로, 과거의 데이터 값과 오차 값을 모두 사용하여 현재의 값을 예측합니다.

수식:
설명: ARMA 모델은 AR 모델의 과거 값들과 MA 모델의 오차 항을 동시에 고려하여 예측의 정확성을 높입니다. 이는 시계열 데이터의 패턴을 더 잘 설명할 수 있는 유연한 모델입니다.
특징: ARMA 모델은 일반적으로 ACF와 PACF가 모두 지수적으로 감소하거나 특정 패턴을 보이는 경우에 적합합니다.

9.4 자기회귀누적이동평균 모델 (AutoRegressive Integrated Moving Average, ARIMA)

정의: ARIMA 모델은 ARMA 모델에 차분(Differencing)을 추가하여 비정상(Non-stationary) 시계열 데이터를 정상(Stationary) 시계열 데이터로 변환해 분석하는 기법입니다.

수식:
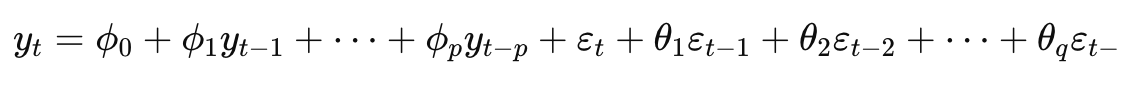
설명: ARIMA 모델은 시계열 데이터가 정상성을 띠지 않을 때, 차분을 통해 이를 정상화한 후, ARMA 모델을 적용합니다. 이를 통해 시계열의 추세를 제거하고 예측의 정확성을 높입니다.
특징: ARIMA 모델의 주요 하이퍼파라미터는 (p) (AR 차수), (d) (차분 차수), (q) (MA 차수)입니다. 적절한 차수 선택이 모델의 성능에 큰 영향을 미칩니다.

이렇게 AR, MA, ARMA, 그리고 ARIMA 모델은 시계열 데이터의 다양한 특성과 패턴을 설명하고 예측하기 위해 사용됩니다. 각 모델의 특성에 따라 적절한 기법을 선택하는 것이 중요합니다.

자기회귀 모델(AR): 과거 값들이 현재 값에 미치는 영향을 모델링합니다.

이동평균 모델(MA): 잔차의 선형 결합을 통해 미래 값을 예측합니다.

자기회귀이동평균 모델(ARMA): 자기회귀와 이동평균 모델을 결합하여 시계열 데이터를 설명합니다.

자기회귀누적이동평균 모델(ARIMA): 비정상 시계열 데이터를 정상화한 후 ARMA 모델을 적용하는 방법입니다.

10. ACF(자기상관함수)와 PACF(부분자기상관함수)

10.1 ACF (AutoCorrelation Function)란?

정의: ACF는 시계열의 관측치 간 상관계수를 나타냅니다. 주어진 시간 시차(lag) ( k )에 대한 시계열 데이터 간의 상관성을 계산하여, 시간이 흐름에 따라 데이터가 얼마나 관련이 있는지를 보여줍니다.
정상 시계열 데이터: ACF가 상대적으로 빠르게 0에 접근합니다. 이는 데이터가 시간이 지남에 따라 독립적임을 의미합니다.
비정상 시계열 데이터: ACF가 천천히 감소하며 큰 양의 값을 유지합니다. 이는 시간이 지남에 따라 강한 자기상관을 가짐을 나타냅니다.

10.2 PACF (Partial AutoCorrelation Function)란?

정의: PACF는 ACF와 유사하게 시계열 관측치 간의 상관 관계를 나타내지만, 다른 모든 중간 시차의 영향을 제거한 '순수한' 상관관계를 보여줍니다. 특정 시차 ( k )에서의 상관 관계를 직접 측정하여 데이터의 순차적 관계를 파악합니다.
활용: PACF는 AR 모델을 설정할 때 주로 사용되며, 특정 시차에서 값이 급격히 감소하는 경우 AR(p) 모델을 고려할 수 있습니다.

10.3 ACF와 PACF의 활용 예제

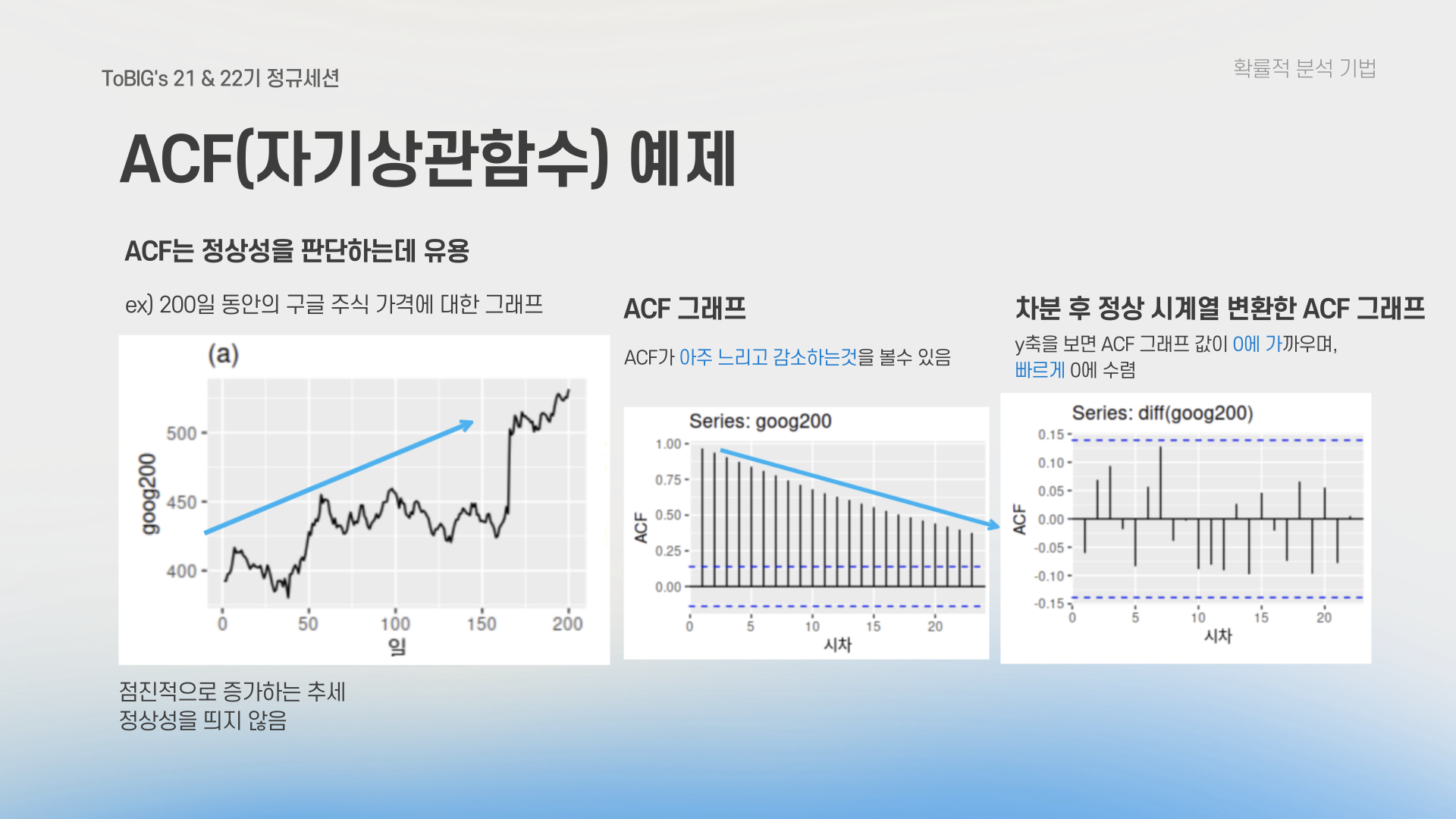
ACF 그래프는 데이터의 정상성 여부를 판단하는 데 유용합니다. 예를 들어, 비정상 시계열 데이터의 ACF는 천천히 감소하는 경향이 있습니다.
차분 후 ACF 그래프를 통해 데이터가 정상화되었는지를 확인할 수 있습니다. 차분을 통해 ACF가 빠르게 0에 수렴하면, 데이터가 정상 시계열로 변환되었음을 의미합니다.

ACF와 PACF의 활용: 모델 결정

AR(p) 모델: ACF는 천천히 감소하고, PACF는 특정 시차에서 급격히 줄어듭니다.
MA(q) 모델: ACF는 특정 시차 후 급격히 0에 가깝게 줄어들고, PACF는 천천히 감소합니다.
ARMA(p, q) 모델: ACF와 PACF 모두 특정 시차 이후에 소멸(die out)하는 패턴을 보입니다.

이러한 ACF와 PACF의 패턴을 통해, 시계열 데이터를 적합한 모델로 분석하고 예측할 수 있습니다.

마치며

이 글이 시계열 분석을 공부하는 데에 도움이 되었길 바라며, 앞으로도 이와 같은 다양한 데이터 분석 기법들을 적극적으로 활용해 보시길 추천드립니다. 감사합니다!

김민수

데이터 분석과 인공지능을 공부하고 있습니다.

이전 포스트