malloc과 포인터
아래와 같은 main 함수 코드가 있습니다. 여기서 문제가 될 만한 지점을 발견할 수 있나요?
int main(void)
{
int *x;
int *y;
x = malloc(sizeof(int));
*x = 42;
*y = 13;
}main 함수 안의 첫 두 줄에서는 포인터 x와 y를 선언합니다. 그리고 x에는 malloc 함수를 이용해서 int 자료형 크기에 해당하는 메모리를 할당합니다. 그 다음에는 x와 y 포인터가 가리키는 지점에 각각 42와 13을 저장합니다.
여기서 문제가 될 만한 부분은 *y = 13 입니다. y는 포인터로만 선언되었을 뿐이지, 어디를 가리킬지에 대해서는 아직 정의가 되지 않았습니다.
따라서 초기화 되지 않은 *y는 프로그램 어딘가를 임의로 가리키고 있을 수도 있습니다. 따라서 그 곳에 13이라는 값을 저장하는 것이 오류를 발생시킬 수도 있는 것이죠.
아래 코드와 같이 y = x; 라는 코드를 더해주면, y는 x가 가리키는 곳과 동일한 곳을 가리키게 됩니다. 따라서 *y = 13; 으로 저장하면 x가 가리키는 곳에도 동일하게 13으로 저장될 것입니다.
y = x;
*y = 13;배열의 크기 조정하기
일정한 크기의 배열이 주어졌을 때, 그 크기를 키우려면 어떻게 해야 할까요?
단순하게 현재 배열이 저장되어 있는 메모리 위치의 바로 옆에 일정 크기의 메모리를 더 덧붙이면 되겠지만, 실제로는 다른 데이터가 저장되어 있을 확률이 높습니다.
따라서 안전하게 새로운 공간에 큰 크기의 메모리를 다시 할당하고 기존 배열의 값들을 하나씩 옮겨줘야 합니다.
이런 작업은 O(n), 즉 배열의 크기 n만큼의 실행 시간이 소요될 것입니다.
이 과정을 아래 코드와 같이 나타낼 수 있습니다.
#include <stdio.h>
#include <stdlib.h>
int main(void)
{
//int 자료형 3개로 이루어진 list 라는 포인터를 선언하고 메모리 할당
int *list = malloc(3 * sizeof(int));
// 포인터가 잘 선언되었는지 확인
if (list == NULL)
{
return 1;
}
// list 배열의 각 인덱스에 값 저장
list[0] = 1;
list[1] = 2;
list[2] = 3;
//int 자료형 4개 크기의 tmp 라는 포인터를 선언하고 메모리 할당
int *tmp = malloc(4 * sizeof(int));
if (tmp == NULL)
{
return 1;
}
// list의 값을 tmp로 복사
for (int i = 0; i < 3; i++)
{
tmp[i] = list[i];
}
// tmp배열의 네 번째 값도 저장
tmp[3] = 4;
// list의 메모리를 초기화
free(list);
// list가 tmp와 같은 곳을 가리키도록 지정
list = tmp;
// 새로운 배열 list의 값 확인
for (int i = 0; i < 4; i++)
{
printf("%i\n", list[i]);
}
// list의 메모리 초기화
free(list);
} 위와 동일한 작업을 realloc 이라는 함수를 이용해서 수행할 수도 있습니다.
#include <stdio.h>
#include <stdlib.h>
int main(void)
{
int *list = malloc(3 * sizeof(int));
if (list == NULL)
{
return 1;
}
list[0] = 1;
list[1] = 2;
list[2] = 3;
// tmp 포인터에 메모리를 할당하고 list의 값 복사
int *tmp = realloc(list, 4 * sizeof(int));
if (tmp == NULL)
{
return 1;
}
// list가 tmp와 같은 곳을 가리키도록 지정
list = tmp;
// 새로운 list의 네 번째 값 저장
list[3] = 4;
// list의 값 확인
for (int i = 0; i < 4; i++)
{
printf("%i\n", list[i]);
}
//list 의 메모리 초기화
free(list);
}연결 리스트: 도입
데이터 구조
데이터 구조는 우리가 컴퓨터 메모리를 더 효율적으로 관리하기 위해 새로 정의하는 구조체입니다. 일종의 메모리 레이아웃, 또는 지도라고 생각할 수 있습니다.
데이터 구조중 하나인 연결 리스트에 대해 알아보겠습니다
연결 리스트
배열에서는 각 인덱스의 값이 메모리상에서 연이어 저장되어 있습니다. 하지만 꼭 그럴 필요가 있을까요? 각 값이 메모리상의 여러 군데 나뉘어져 있다고 하더라도 바로 다음 값의 메모리 주소만 기억하고 있다면 여전히 값을 연이어서 읽어들일 수 있습니다.
이를 ‘연결 리스트’라고 합니다. 아래 그림과 같이 크기가 3인 연결 리스트는 각 인덱스의 메모리 주소에서 자신의 값과 함께 바로 다음 값의 주소(포인터)를 저장합니다.
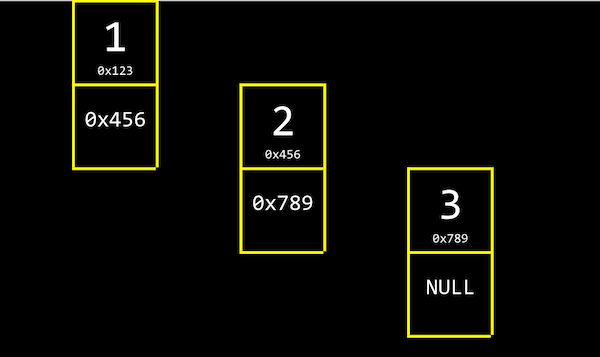
연결 리스트의 가장 첫 번째 값인 1은 2의 메모리 주소를, 2는 3의 메모리 주소를 함께 저장하고 있습니다. 3은 다음 값이 없기 때문에 NULL (\0, 즉 0으로 채워진 값을 의미합니다)을 다음 값의 주소로 저장합니다.
연결 리스트는 아래 코드와 같이 간단한 구조체로 정의할 수 있습니다.
typedef struct node
{
int number;
struct node *next;
}
node;
node 라는 이름의 구조체는 number 와 *next 두 개의 필드가 함께 정의되어 있습니다. number는 각 node가 가지는 값, *next 는 다음 node를 가리키는 포인터가 됩니다.
여기서 typedef struct 대신에 typedef struct node 라고 ‘node’를 함께 명시해 주는 것은, 구조체 안에서 node를 사용하기 위함입니다.
연결 리스트: 코딩
앞서 정의한 구조체를 활용해서 실제로 연결 리스트를 구현해보도록 하겠습니다.
#include <stdio.h>
#include <stdlib.h>
//연결 리스트의 기본 단위가 되는 node 구조체를 정의합니다.
typedef struct node
{
//node 안에서 정수형 값이 저장되는 변수를 name으로 지정합니다.
int number;
//다음 node의 주소를 가리키는 포인터를 *next로 지정합니다.
struct node *next;
}
node;
int main(void)
{
// list라는 이름의 node 포인터를 정의합니다. 연결 리스트의 가장 첫 번째 node를 가리킬 것입니다.
// 이 포인터는 현재 아무 것도 가리키고 있지 않기 때문에 NULL 로 초기화합니다.
node *list = NULL;
// 새로운 node를 위해 메모리를 할당하고 포인터 *n으로 가리킵니다.
node *n = malloc(sizeof(node));
if (n == NULL)
{
return 1;
}
// n의 number 필드에 1의 값을 저장합니다. “n->number”는 “(*n).numer”와 동일한 의미입니다.
// 즉, n이 가리키는 node의 number 필드를 의미하는 것입니다.
// 간단하게 화살표 표시 ‘->’로 쓸 수 있습니다. n의 number의 값을 1로 저장합니다.
n->number = 1;
// n 다음에 정의된 node가 없으므로 NULL로 초기화합니다.
n->next = NULL;
// 이제 첫번째 node를 정의했기 떄문에 list 포인터를 n 포인터로 바꿔 줍니다.
list = n;
// 이제 list에 다른 node를 더 연결하기 위해 n에 새로운 메모리를 다시 할당합니다.
n = malloc(sizeof(node));
if (n == NULL)
{
return 1;
}
// n의 number와 next의 값을 각각 저장합니다.
n->number = 2;
n->next = NULL;
// list가 가리키는 것은 첫 번째 node입니다.
//이 node의 다음 node를 n 포인터로 지정합니다.
list->next = n;
// 다시 한 번 n 포인터에 새로운 메모리를 할당하고 number과 next의 값을 저장합니다.
n = malloc(sizeof(node));
if (n == NULL)
{
return 1;
}
n->number = 3;
n->next = NULL;
// 현재 list는 첫번째 node를 가리키고, 이는 두번째 node와 연결되어 있습니다.
// 따라서 세 번째 node를 더 연결하기 위해 첫 번째 node (list)의
// 다음 node(list->next)의 다음 node(list->next->next)를 n 포인터로 지정합니다.
list->next->next = n;
// 이제 list에 연결된 node를 처음부터 방문하면서 각 number 값을 출력합니다.
// 마지막 node의 next에는 NULL이 저장되어 있을 것이기 때문에 이 것이 for 루프의 종료 조건이 됩니다.
for (node *tmp = list; tmp != NULL; tmp = tmp->next)
{
printf("%i\n", tmp->number);
}
// 메모리를 해제해주기 위해 list에 연결된 node들을 처음부터 방문하면서 free 해줍니다.
while (list != NULL)
{
node *tmp = list->next;
free(list);
list = tmp;
}
}연결 리스트: 시연
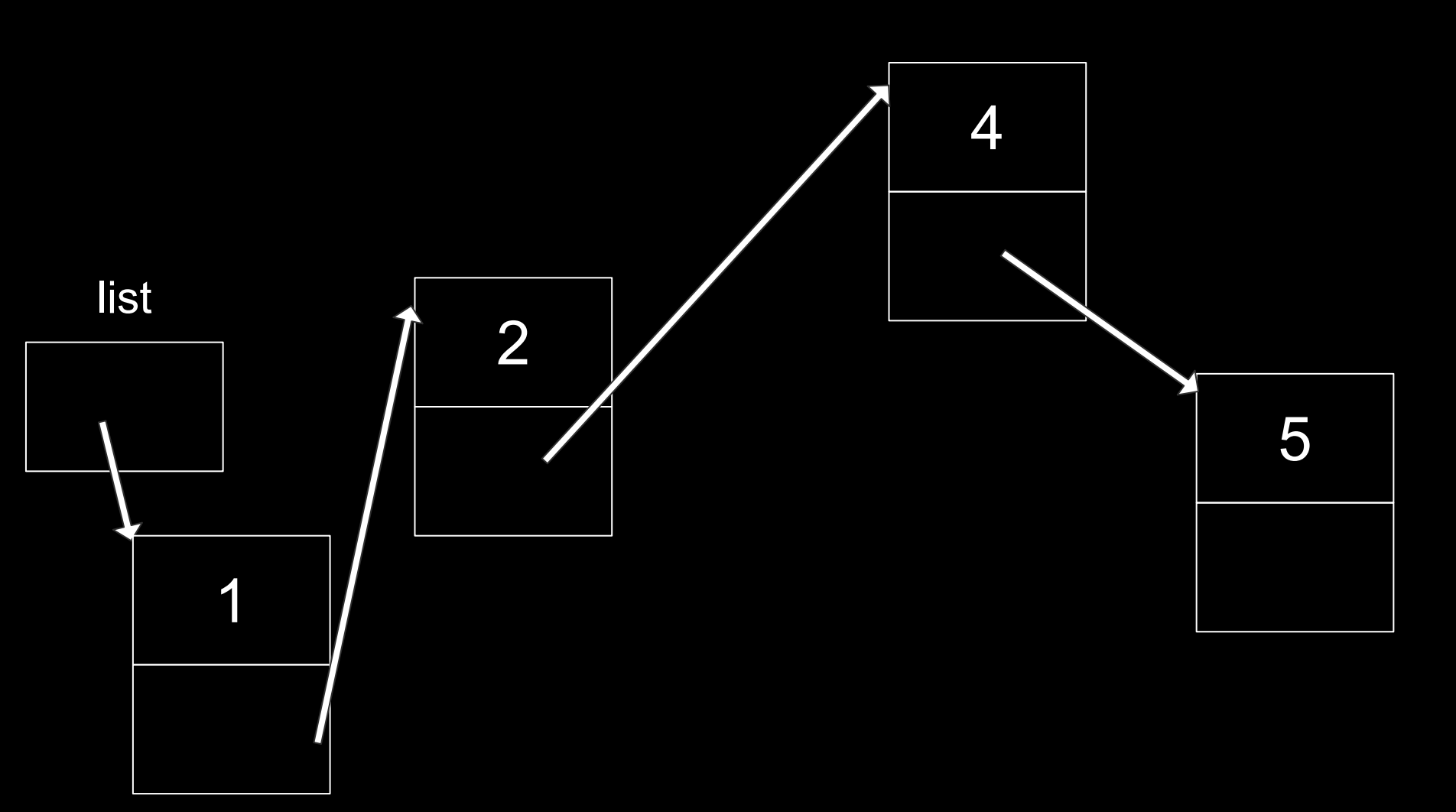
연결 리스트 예시 이미지 입니다.
연결 리스트의 장단점
배열과 비교해서 연결 리스트는 새로운 값을 추가할 때 다시 메모리를 할당하지 않아도 된다는 장점이 있습니다. 하지만 이런 유동적인 구조는 그 대가가 따릅니다. 구조가 정적인 배열과 달리 연결 리스트에서는 임의 접근이 불가능합니다.
연결 리스트에 값을 추가하거나 검색하는 경우를 생각해 봅시다. 이를 위해서는 해당하는 위치까지 연결 리스트의 각 node들을 따라 이동해야 합니다. 따라서 연결 리스트의 크기가 n 일때 그 실행 시간은 O(n)이 됩니다.
배열의 경우 임의 접근이 가능하기 때문에 (정렬 되어 있는 경우) 이진 검색을 이용하면 O(log n)의 실행 시간이 소요 되는 것에 비해서 다소 불리합니다.
이처럼 여러 데이터 구조는 각각 장단점이 존재합니다. 프로그래밍을 할 때 목적에 부합하는 가장 효율적인 데이터 구조를 고민해서 사용하는 것이 중요합니다.
연결 리스트: 트리
트리는 연결 리스트를 기반으로 한 새로운 데이터 구조입니다.
연결리스트에서의 각 노드 (연결 리스트 내의 한 요소를 지칭)들의 연결이 1차원적으로 구성되어 있다면, 트리에서의 노드들의 연결은 2차원적으로 구성되어 있다고 볼 수 있습니다. 각 노드는 일정한 층에 속하고, 다음 층의 노드들을 가리키는 포인터를 가지게 됩니다.
아래 그림은 트리의 한 예입니다. 나무가 거꾸로 뒤집혀 있는 형태를 생각하면 됩니다.
- 가장 높은 층에서 트리가 시작되는 노드를 ‘루트’라고 합니다.
- 루트 노드는 다음 층의 노드들을 가리키고 있고, 이를 ‘자식 노드’라고 합니다.
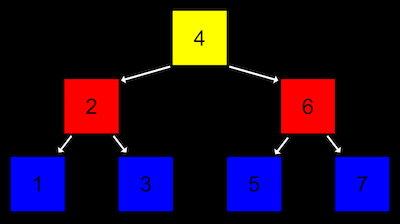
위 그림에 묘사된 트리는 구체적으로 ‘이진 검색 트리’ 입니다. 각 노드가 구성되어 있는 구조를 살펴보면 일정한 규칙을 알 수 있습니다.
- 먼저 하나의 노드는 두 개의 자식 노드를 가집니다.
- 또 왼쪽 자식 노드는 자신의 값 보다 작고, 오른쪽 자식 노드는 자신의 값보다 큽니다.
- 따라서 이런 트리 구조는 이진 검색을 수행하는데 유리합니다.
아래 코드에서는 이진 검색 트리의 노드 구조체와 “50”을 재귀적으로 검색하는 이진 검색 함수를 구현하였습니다.
//이진 검색 트리의 노드 구조체
typedef struct node
{
// 노드의 값
int number;
// 왼쪽 자식 노드
struct node *left;
// 오른쪽 자식 노드
struct node *right;
} node;
// 이진 검색 함수 (*tree는 이진 검색 트리를 가리키는 포인터)
bool search(node *tree)
{
// 트리가 비어있는 경우 ‘false’를 반환하고 함수 종료
if (tree == NULL)
{
return false;
}
// 현재 노드의 값이 50보다 크면 왼쪽 노드 검색
else if (50 < tree->number)
{
return search(tree->left);
}
// 현재 노드의 값이 50보다 작으면 오른쪽 노드 검색
else if (50 > tree->number)
{
return search(tree->right);
}
// 위 모든 조건이 만족하지 않으면 노드의 값이 50이므로 ‘true’ 반환
else {
return true;
}
}
이진 검색 트리를 활용하였을 때 검색 실행 시간과 노드 삽입 시간은 모두 O(log n) 입니다.
해시 테이블
해시 테이블은 ‘연결 리스트의 배열’입니다. 여러 값들을 몇 개의 바구니에 나눠 담는 상황을 생각해 봅시다.
각 값들은 ‘해시 함수’라는 맞춤형 함수를 통해서 어떤 바구니에 담기는 지가 결정 됩니다. 각 바구니에 담기는 값들은 그 바구니에서 새롭게 정의되는 연결 리스트로 이어집니다. 이와 같이 연결 리스트가 담긴 바구니가 여러개 있는 것이 ‘연결 리스트의 배열’, 즉 ‘해시 테이블’이 됩니다.
쉬운 예로 아래 그림과 같이 사람의 이름이 해시 테이블에 저장되며, 해시 함수는 ‘이름의 가장 첫 글자’인 경우를 생각해 보겠습니다.
그 경우 알파벳 개수에 해당하는 총 26개의 포인터들이 있을 수 있으며, 각 포인터는 그 알파벳을 시작으로 하는 이름들을 저장하는 연결 리스트를 가리키게 됩니다.
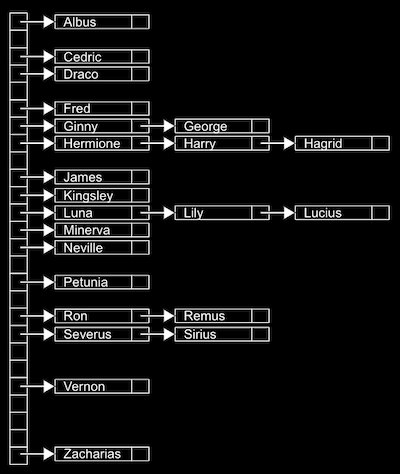
만약 해시 함수가 이상적이라면, 각 바구니에는 단 하나의 값들만 담기게 될 것입니다. 따라서 검색 시간은 O(1)이 됩니다. 하지만 그렇지 않은 경우, 최악의 상황에는 단 하나의 바구니에 모든 값들이 담겨서 O(n)이 될 수도 있습니다.
일반적으로는 최대한 많은 바구니를 만드는 해시 함수를 사용하기 때문에 거의 O(1)에 가깝다고 볼 수 있습니다.
트라이
‘트라이’는 기본적으로 ‘트리’ 형태의 자료 구조입니다. 특이한 점은 각 노드가 ‘배열’로 이루어져있다는 것입니다.
예를 들어 영어 알파벳으로 이루어진 문자열 값을 저장한다고 한다면 이 노드는 a부터 z까지의 값을 가지는 배열이 됩니다. 그리고 배열의 각 요소, 즉 알파벳은 다음 층의 노드(a-z 배열)를 가리킵니다.
아래 그림과 같이 Hermione, Harry, Hagrid 세 문자열을 트라이에 저장해보겠습니다. 루트 노드를 시작으로 각 화살표가 가리키는 알파벳을 따라가면서 노드를 이어주면 됩니다.
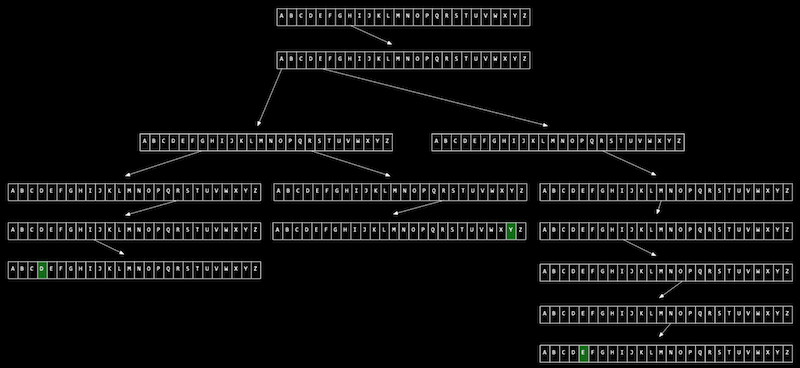
위와 같은 트라이에서 값을 검색하는데 걸리는 시간은 ‘문자열의 길이’에 의해 한정됩니다. 단순히 문자열의 각 문자를 보며 트리를 탐색해나가기만 하면 되니까요.
일반적인 영어 이름의 길이를 n이라고 했을 때, 검색 시간은 O(n)이 되지만, 대부분의 이름은 그리 크지 않은 상수값(예, 20자 이내)이기 때문에 O(1)이나 마찬가지라고 볼 수 있습니다.
스택, 큐, 딕셔너리
큐
큐는 메모리 구조에서 살펴봤듯이 값이 아래로 쌓이는 구조입니다. 값을 넣고 뺄 때 ‘선입 선출’ 또는 ‘FIFO (First in First Out)’라는 방식을 따르게 됩니다. 가장 먼저 들어온 값이 가장 먼저 나가는 것이죠.
은행에서 줄을 설 때 가장 먼저 줄을 선 사람이 가장 먼저 업무를 처리하게 되는 것과 동일합니다. 배열이나 연결 리스트를 통해 구현 가능합니다.
스택
반면 스택은 역시 메모리 구조에서 살펴봤듯이 값이 위로 쌓이는 구조입니다.따라서 값을 넣고 뺄 때 ‘후입 선출’ 또는 ‘LIFO (Last in First Out)’라는 방식을 따르게 됩니다. 가장 나중에 들어온 값이 가장 먼저 나가는 것이죠.
뷔페에서 접시를 쌓아 뒀을 때 사람들이 가장 위에 있는(즉, 가장 나중에 쌓인) 접시를 가장 먼저 들고 가는 것과 동일합니다. 역시 배열이나 연결 리스트를 통해 구현 가능합니다.
딕셔너리
딕셔너리는 ‘키’와 ‘값’이라는 요소로 이루어져 있습니다.
‘키’에 해당하는 ‘값’을 저장하고 읽어오는 것이죠. 마치 대학교에서 ‘학번’에 따라서 ‘학생’이 결정되는 것과 동일합니다. 일반적인 의미에서 ‘해시 테이블’과 동일한 개념이라고도 볼 수 있습니다. 딕셔너리 역시 ‘키’를 어떻게 정의할 것인지가 중요합니다.

