복잡도
알고리즘의 성능을 나타내는 척도
시간 복잡도
특정 크기 입력에 대해 알고리즘의 수행 시간 분석
공간 복잡도
특정 크기 입력에 대해 알고리즘의 메모리 사용량 분석
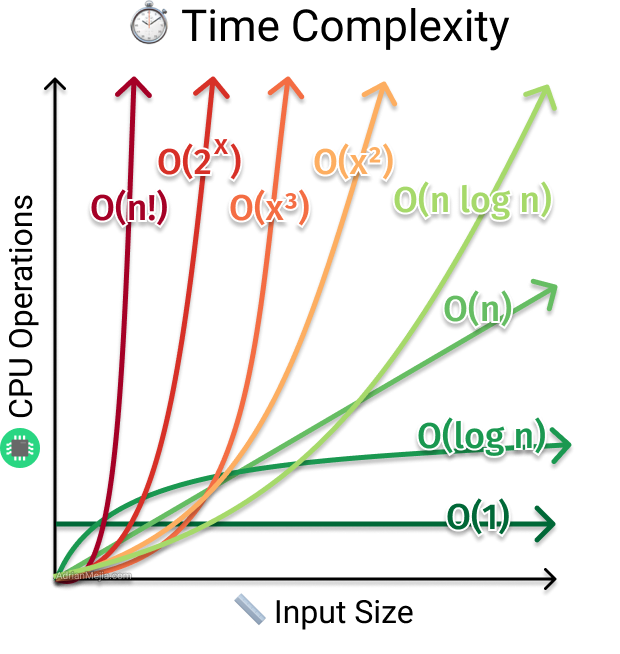
빅오 표기법 (Big-O Notation)
알고리즘의 성능을 표기하는 방법으로 가장 빠르게 증가하는 항을 고려하는 표기법
(x³)
정렬
병합 정렬(Merge Sort)
- 원소의 개수가 1 또는 0이 될때까지 두 부분으로 계속 쪼갠다.
- 쪼개진 원소들을 합치면서 정렬한다.
- 연결 리스트로 구성 시 링크 인덱스만 변경 되기 때문에 데이터 이동이 적어진다.
public class Merge_Sort {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
// 배열 입력 파트
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
int idx = st.countTokens();
int[] arr = new int[idx];
for(int i=0; i<idx;i++){
arr[i] = Integer.parseInt(st.nextToken());
}
mergeSort(arr, 0, arr.length-1);
for(int i=0; i<idx; i++){
System.out.print(arr[i] + " ");
}
}
// 분할
public static void mergeSort(int[] arr, int left, int right){
if (left < right) {
int mid = (left + right) / 2;
mergeSort(arr, left, mid);
mergeSort(arr, mid + 1, right);
merge(arr, left, mid, right);
}
}
// 정렬하면서 합치기
public static void merge(int[] arr, int left, int mid, int right){
int[] temp = new int[arr.length];
int i = left;
int j = mid + 1;
int k = left;
System.out.println("[merge] " + left + " " + mid + " " + right);
System.out.println("[merge] " + "i : " + i + " ,j : " + j + " ,k : " + k);
// 좌분할의 첫 원소와 우분할의 첫 원소를 비교해서 둘 중 더 작은 원소를 temp에 넣는다.
// 넣고 난 후 다음 원소와 큰 원소를 다시 비교한다.
while (i <= mid && j <= right) {
if (arr[i] <= arr[j]) {
temp[k] = arr[i];
i++;
} else {
temp[k] = arr[j];
j++;
}
k++;
}
// 분할된 양쪽 배열 중 남은 배열의 원소들을 temp에 차례대로 넣는다.
while (i <= mid) {
temp[k] = arr[i];
i++;
k++;
}
while (j <= right) {
temp[k] = arr[j];
j++;
k++;
}
// 정렬된 temp 배열을 arr로 옮긴다.
for (int idx = left; idx <= right; idx++) {
arr[idx] = temp[idx];
System.out.print(arr[idx] + " ");
}
System.out.println();
}
}
퀵 정렬(Quick Sort)
- 리스트의 한 요소를 PIVOT으로 정한다.
- PIVOT을 기준 작은값은 왼쪽 큰 값은 오른쪽으로 가게 정렬한다.
- 기준된 왼쪽 리스트와 오른쪽 리스트에 대해 같은 방식을 사용한다.
- 부분된 리스트의 길이가 0이나 1이 될 때까지 반복한다.
힙 정렬(Heap Sort)
힙
완전 이진트리의 일종, 우선순위 큐를 위한 자료구조
완전 이진트리 : 왼쪽부터 순서대로 채워진 이진트리
힙 정렬은?
최소 힙트리 혹은 최대 힙트리를 구성한 후 하나씩 요소를 꺼내 배열에 저장하는 방식
최소 힙 트리 : 부모 노드가 자식 노드보다 작거나 같다.
최대 힙 트리 : 부모 노드가 자식 노드보다 크거나 같다
트리 정렬(Tree Sort)
이진 탐색 트리를 구성한 후 중위 순회 방법으로 순회하면서 정렬하는 방법
기수 정렬(Radix Sort)
낮은 자리부터 비교해서 정렬하는 방법
계수 정렬(Counting Sort)
해당 숫자 인덱스를 추가하는 방식으로 정렬하는 방법
Arrays.sort()
평균 O(NlogN) 최악 O(N^2)
Collections.sort()
평균 O(NlogN) 최악 O(NlogN)
메모리를 추가 사용함
삽입, 병합 정렬 사용

