그래프에서 모든 정점을 방문해야 할때 방문하는 방법에 대해서 다룬다.

너비 우선 탐색과 깊이 우선 탐색

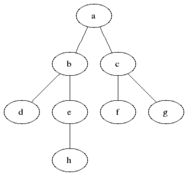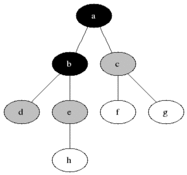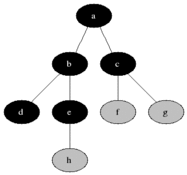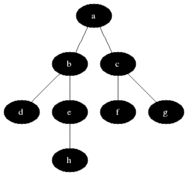
너비 우선 탐색(Breadth-First Search)

현재 위치에서 가까운 곳을 모두 탐색하는 방법

탐색 방법

(1) 시작 정점을 방문한다.
(2) 시작 정점에 인접한 정점을 모두 방문한다.
(3) (2)에서 방문한 정접에 인접한 정점들 중 방문하지 않은 정점들을 방문한다.
(4) 남은 정점이 없을 때까지 반복한다.

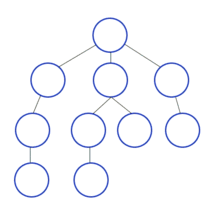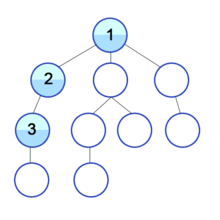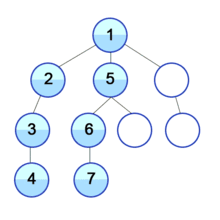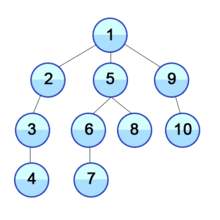
깊이 우선 탐색(Depth-First Search)

현재 위치에서 해당 분기를 완벽하게 탐색하고 다음 분기로 넘어가는 방법
(1) 시작 정점을 방문한다.
(2) 해당 정점에 인접한 정점 하나를 방문한다.
(3) (2)에서 방문한 정점에서 인접한 정점을 방문한다.
(4-1) 인접한 정점이 없을 때까지 반복
(4-2) 인접한 정점이 없을 경우 이전 정점으로 돌아간다.
(5) 남은 정점이 없을 때까지 반복한다.

주의할 점

두 가지 방법 모두 방문한 정점은 방문했다고 체크를 해주어야 루프가 일어나지 않는다.

최소 신장 트리(Minimum Spanning Tree)

신장트리

신장 트리는 그래프 G=(V,E)에서 정점 집합 V를 그대로 두고 간선을 |V|-1만 남겨 트리가 되도록 만든 것이다.

최소 신장 트리

최소 신장트리는 간선이 가중치를 갖는 그래프에서 이런 신장트리들 중 가장 가중치의 합이 작은 트리를 뜻한다.

최소 신장 트리를 찾는 알고리즘

프림 알고리즘

(1) 시작 정점 r의 연결비용을 0, 나머지 정점의 연결 비용을 ∞로 놓는다.
(2) 시작 정점 r을 집합 S에 포함시킨다.
(3) 시작 정점 r에 인접한 정점들의 연결 비용을 가중치로 설정한다.
(4) 집합 S에서 연결할 수 있는 정점들 중 연결 비용이 가장 작은 값인 정점을 집합 S에 포함 시킨다.
(5) 남은 정점이 없을 때까지 반복한다.

크루스칼 알고리즘

간선의 가중치 중 가장 적은 것을 택해 연결되는 정점끼리 집합을 만든다. 단, 사이클이 생기는 간선은 추가하지 않는다