LIS

Longest Increasing Subsequence

최장 증가 부분 수열은 주어진 수열 중에서 증가하는 부분수열 중 가장 긴 수열을 구하는 알고리즘이다.

예시

만약 1 5 2 6 3 7 4 8 9 라는 수열이 있다면
1 5 6 7 8 9
1 2 3 4 8 9 가 LIS에 해당하는 수열이다.

LIS를 구하는 방법

새로운 배열을 선언한다(DP)
DP 배열에는 원소 배열(arr)에서 arr[i]가 마지막일 때 갖는 증가부분수열 중 가장 긴 수열의 길이를 기록한다.

수열을 차례대로 지나면서 해당하는 인덱스의 DP 배열을 확인한다.
1. 첫번째 원소는 계산할 것이 없기 때문에 넣는다.

2. 두번째 원소는 첫번째 원소인 1과 이어질 수 있기 때문에 DP[1]에 1을 더해준다..

3. 세번째 원소, 네번째 원소 역시 첫번째 원소인 1과 이어질 수 있기 때문에 DP[1]에 1을 더해준다.

3. 다섯번째 원소는 비교했을때 Arr[4]에 있는 2와 이어질 수 있기때문에 DP[4]에 1을 더해준다.

4. 이를 반복하며 채우면서 DP 배열을 완성한다.

5. 해당 배열의 LIS 값은 6이다.

• 1 2 3 7 9 10
• 1 2 3 7 8 10

LIS를 구하는 방법 2

위의 방법을 사용할 시에는 앞의 원소들을 전부 확인하며 N개의 수를 확인해야 하기 때문에 O(N^2) 의 시간복잡도를 가진다.

LIS를 구하는 더 빠른 방법은 없을까?

DP 배열의 값을 구하기 위해선 앞에서 이어질 수 있는 원소를 찾아야한다.

• 이때 DP 배열에는 LIS값을 일일히 저장해서 기억했다.
• LIS 값이 가장 큰 arr[N]보다 작은 수를 찾는 과정을 반복했다.
• 이번에는 LIS 값에 해당하는 수 중 가장 작은 수를 DP 배열에 저장한다.

과정

1) Arr 배열을 하나씩 탐색
2) 해당 원소에서 DP 배열의 원소 중 해당 원소보다 작은 값 중 최대값을 찾는다.
3) DP[최대값+1]에 현재 원소를 저장한다.

2) 과정에서 DP 배열은 오름차순으로 저장되기 때문에 이분탐색을 사용할 수 있다 따라서 탐색 과정이 줄어 O(NlogN)의 시간복잡도를 가지게된다.

1. Arr[1]은 LIS가 1이므로 DP[1]에 1을 저장한다.

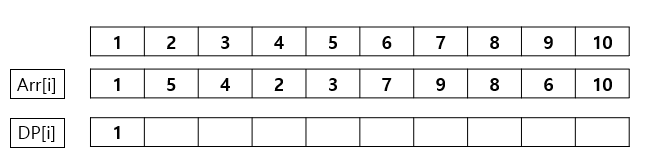
2. Arr[2]는 DP[1]에 저장된 1보다 크기 때문에 LIS가 2이다. 따라서 DP[2]에 Arr[2]인 5를 저장한다.

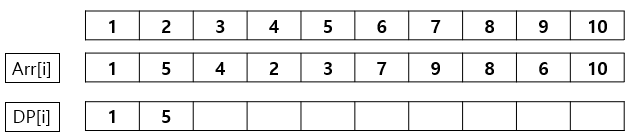
3. Arr[3]은 DP[1]에 저장된 1보다는 크고 DP[2]보다는 작다. 따라서 DP[2]에 Arr[3]을 저장한다.
4. 반복한다.

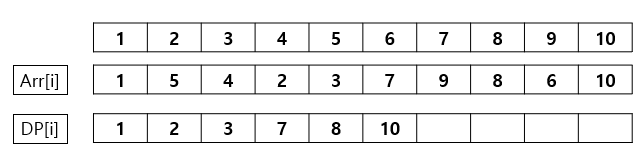
반복하게 될 시 DP 배열은 다음과 같이 채워지게 되며 LIS 값은 값이 채워진 6이 되며 LIS를 구성하는 배열은 DP 배열을 순서대로 출력한 배열이다

알게된 점

코딩테스트 준비 중 알게된 LIS 알고리즘에 대한 정리
정렬된 배열 탐색 -> 무조건 이분탐색!