🎲 이진탐색

배열이 정렬되었다고 가정하고 원하는 요소를 탐색하는 방법.
그냥 냅다 앞뒤로 다 훑는 선형 탐색보다 시간 복잡도가 낮다.

📚 개념

0~6까지의 정수를 담고 있는 배열이 있다고 해보자.
그 중 우리는 1이 어디에 있는지 궁금해졌다.

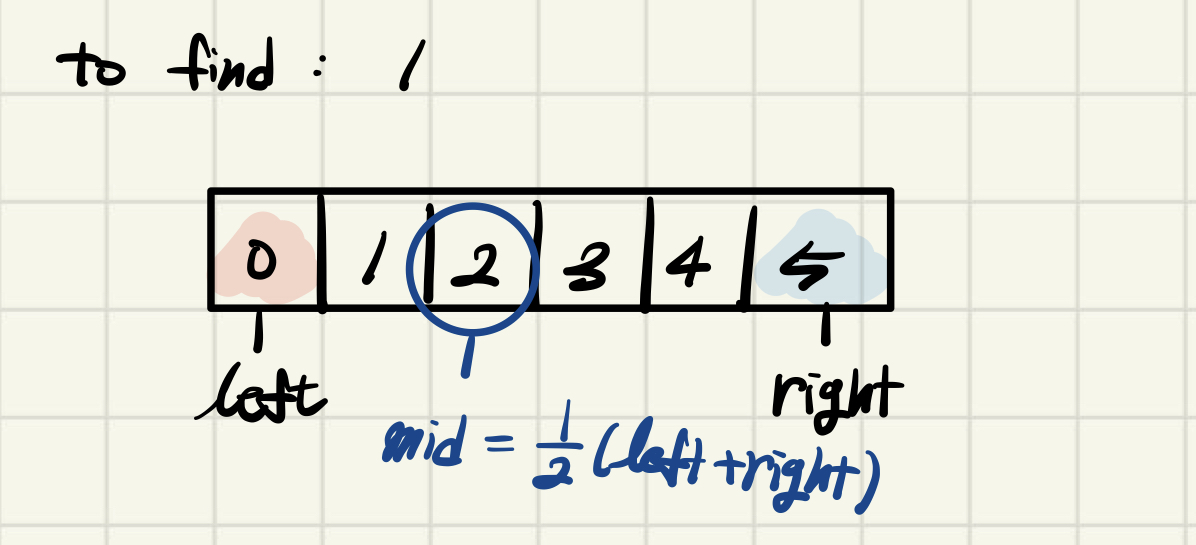
이진 탐색에서는 우선 배열의 양 끝을 더하고 2로 나눔으로써 배열의 중간값 인덱스를 구한다.
그리고 그 중간값과 우리가 찾을 값을 비교하는 것.

위의 사례에서는 중간값이 찾는 값보다 크다.
그러면 배열이 이미 정렬된 상태이므로 우리가 찾는 값은 무조건 중간값보다 왼쪽에 있게 된다.

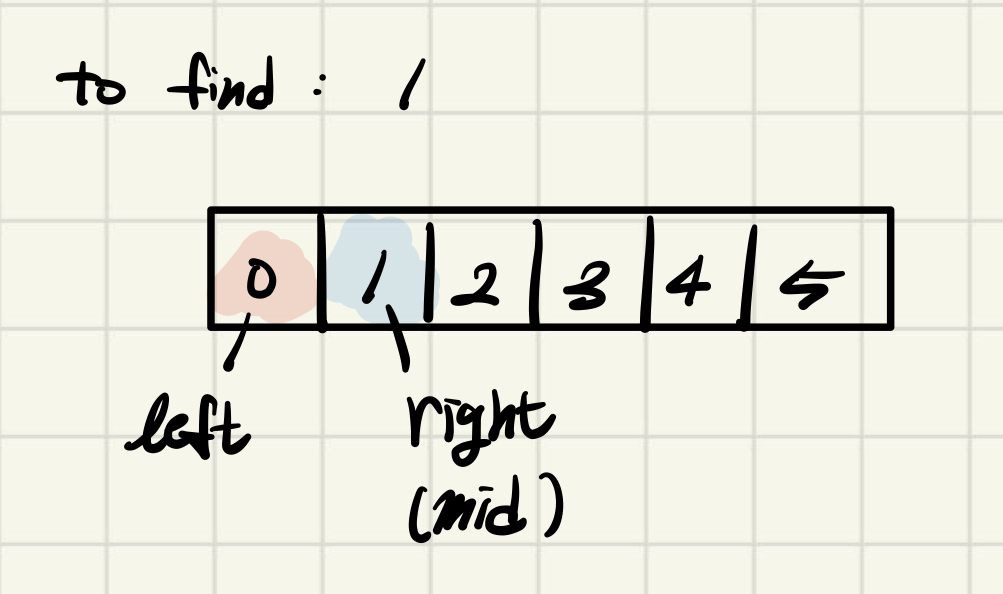
따라서 이렇게 right값을 mid-1 자리로 땡겨옴으로써 범위를 절반씩 좁혀나가는 것이다.
(찾는 값이 중간값보다 클 때는 left값을 mid+1 자리로 땡기게 된다)

위의 사례에서 찾는 값이 0이었다면 left랑 right가 같은 상태가 되어서야 수를 찾을 수 있기 때문에, 조건에 left<=right처럼 등호가 들어가야 한다.

⏰ 시간복잡도

최악의 케이스인 k번 탐색 후 하나를 찾아내는 공식은 다음처럼 된다.

${n(\frac{1}{2})^k}=1$ (단, n=배열 요소의 개수, k=비교 횟수)
식을 정리한다면
${k=\log{n}}$
따라서 시간복잡도는 O(logN)이 된다.

💻 코드

public class binary_search
{
	public static void main(String[] args)
	{
		int[] arr = {1, 2, 3, 4, 5};

		int i = binary(arr, 6);
		System.out.println(i);
	}

	static int binary(int[] arr, int val)
	{
		int left, right, mid;
		
		left = 0;
		right = arr.length-1;

		while (left <= right)
		{
			mid = (left+right)/2;
			if (arr[mid] < val)
				left = mid + 1;
			else if (arr[mid] > val)
				right = mid - 1;
			else
				return mid;
		}
		return -1;
	}
}