안녕하세요!
이번 포스팅에서는 DP, 동적 계획법에 대해서 적어보겠습니다.
동적 계획법
동적 계획법(Dynamic Programming) 은 최적화 문제를 해결하는 알고리즘입니다.
여기서 최적화 알고리즘이란 최대값 또는 최소값을 구하는 문제이거나, 경우의 수를 구하는 문제가 속할 수 있습니다.
동적 계획법은 문제를 작은 문제들로 나누어서 작은 부분 문제들의 해를 구하고, 이것들을 이용해 큰 크기의 부분 문제들을 해결하여 최종 문제를 해결하는 설계 기법입니다.
동적 계획법은 최적 부분문제 구조와 중복 부분문제 구조를 가지고 있어야 한다는 조건이 있습니다.
Optimal substructure
Optimal substructure, 최적 부분문제라고 해석할 수 있는 이것은 어떤 문제에 대한 해가 최적일 때 그 해를 구성하는 작은 문제들의 해 역시 최적이어야 한다는 것입니다.
위에서 동적 계획법은 작은 문제들로 나누어서 먼저 해를 구한 후 그것을 이용해 큰 크기의 부분 문제들을 해결한다고 했습니다.
이 과정에서 애초에 작은 문제가 최적이 아니라면, 그 이후에 구하는 값들도 최적이 아니게 되겠죠.
최적의 원칙이 적용되지 않는 예시는 최장경로 문제가 있습니다.
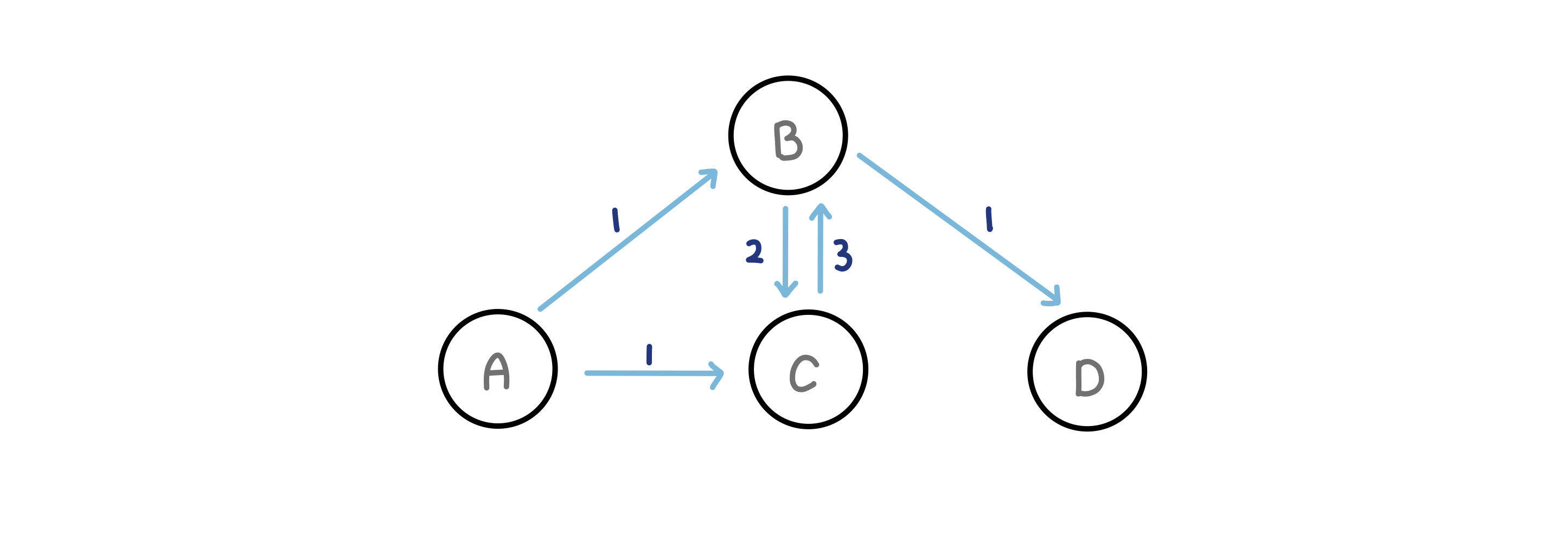
위의 그래프에서 A-D 의 최장 경로는 A-C-B-D 입니다.
하지만 부분 경로인 A-C 의 최장 경로는 A-B-C 가 됩니다.
이 경우에는 최적의 원칙이 적용되지 않기 때문에 DP로 해결할 수 없는 문제라고 할 수 있습니다.
동적 계획법의 로직 자체가 큰 문제의 최적 해를 작은 문제의 최적해들을 이용해 구하기 때문에 이것이 성립하지 않는다면 동적 계획법을 적용할 수 없습니다.
Overlapping subproblems
Overlapping subproblems, 중복 부분문제는 한 번 사용했던 어떤 작은 문제의 해를 다른 어디에서 중복으로 사용될 수 있다는 것을 말합니다.
DP는 큰 문제를 이루는 작은 문제들을 먼저 해결하고 작은 문제들의 최적 해를 이용해 순환적으로 큰 문제를 해결합니다.
이런 순환적인 관계에서 중복이 발생하기 때문에 이미 도출한 작은 문제의 최적해들은 저장 공간에 저장해야 합니다.
이 저장 공간을 DP에서는 동적 테이블이라고 부르며, 흔히 알고 계시는 메모이제이션과 비슷한 원리입니다.
큰 문제의 해를 구할 때 이렇게 저장된 해들이 다시 필요할 때마다 동적 테이블을 참조해 중복 계산을 피합니다.
분할 정복과의 비교
분할 정복과 동적 계획법은 큰 문제를 작은 문제로 나눈다는 것에서 언뜻 비슷해 보입니다.
하지만 두 알고리즘 기법은 확연한 차이가 있습니다.
분할 정복
- 서로 연관 없는 부분 문제로 분할
- 부분 문제를 재귀적으로 해결해 해를 결합한다.
- 하향식 방식으로 접근 (대 -> 소)
- ex) 병합 정렬, 퀵 정렬 ...
DP
- 부분 문제들이 연관이 없으면 적용 불가
- 부분 문제들은 더 작은 부분 문제들을 공유(중복 사용)
- 모든 부분 문제들은 한번만 계산하며 결과를 저장해 계속 재사용
- 상향식 방식으로 접근 (소 -> 대)
피보나치 DP로 풀기
피보나치 문제는 정말 극단적으로 해가 중복되는 문제입니다.
따라서 재귀로 풀게 되면, 메모이제이션을 사용해도 메소드 호출 스택에 메소드가 계속 호출됩니다.
이것은 DP를 활용해 상향식으로 문제를 풀이하면, 시/공간적으로 아주 효율적인 알고리즘이 됩니다.
피보나치의 해를 저장할 배열을 만들고, 0 값과 1 값을 미리 저장해둡니다.
이 값들은 재귀로 구현했을 때는 기저조건이 될 것입니다.
그 후에 for문을 2부터 N까지 순회하면서 점화식 F[i] = F[i-2] + F[i-1] 을 수행합니다.
반복문을 순회한 후 F[N] 을 return하면 끝입니다.
소스 코드
long fibonacci(int N) {
long[] D = new long[N+1];
D[0] = 0;
D[1] = 1;
for (int i = 2; i <= N; ++i) {
D[i] = D[i-2] + D[i-1];
}
return D[N];
}동전 거스름돈 DP로 풀기
1 , 4 , 6 원의 동전이 있습니다.
이 문제에서 9원을 거슬러줘야할 때의 경우의 수는 세 가지가 있습니다.
- 8원에 대한 최적해 + 1원
- 5원에 대한 최적해 + 4원
- 3원에 대한 최적해 + 6원
그렇다면 8원을 거슬러줘야할 때의 경우의 수는 아래와 같을 것입니다.
- 7원에 대한 최적해 + 1원
- 4원에 대한 최적해 + 4원
- 2원에 대한 최적해 + 6원
...
상향식으로 접근했을 때, 현재 구해야 하는 n 이 1보다 크다면 1원을 선택했을 때의 최적해를 계산하고, 4보다 크다면 4원을 선택했을 때의 최적해를 계산하고, 6보다 크다면 6원을 선택했을 때의 최적해를 계산해 세 가지의 경우의 수 중에서 최소를 선택하는 것이 n의 최적해가 될 것입니다.
여기에서 미리 배열에 넣어둬야할 값은 1이 될 것입니다. 1은 무조건 동전 1개만 선택하는 경우의 수만 가능하기 때문입니다. 따라서 반복문은 2 부터 N 까지 순회하는 알고리즘이 도출될 것입니다.
소스 코드
int coin(int N) {
int[] D = new int[N+1];
D[1] = 1;
for (int i = 2; i <= N; ++i) {
int min = Integer.MAX_VALUE;
if (i > 1 && D[i-1] + 1 < min) min = D[i-1] + 1;
if (i > 4 && D[i-4] + 1 < min) min = D[i-4] + 1;
if (i > 6 && D[i-6] + 1 < min) min = D[i-6] + 1;
D[i] = min;
}
return D[N];
}이항 계수 DP로 풀기
이항 계수는 n개에서 k개를 고르는 조합의 가짓수인 nCk를 구하는 것입니다.
(x+y)^3 식에서 x^2y 의 계수 값은 무엇일까요?
이 수식을 풀어쓰면 아래와 같습니다.
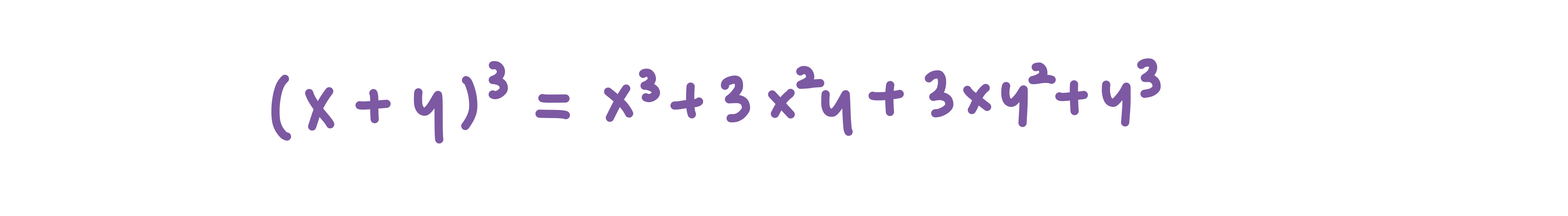
이 식을 조합을 이용해서 더 풀어쓴다면 아래와 같습니다.
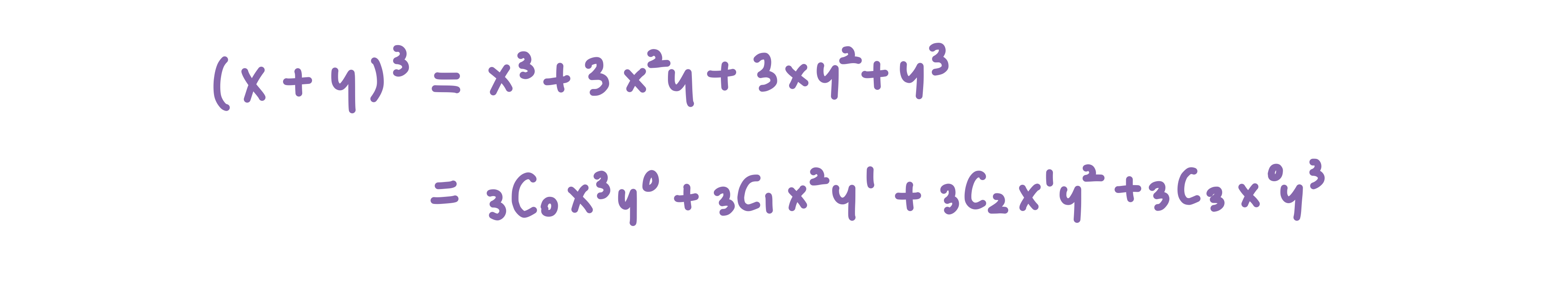
그렇다면 위의 x^2y 의 계수 값을 3C2 또는 3C1 로 볼 수 있을 것입니다.
이것을 점화식으로 일반화한다면 nCk = (n-1)C(k-1) + (n-1)C(k) 가 됩니다.
이항 계수를 동적 계획법으로 쉽게 구현한다면 위의 문제들과는 다르게 이차원 배열을 사용하면 될 것입니다.
동적 계획법에서 기본적으로 처리해야할 코드는, nCk 중 n==k 이거나 k==0 인 경우는 무조건 값이 1 이므로 따로 처리만 해준다면, 점화식 자체는 어렵지 않습니다.
소스 코드
int bino(int N, int K) {
int[][] D = new int[N+1][K+1];
for (int i = 0; i <= N; ++i) {
for (int j = 0; j <= Math.min(i,k); ++j) {
if (j == 0 || j == i) D[i][j] = 1;
else D[i][j] = D[i-1][j-1] + D[i-1][j];
}
}
return D[N][K];
}마무리
0/1 Knapsack 문제는 정리하지 못했는데, 배열을 다양하게 사용한 예제를 다음 포스팅에 담도록 하겠습니다!
이번 포스팅도 읽어주셔서 감사합니다 :)

