[TIL] Tree, BFS, DFS

기면지·2021년 8월 11일

TIL

목록 보기

6/10

안녕하세요!
(어제 공부한 내용이지만) 오늘 쓰니까 아무튼 TIL!!
이번 포스팅에서는 트리와 트리 탐색에 자주 쓰이는 BFS , DFS 를 정리해보겠습니다.

Tree

트리 자료구조는 부모-자식의 1:N 관계를 가지는 비선형 자료구조입니다.
원소들 간에 계층 관계를 가지는 계층형 자료구조라고도 합니다.
상위 원소에서 하위 원소로 내려가면서 확장되는 트리모양의 구조입니다.

용어

노드(node) : 트리의 원소
루트 노드(root node) : 트리의 시작 노드인 최상위 노드
간선(edge) : 노드와 노드를 연결하는 선으로 부모 노드와 자식 노드를 연결
형제 노드(sibling node) : 같은 부모 노드의 자식 노드들
조상 노드 : 간선을 따라 루트 노드까지 이르는 경로에 있는 모든 노드들
서브 트리(subtree) : 부모 노드와 연결된 간선을 끊었을 때 생성되는 트리
자손 노드 : 서브 트리에 있는 하위 레벨의 노드들
차수(degree)
- 노드의 차수 : 노드에 연결된 자식 노드의 수
- 트리의 차수 : 트리에 있는 노드의 차수 중에서 가장 큰 값
- 단말 노드(leaf node) : 차수가 0인 노드, 자식 노드가 없는 노드
높이
- 노드의 높이 : 루트에서 노드에 이르는 간선의 수. 노드의 레벨.
- 트리의 높이 : 트리에 있는 노드의 높이 중에서 가장 큰 값. 최대 레벨.

이진 트리

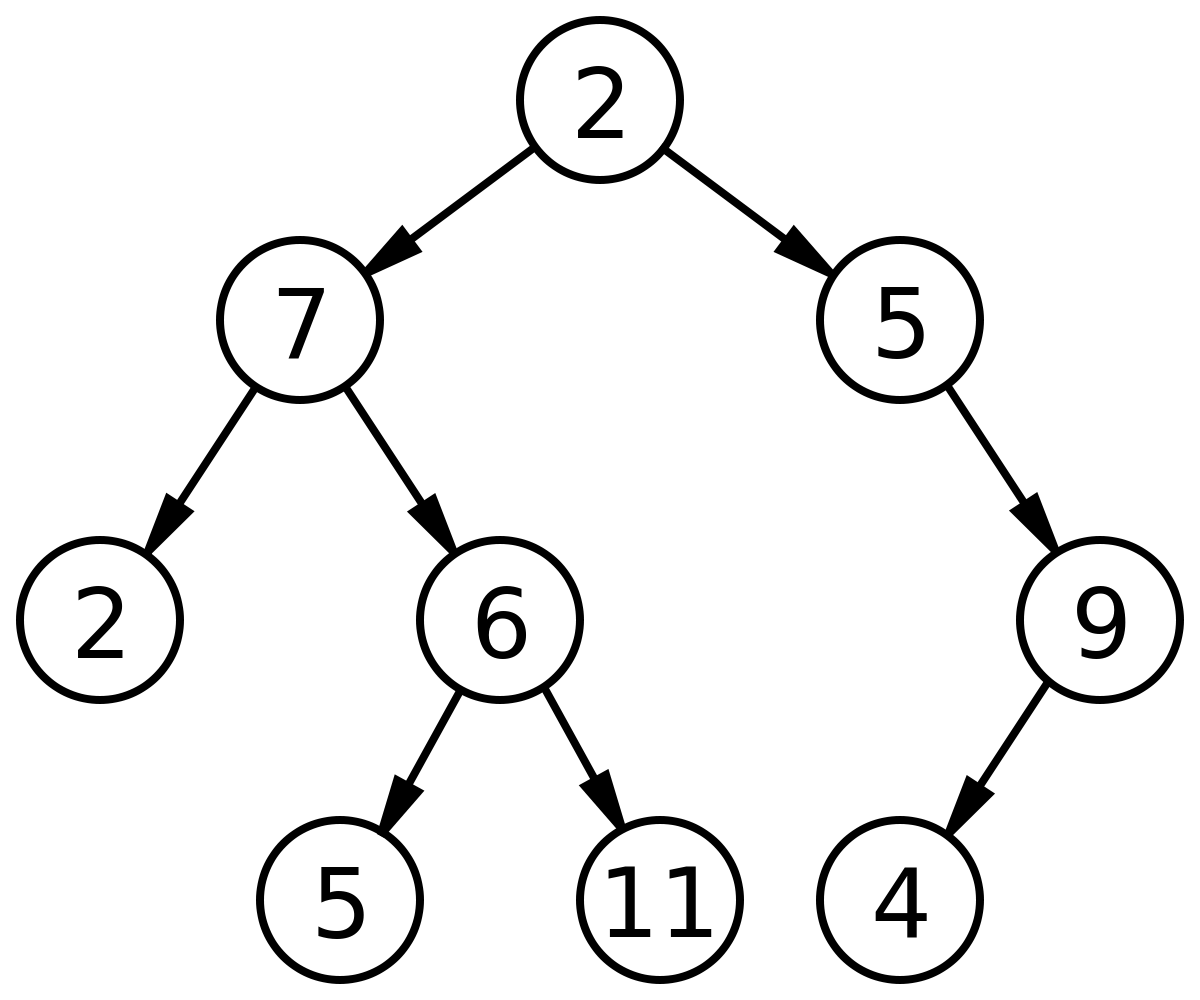
차수가 2인 트리를 이진 트리(Binary tree) 라고 합니다.
각 노드가 자식 노드를 최대 2개만 가질 수 있으며 왼쪽 자식 노드와 오른쪽 자식 노드로 구분합니다.
모든 노드들이 최대 2개의 서브트리를 갖는 특별한 형태의 트리입니다.

이진 트리는 높이(레벨)가 i 인 노드의 최대 개수는 2^i 개 입니다.
높이가 i 인 이진 트리가 가질 수 있는 노드의 최소 개수는 i+1 개, 최대 개수는 2^(i+1)-1) 개 입니다.

포화 이진 트리 (Full Binary Tree)

모든 레벨에 노드가 포화 상태로 차 있는 이진 트리
최대 노드 개수인 2^(i+1)-1 의 노드를 가짐
루트를 1번으로 2^(i+1)-1 까지 정해진 위치에 대한 노드 번호를 가짐

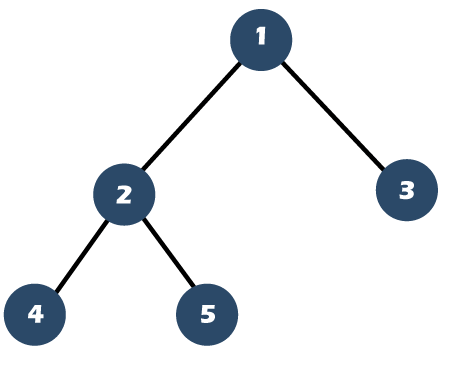
완전 이진 트리 (Complete Binary Tree)

높이가 h 이고 노드 수가 n 개일 때, 포화 이진 트리의 노드 번호 1 번부터 n 번까지 빈 자리가 없는 트리
위의 사진은 노드가 5개인 완전 이진 트리

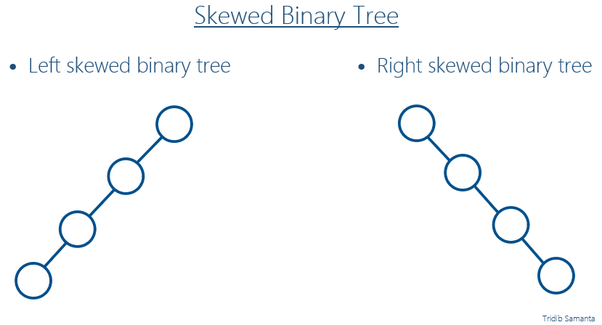
편향 이진 트리 (Skewed Binary Tree)

높이 h 에 대한 최소 개수의 노드를 가지면서 한쪽 방향의 자식 노드만을 가진 트리
왼쪽 편향 이진 트리와 오른쪽 편향 이진 트리가 있음

배열을 이용해 이진 트리 표현

이진 트리에 각 노드 번호를 루트 번호부터 1 로 표현합니다.
레벨 n 에 있는 노드에 대해 왼쪽부터 오른쪽으로 2^n 부터 2^(n+1)-1 까지 번호를 차례로 부여합니다.

번호가 i 인 노드의 부모 노드 번호 : i/2
번호가 i 인 노드의 왼쪽 자식 노드 번호 : 2*i
번호가 i 인 노드의 오른쪽 자식 노드 번호 : 2*i+1
레벨 n 의 노드 번호 시작 : 2^n
높이가 h 인 이진 트리 표현을 위한 배열의 크기 : 2^(h+1)

단점
편향 이진 트리를 배열로 표현할 때 사용하지 않는 배열 원소에 대한 메모리 공간의 낭비가 발생합니다.
또한 트리의 중간에 새로운 노드를 삽입하거나 기존의 노드를 삭제할 경우 배열의 크기 변경이 어려워 비효율적입니다.

코드로 구현하기

public class CompleteBinaryTree {
	
	private char[] nodes;
	private final int SIZE;
	private int lastIndex;	// 마지막 추가된 노드의 인덱스
	
	public CompleteBinaryTree(int size) {
		this.SIZE = size;
		nodes = new char[size+1];
	}
	
	public void add(char c) {
		if (lastIndex == SIZE) return;
		
		nodes[++lastIndex] = c;
	}
}

탐색을 위한 완전 이진 트리의 간단한 기능만 구현합니다.
인덱스는 1부터 시작하고, 마지막으로 추가된 인덱스를 가리키는 lastIndex 멤버 변수도 선언해줍니다.

너비 우선 탐색 (BFS)

너비 우선 탐색 (BFS, Breadth First Search) 은 루트 노드의 자식 노드들을 먼저 모두 차례로 방문한 후에, 방문했던 자식 노드들을 기준으로 해당 노드의 자식 노드를 차례로 방문하는 방식입니다.
인접한 노드들에 대해 탐색 후, 차례로 다시 너비 우선 탐색을 진행해야 하므로, 선입선출 형태의 자료구조인 큐를 활용합니다.

BFS()
	큐 생성
    루트 큐에 삽입
    while(큐가 비어있지 않은 경우) {
    	t <- 큐의 첫 번째 원소 반환
        t 방문
        for (t와 연결된 모든 간선에 대해) {
        	u <- t의 자식 노드
            u를 큐에 삽입
        }
    }
end BFS()

수도 코드로는 위와 같이 나타낼 수 있습니다.

코드로 구현하기

public void bfs() {
    Queue<Integer> queue = new LinkedList<>();
    queue.offer(1);

    int current = 0, level = 0, size = 0;
    while (!queue.isEmpty()) {
        size = queue.size();

        while(--size >= 0) {
            current = queue.poll();

            // 왼쪽 자식이 있다면
            if (current*2 <= lastIndex) queue.offer(current*2);
            // 오른쪽 자식이 있다면
            if (current*2+1 <= lastIndex) queue.offer(current*2+1);
        }
        ++level;
    }
}

CompleteBinaryTree 클래스 안에 bfs() 메소드를 구현했습니다.
노드들을 저장할 queue 를 만들어줍니다.
큐는 노드의 인덱스로 관리할 것이므로 Integer 타입으로 만들었습니다.
루트 노드 인덱스인 1 을 큐에 넣고 시작합니다.

큐가 비지 않을 때까지 while 문을 순회하면서 탐색합니다.
현재 큐의 사이즈를 줄여가면서 current 노드를 구합니다.
current*2 는 자신의 왼쪽 자식의 인덱스를 말하는데, 그것이 마지막으로 큐에 삽입된 lastIndex 보다 작거나 같다면 왼쪽 자식이 존재하는 것이므로 큐에 추가합니다.
current*2+1 은 오른쪽 자식의 인덱스를 말하고, 위와 동일한 로직으로 판단해 큐에 삽입합니다.

그 후에 추후 콘솔에 프린트해보기 위해 level 변수를 증가시킵니다.

public static void main(String[] args) {
    int size = 9;
    CompleteBinaryTree tree = new CompleteBinaryTree(size);

    for (int i = 0; i < size; i++) {
        tree.add((char)(65+i));
    }

    tree.bfs2();
}

테스팅을 위해 메인 메소드에 코드를 작성하고 실행시켜봅니다.

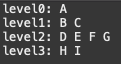
잘 동작하는 것을 확인할 수 있습니다. :)

깊이 우선 탐색 (DFS)

깊이 우선 탐색 (DFS, Depth First Search) 은 루트 노드에서 출발해 한 방향으로 갈 수 있는 경로까지 깊게 탐색하다가 더 이상 갈 곳이 없으면 (단말 노드라면) 가장 마지막에 만났던 갈림길 간선이 있는 노드로 되돌아와서 다른 방향의 노드로 탐색을 계속 반복하여 결국 모든 노드를 방문하는 순회 방법입니다.
가장 마지막에 만났던 갈림길의 노드로 되돌아가서 다시 깊이 우선 탐색을 반복해야 하므로 재귀적으로 구현하거나 후입선출 구조의 스택을 사용해서 구현합니다.

DFS(v)
	v 방문
    for(v의 모든 자식노드 w) {
    	DFS(w)
    }
end DFS()

수도 코드로는 위와 같이 나타낼 수 있습니다.

순회

트리의 순회 (traversal) 는 트리의 노드들을 체계적으로 방문하는 것을 말합니다.
기본적인 순회 방법은 전위순회 , 중위순회 , 후위순회 가 있습니다.

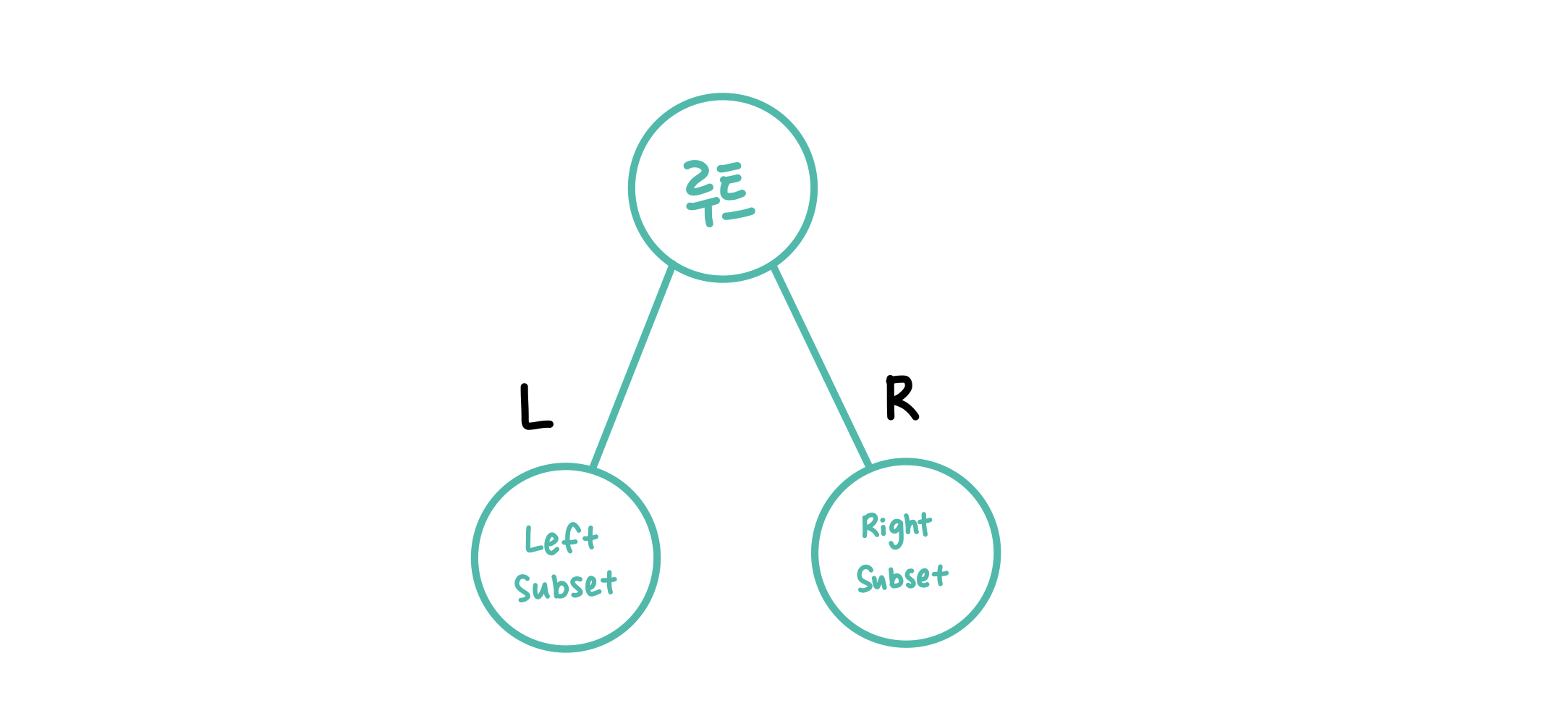
전위순회 (preorder) : 루트LR 부모 노드 방문 후, 자식 노드를 좌-우 순서로 방문
중위순회 (inorder) : L루트R 왼쪽 자식 노드, 부모 노드, 오른쪽 자식 노드 순으로 방문
후위순회 (postorder) : LR루트 자식 노드를 좌-우 순서로 방문한 후 부모 노드를 방문

코드로 구현하기

// 전위순회
public void dfsByPreOrder() {
    System.out.print("Preorder: ");
    dfsByPreOrder(1);
    System.out.println();
}

private void dfsByPreOrder(int current) {
    // 현재 노드 처리
    System.out.print(nodes[current] + " ");
    // 왼쪽 자식 노드 방문
    if (current*2 <= lastIndex) dfsByPreOrder(current*2);
    // 오른쪽 자식 노드 방문
    if (current*2+1 <= lastIndex) dfsByPreOrder(current*2+1);
}

전위 순회 코드를 CompleteBinaryTree 클래스 안에 dfsByPreOrder() 메소드를 오버로딩해서 구현했습니다.
테스팅에서 시작 노드의 인덱스를 바로 매개변수로 전달할 경우 오류가 발생할 가능성이 있기 때문에, 오버로딩해주었습니다.

굉장히 간단한 코드로 구현되었습니다.
현재 노드를 처리하고, dfsByPreOrder() 메소드를 자식 노드를 매개변수로 재귀 호출하면서 구현했습니다.

위 코드를 테스팅한 결과는 아래와 같습니다.

잘 동작하는 것을 확인할 수 있습니다.

나머지 중위순회와 후위순회는 전위순회에서 방문 순서만 변경하면 로직이 완성됩니다.

// 중위순회
private void dfsByInOrder(int current) {
    // 왼쪽 자식 노드 방문
    if (current*2 <= lastIndex) dfsByInOrder(current*2);
    // 현재 노드 처리
    System.out.print(nodes[current] + " ");
    // 오른쪽 자식 노드 방문
    if (current*2+1 <= lastIndex) dfsByInOrder(current*2+1);
}

// 후위순회
private void dfsByPostOrder(int current) {
    // 왼쪽 자식 노드 방문
    if (current*2 <= lastIndex) dfsByPostOrder(current*2);
    // 오른쪽 자식 노드 방문
    if (current*2+1 <= lastIndex) dfsByPostOrder(current*2+1);
    // 현재 노드 처리
    System.out.print(nodes[current] + " ");
}