경사하강법 개념
경사하강법은 비용함수의 값을 최소화하기 위해서 매개변수를 조정해나가는 최적화 알고리즘
경사하강법 알고리즘
경사하강법은 각 반복마다 기울기를 계산해 매개변수를 업데이트하는 방식으로 진행
이 과정에서 기울기는 현재 매개변수 위치에서의 변화율을 의미하고
기울기가 가리키는 방향으로 매개변수를 조정하여 손실을 줄여나가는 것이 핵심
학습률 (Learning rate)
매개변수를 얼마나 빠르게 업데이트할지 결정하는 값
너무 크면 최솟값을 놓칠 수있고, 너무 작으면 학습 속도가 느릴 수도 있다
반복 횟수
경사하강법은 여러 번의 반복을 통해 손실을 줄여나가는데,
이때 충분한 반복이 필요하지만, 너무 많은 반복은 시간 낭비가 될 수 있다
경사하강법과 편미분의 관계
경사하강법에서는 다변수 함수의 최솟값을 찾기 위해 편미분을 사용한다
즉, 각각의 변수에 대해 기울기(변화율)를 계산하고,
기울기를 바탕으로 매개변수를 조정해나가는 방식
경사하강법 계산 예시
1. 데이터 셋
이 데이터는 y=3x+3에 따라 생성된 데이터이다
2. 초기 매개변수 설정
3. 손실 함수 계산 (평균 제곱 오차,MSE)
손실 함수는 예측값 y`=ax + b와 실제값 y 사이의 오차를 계산하는데,
이 오차를 제곱하여 더한 후, 그 평균을 구한다
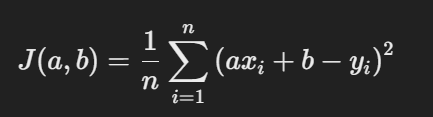
이때에 기울기와 절편을 조정해 최솟값에 도달하는 것이 목표이다
4. 경사하강법을 통한 매개변수 업데이트
각 반복에서 기울기와 절편은 손실 함수의 편미분 값을 사용해 업데이트된다
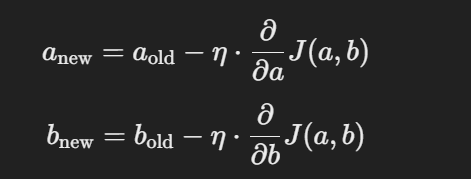
여기서 n은 학습률이다
각각의 편미분을 통해 각각의 매개변수가 손실함수에 얼마나 영향을 미치는지 계산하고
이에 따라 매개변수의 값을 조정한다
5. 반복 및 수렴
이 과정을 계속 반복해서 더 이상 값이 크게 변하지 않거나 오차가 최소화되는 지점까지 진행
Shine like a star, Just like a star