미래값을 예측해보자

1. 문제

Amazon 시계열 데이터 (792개 시점)을 가지고 미래값을 예측해볼 것이다

핵심 아이디어
복잡한 시계열을 단순한 성분들로 분해할 것이고
각 성분의 패턴을 LSTM에 학습시킬 것이다
그리고 그 학습시킨 것으로 미래를 예측해볼 것이다

그렇다면 왜 분해는 하는걸까?
원본 데이터는 너무 복잡해서 패턴을 찾기가 어렵고
또 트렌드, 계절성, 노이즈가 섞여있다 하지만
분해를 하면 각각의 패턴을 명확하게 볼 수 있다
그래서 우리는 분해를 할 것이다

원본 = 트렌드 + 계절성 + 노이즈
-> 트렌드만 따로, 계절성만 따로 학습하면 더 쉽다

2. 데이터 확인

일단 데이터를 확인해보자

import numpy as np
import matplotlib.pyplot as plt

amazon_data = np.loadtxt('amazon.txt')

# 데이터 기본 통계
print("Amazon 데이터 분석:")
print(f"데이터 길이 : {len(amazon_data)}")
print(f"평균 : {np.mean(amazon_data):.2f}")
print(f"표준편차 : {np.std(amazon_data):.2f}")
print(f"최솟값 : {np.min(amazon_data)}")
print(f"최대값 : {np.max(amazon_data)}")

# 시각화 
plt.figure(figsize = (12,6))
plt.plot(amazon_data)
plt.title('Amazon Time Series data')
plt.xlabel('time')
plt.ylabel('value')
plt.show()

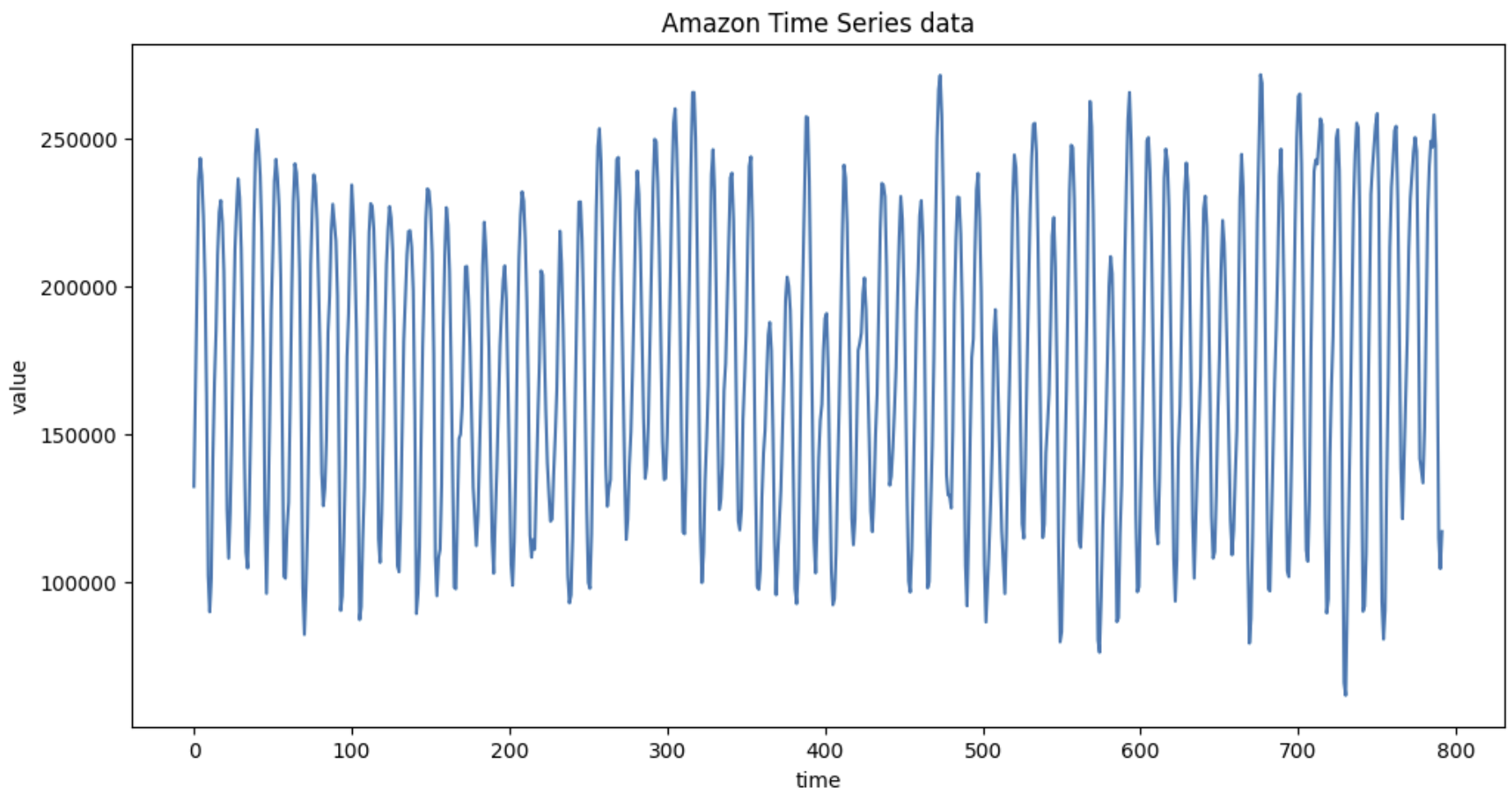
데이터를 확인해보면 전체적으로 큰 변동성을 가졌고,
주기적인 오르내림을 가지고 있으며 불규칙한 변동이 있어보인다

3. Fourier 분석

Fourier 분석이란?

모든 복잡한 신호는 여러 개의 단순한 사인파의 합으로 표현할 수 있다

예시를 들어보면
아름다운 음악 = 도 + 미 + 솔 ... (각각 다른 주파수)
복잡한 주식 = 장기 트렌드 + 월별 패턴 + 주간 패턴 + ...
이런식으로 나눌 수 있다는 것이다

Fourier 분석 과정
1. 데이터에서 주기적인 패턴 찾기
2. 각 주기의 강도(파워) 계산
3. 가장 강한 4개의 주기 선택
4. 이 4개로 원본 신호 근사

수학적 배경
성분(t) = a × cos(2πt/T) + b × sin(2πt/T)
T = 주기 (period)
a = 코사인 계수 (cosine coefficient)
b = 사인 계수 (sine coefficient)
t = 시간 인덱스

최적 계수 찾기
a = Σ[신호(t) × cos(2πt/T)] / (N/2)
b = Σ[신호(t) × sin(2πt/T)] / (N/2)

원본 신호와 cos/sin 파형의 내적을 계산해서 가장 비슷한 패턴을 찾는다

# Fourier 성분 생성 함수
def create_fourier_component(signal, period):
    N = len(signal)

    # 최적의 사인/코사인 계수 찾기
    a_sum = 0 # 코사인 계수
    b_sum = 0 # 사인 계수 
    
    # 계수 계산 루프
    for t in range(N):
        angle = 2 * np.pi * t / period
        a_sum += signal[t] * np.cos(angle)
        b_sum += signal[t] * np.sin(angle)
    ## 각 시점에서 원본 신호와 cos/sin 값을 곱해서 누적한다 
    ## 이는 원본 신호가 해당 주기의 cos/sin 성분을 얼마나 포함하는지를 측정하는 과정

    # 계수 정규화
    a = 2* a_sum  / N
    b = 2* b_sum / N
     
    # 성분 생성
    component =[]
    for t in range(N):
        angle = 2 * np.pi  * t / period
        value = a * np.cos(angle)  + b * np.sin(angle)
        component.append(value)
    ## 계산된 계수를 사용해서 해당 주기의 Fourier 성분을 생성한다 
    
    return component
    
# 4개의 주요 성분 생성 
periods = [12,24,36,48]
fourier_components = [] 

for period in periods:
    component = create_fourier_component(amazon_data, period)
    fourier_components.append(component)
    print(f"주기 {period} 성분 생성 완료")

정리를 하면 복잡한 시계열에서 특정 주기의 패턴을 찾기 위해서
그 주기의 사인파와 코사인파로 원본 신호를 가장 잘 근사하는 계수를 찾고
원본 신호의 해당 주기 성분만 분리해서 추출을 했다

4. 잔차 계산

잔차(Residual)란?

잔차 = 원본 - 예측된 부분

우리의 경우에는
R = S - (성분1 + 성분2 + 성분3 + 성분4)

잔차가 중요한 이유는 4개 성분이 설명하지 못한 부분을 설명해주고
모델의 한계를 보여준다 이 잔차는 작으면 작을수록 좋다

작은 잔차 : 4개의 성분이 원본을 잘 설명
큰 잔차 : 아직 설명 못한 패턴이 많음

# 잔차 계산
# 4개의 성분의 합 
fourier_sum = np.zeros(len(amazon_data)) # 0으로 초기화

for component in fourier_components :
    fourier_sum += component # 각 성분을 누적해서 더하기

# 잔차 = 원본 - 성분들의 합 
R_fourier = amazon_data - fourier_sum

# 시각화 
plt.figure(figsize =(12,5))
plt.subplot(2,1,1)
plt.plot(amazon_data , label="Original")
plt.plot(fourier_sum, label="The sum of the four components")
plt.legend()
plt.title ("original vs reconstitution")

plt.subplot(2,1,2)
plt.plot(R_fourier, 'r-')
plt.title('Residual (unexplained)')
plt.show()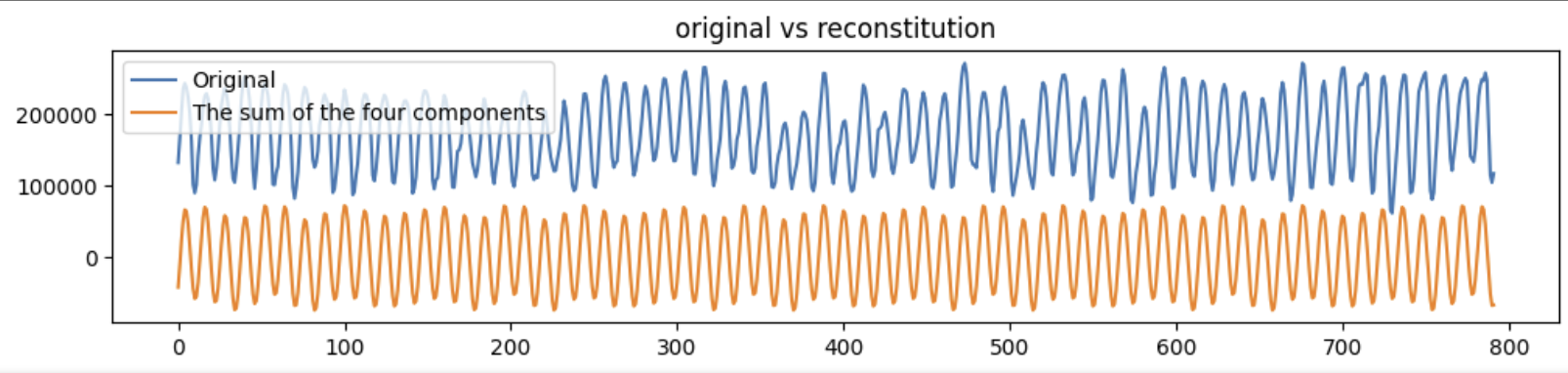

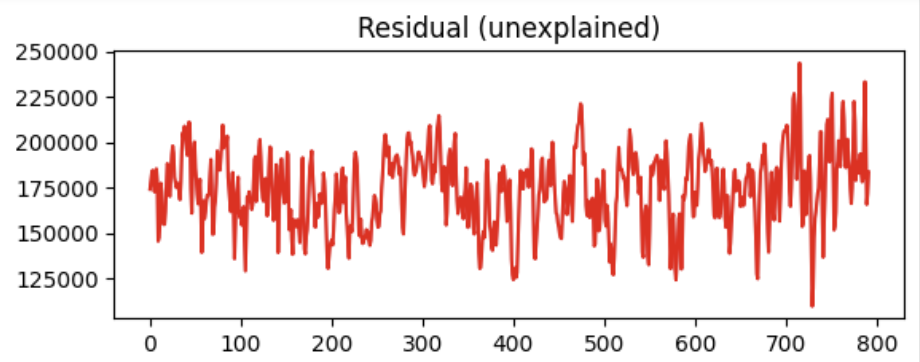
분산으로 분해 품질 측정

분산 = 데이터가 얼마나 퍼져있는지
Var(X) = Σ(X - 평균)² / N

원본 분산 : 원본 데이터의 총 변동성
잔차 분산 : 설명하지 못한 변동성

설명된 분산 비율 : (1-잔차분산/원본분산) * 100%

100%로 가까울수록 완벽한 분해
80% 이상이면 쓸만하고 50% 미만이면 분해 방법에 문제가 있다는 것을 의미한다

# 분해 품질 평가
original_var = np.var(amazon_data)
residual_var = np.var(R_fourier)
explained_var = (1 - residual_var/original_var) * 100

print(f"원본 분산: {original_var:.2f}")
print(f"잔차 분산: {residual_var:.2f}")
print(f"설명된 분산: {explained_var:.1f}%")

5. 행렬 만들기

LSTM에 입력할 데이터를 만들어보자

크기 : 792 x 5
5개의 특징 : (4개의 성분 + 1개 잔차)

각 행의 의미는
B[0] = [성분1[0], 성분2[0], 성분3[0], 성분4[0], 잔차[0]]
B[1] = [성분1[1], 성분2[1], 성분3[1], 성분4[1], 잔차[1]]
...

이렇게 구성을 하면 각 시점에서 모든 성분의 값을 동시에 보여주고
LSTM이 5차원 정보를 학습할 수 있다

# B 행렬 구성
B_fourier = np.zeros((len(amazon_data), 5)) 
## 792개 행(시점) x 5개 열(특징)을 담을 빈 컨테이너 준비

# 각 열에 성분 배치
B_fourier[:, 0] = fourier_components[0]  # 성분 1
B_fourier[:, 1] = fourier_components[1]  # 성분 2
B_fourier[:, 2] = fourier_components[2]  # 성분 3  
B_fourier[:, 3] = fourier_components[3]  # 성분 4
B_fourier[:, 4] = R_fourier             # 잔차
## 각 열에 해당 주기의 패턴을 저장
## 4개의 성분이 설명하지 못한 나머지 정보는 잔차에 저장 


print(f"B 행렬 크기: {B_fourier.shape}")
print(f"첫 번째 시점의 특징: {B_fourier[0]}")

# 각 특징의 통계
for i in range(5):
    name = f"성분{i+1}" if i < 4 else "잔차"
    print(f"{name}: 평균={np.mean(B_fourier[:, i]):.2f}, "
          f"표준편차={np.std(B_fourier[:, i]):.2f}")

문제가 발생했다!! 결과값을 보면 이상하고 이상하다
잔차: 평균=173,976.63, 표준편차=20,214.95

이는 잔차 평균이 원본 평균(174,124)과 거의 같다
이는 4개 Fourier 성분이 아무것도 설명을 하지 못했다는 의미이고
모든 중요한 정보가 잔차에 몰려있다는 뜻이다
그러면 LSTM은 자연스럽게 잔차에만 의존하게 될 거다

원인은 Fourier 변환은 기본적으로 AC(변동) 성분만 추출하고
DC(직류, 평균) 성분은 별도 처리가 필요하기 때문이다

그래서 해결책으로 원본데이터에서 평균(DC)를 미리 제거하고
중심화된 데이터로 Fourier 분해를 수행하고
DC 성분을 마지막에 따로 추가하여 각 성분이 순수한 변동만 담도록 할 것이다

1) 평균제거 (중심화)

중심화는 원본 데이터에서 평균을 빼는 과정을 이야기한다
centered_data = original_data - mean(original_data)

# 평균 제거 후 재분해
amazon_mean = np.mean(amazon_data)
amazon_centered = amazon_data - amazon_mean

Before: Amazon 데이터: 61,870 ~ 271,400 (평균: 174,124)
After: 중심화 데이터: -112,254 ~ 97,275 (평균: 0)
이제 Fourier 변환이 순수한 변동 패턴만 포착한다

2) 중심화된 데이터로 Fourier 분해

이전 분해는 원본 데이터에 DC 성분이 섞여있기에
중심화된 데이터로 새롭게 분해를 해야한다 -> 순수 AC 성분만 나오게 된다

# 중심화된 데이터로 Fourier 분해
fourier_components_fixed = []
for period in [12, 24, 36, 48] :
    # 중심화된 데이터로 분해 
    component = create_fourier_component(amazon_centered, period)
    # 혹시 남은 DC 제거 
    component_centered = component - np.mean(component)
    fourier_components_fixed.append(component_centered)

왜 component - np.mean(component)를 또 할까?

그 이유는 Fourier 변환의 수치적 한계 때문이다
이론적으로는 AC 성분의 평균은 0이지만 부동소수점 오차로 미세한 DC가 남는다
그렇기에 완벽한 중심화를 위해 추가 보정이 필요하다

이러한 행동을 우리는 이중 중심화라고 한다

3) 순수 잔차 계산

# 순수 잔차 계산
fourier_sum_fixed = np.sum(fourier_components_fixed, axis=0)
R_fourier_fixed = amazon_centered - fourier_sum_fixed

이전 방식
R = 원본 - (4개 성분의 합) -> 잔차에 DC 성분이 모두 몰림

새로운 방식
R = 중심화 데이터 - (4개 순수 AC 성분의 합) -> 순수한 변동

4) 행렬 다시 구성

# 수정된 B 행렬
B_fourier_fixed = np.zeros((len(amazon_data), 5))
B_fourier_fixed[:, 0] = fourier_components_fixed[0]
B_fourier_fixed[:, 1] = fourier_components_fixed[1]
B_fourier_fixed[:, 2] = fourier_components_fixed[2]
B_fourier_fixed[:, 3] = fourier_components_fixed[3]
B_fourier_fixed[:, 4] = amazon_mean + R_fourier_fixed  # DC + 순수잔차

열 0~3은 순수 AC 성분들이 있고, 열 4에는 DC와 순수잔차가 있다
이를 통해서 AC들의 합 + 평균 + 순수잔차로 완벽한 복원을 할 수 있다

print("=== DC 성분 수정 전 ===")
print(f"잔차 평균: {np.mean(R_fourier):.2f}")

print("\n=== DC 성분 수정 후 ===")
for i in range(5):
    name = f"성분{i+1}" if i < 4 else "DC+잔차"
    mean_val = np.mean(B_fourier_fixed[:, i])
    std_val = np.std(B_fourier_fixed[:, i])
    print(f"{name}: 평균={mean_val:.2f}, 표준편차={std_val:.2f}")

# 재구성 검증
reconstruction = np.sum(B_fourier_fixed, axis=1)
error = np.mean((amazon_data - reconstruction)**2)
print(f"재구성 오차: {error:.12f}")

# 최종 B 행렬로 교체
B_fourier = B_fourier_fixed

6) 입력과 타겟 설정

# 입력과 타겟 설정
x = B_fourier[:-1] # 첫 791개 시점 (입력)  마지막 행을 제외한 모든 행 = B_fourier[0:791]
y = amazon_data[1:] # 뒤 791개 시점 (타겟) 첫 번째 값을 제외한 모든 값  = amazon_data[1:792]

print(f"입력 x 크기 :{x.shape}") # 입력 x 크기 :(791, 5)
print(f"출력 y 크기 :{len(y)}") # 출력 y 크기 :791

이제 시계열 예측에 사용할 입력과 출력을 설정을 해보자
일단 입력(x)는 크기는 (791,5)로 시점 t의 5차원 특징이다
출력(y)는 크기(791,)로 시점 t+1의 원본 값을 의미한다

그냥 쉽게 말하면 시점 0의 5차원의 특징을보고 시점 1의 원본값을 예측하는 것이다
그렇게 총 791개의 (입력, 타겟) 학습 샘플이 만들어졌다

하지만 치명적인 논리적 문제가 있다

1. 차원 불일치 : 5차원 -> 1차원 예측 ???
2. 분해 -재구성 모순 : 분해된 성분으로 원본을 예측
3. 시간 윈도우 부재 : 한 시점만으로 예측하기에 LSTM 장점을 못살린다

그래도 일단은 진행을 해보자

7. 데이터 분할

시계열 데이터는 그냥 분할을 하면 큰일난다
왜냐하면 시간 순서가 매우 중요하기 때문이다

• Train : 과거 데이터 (시점 0~473)
• Val : 중간 데이터 (시점 474~631)
• Test : 미래 데이터 (시점 632~790)

이렇게 6:2:2 비율로 진행을 했다
60%는 훈련데이터, 20%는 하이퍼파라미터 튜닝용
나머지 20%는 평가용데이터이다

# 6:2:2 분할
n = len(x) 
train_size = int(0.6*n) # 474
val_size = int(0.2*n) # 158
test_size = n - train_size - val_size # 159

# 시간 순서대로 분할
x_train = x[:train_size]
y_train = y[:train_size]

x_val = x[train_size : train_size + val_size]
y_val = y[train_size : train_size + val_size]

x_test = x[train_size + val_size :]
y_test = y[train_size + val_size :]

print(f"데이터 분할 결과")
print(f"Train : {len(x_train)}개 ({len(x_train)/n*100:.1f}%)")
print(f"Val : {len(x_val)}개 ({len(x_val)/n*100:.1f}%)")
print(f"Test : {len(x_test)}개 ({len(x_test)/n*100:.1f}%)")

# 시간 범위 확인
print(f"\nTrain 시점 : 0 ~ {train_size -1}")
print(f"Val 시점 : {train_size} ~ {train_size + val_size -1}")
print(f"Test 시점 : {train_size + val_size} ~ {n-1}")

8. 데이터 정규화

바로 학습시키전에 데이터 정규화 작업을 해줄거다
LSTM 훈련에서 정규화를 하는 이유는 간단하다

1) 스케일이 불균형하다
성분1: -45,000 ~ 45,000 (범위: 90,000)
성분2: -300 ~ 300 (범위: 600)
DC+잔차: 140,000 ~ 200,000 (범위: 60,000)

2) 학습 불안정
큰 값이 작은 값을 압도함
또 경사도 폭발이나 소실에 문제가 생길 수 있고 수렴 속도가 느려질 수 있다

3) 가중치 편향
LSTM은 큰 스케일 특징에만 집중한다
작은 스케일 특징은 무시한다 그래서 패턴 학습의 실패할 수 있다

그래서 우리는 MinMaxScaler를 통해서
모든 특징이 0~1 범위로 균등화되도록 해줄거다

from sklearn.preprocessing import MinMaxScaler

# MinMaxScaler 생성 및 학습
scaler_x = MinMaxScaler()
scaler_y = MinMaxScaler()

📐 MinMaxScaler 공식
X_scaled = (X - X_min) / (X_max - X_min)
모든 값이 0~1 범위로 변환

이렇게 하면 모든 특징이 동등한 중요도를 가지게 되며
신경망 학습도 안정화가 되며 빠른 수렴을 하게 된다

# Train 데이터로 스케일러 학습
X_train_scaled = scaler_x.fit_transform(x_train)
y_train_scaled = scaler_y.fit_transform(y_train.reshape(-1, 1)).flatten()

# Val, Test 데이터 변환 (Train 스케일러 사용)
X_val_scaled = scaler_x.transform(x_val)
y_val_scaled = scaler_y.transform(y_val.reshape(-1, 1)).flatten()

X_test_scaled = scaler_x.transform(x_test)
y_test_scaled = scaler_y.transform(y_test.reshape(-1, 1)).flatten()

train 데이터로만 스케일러를 학습시킨다
왜나하면 미래 정보가 과거 스케일에 영향을 미치기도 하고,
데이터 누수가 발생할 수 있기 때문이다

그 다음에는 y 데이터를 reshape 해야한다 왜냐하면
원본 y 형태는 1차원 배열인데 MinMaxScaler는 2차원 배열을 요구한다
그래서 (474,) -> (474,1) 로 변환해야 하고 다시 변환해준다
왜냐하면 LSTM 타켓은 1차원이어야 하기에

print("정규화 전 범위:")
print(f"X_train: {x_train.min():.2f} ~ {x_train.max():.2f}")
print(f"y_train: {y_train.min():.2f} ~ {y_train.max():.2f}")

print("\n정규화 후 범위:")
print(f"X_train: {X_train_scaled.min():.3f} ~ {X_train_scaled.max():.3f}")
print(f"y_train: {y_train_scaled.min():.3f} ~ {y_train_scaled.max():.3f}")

9. LSTM

LSTM = Long Short-Term Memory
시계열 데이터의 패턴을 학습하는 신경망으로 장기간의 의존성을 기억할 수 있다

import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import LSTM, Dense, Dropout


# LSTM 모델 구성
def create_lstm_model(units=32,dropout=0.1):
    model = Sequential([
        # 첫 번째 LSTM 층
        LSTM(units, return_sequences=True, input_shape=(1, 5)),
        Dropout(dropout),

        # 두 번째 LSTM 층
        LSTM(units//2, return_sequences=False),
        Dropout(dropout),

        # 완전 연결층
        Dense(25, activation='relu'),
        Dense(1) # 출력층
    ])

    return model

# 모델 생성
model = create_lstm_model(32,0.1)
model.compile(optimizer ='adam', loss='mse', metrics=['mae'])

# 모델 구조 확인
model.summary()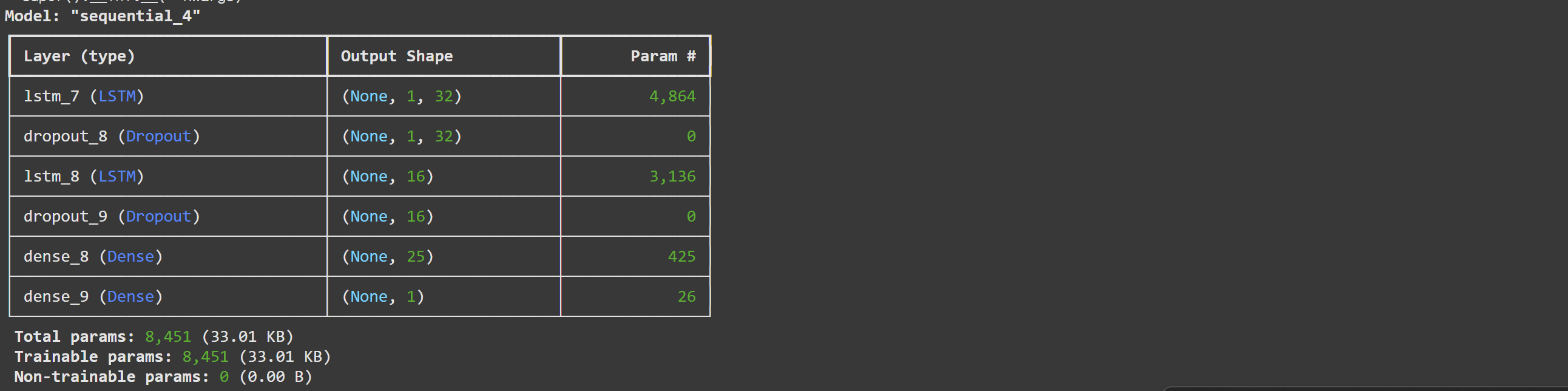

LSTM 모델을 구체적으로 확인을 해보자

첫 번째 LSTM 층
return_sequences=True는 모든 timestep의 출력을 반환하며
다음 LSTM 층으로 시퀀스를 전달한다
형태 : (batch_size, timesteps, units)

input_shape(1,5)
1개의 timestep, 5개의 특징으로 배치 크기는 자동으로 추론한다

units=32
32개의 LSTM 뉴런으로 각 뉴런이 패턴을 학습한다

Dropout 층
Dropout은 과적합을 방지하는 역할을 수행하며 훈련 중에 일부 뉴런을 무작위로
비활성화 하여 모델이 특정 뉴런에 과도하게 의존하지 못하도록 한다
dropout=0.1의 의미는 10%의 뉴런을 무작위로 제거하고
90%의 뉴런만 활성화시킨다는 의미이다 너무 높으면 학습 능력이 저하되고
너무 낮으면 과적합이 될 수 있기에 보통 0.1~0.3 범위로 설정한다

두 번째 LSTM 층
return_sequences=False
마지막 timestep의 출력만 반환한다 시퀀스를 고정 크기 벡터로 압축
형태 : (batch_size, units)

첫 번째 층의 시퀀스 정보를 종합하고 최종 예측을 위한 특징을 추출한다

Dense 층
첫 번째 Dense는 25개의 뉴런이 있고 비선형 패턴 학습을 한다
Relu 활성화 함수를 사용했다

두 번째 Dense는 1개의 뉴런으로 최종 예측값을 출력한다
활성화 함수가 없다 (선형)
회귀문제이므로 실수값을 출력한다

모델 컴파일
optimizer = 'adam'
학습률 자동 조정을 하며 빠르고 안정적으로 학습할 수 있도록 한다

loss= 'mse'
회귀문제의 표준손실함수 = (실제값-예측값)^2 의 평균

metrics=['mae']
추가 성능 지표로 절댓값 기반 오차를 측정해준다

# LSTM 입력 형태로 변환 (samples, timesteps, features)
X_train_lstm = X_train_scaled.reshape(X_train_scaled.shape[0], 1, 5)
X_val_lstm = X_val_scaled.reshape(X_val_scaled.shape[0], 1, 5)
X_test_lstm = X_test_scaled.reshape(X_test_scaled.shape[0], 1, 5)

print(f"LSTM 입력 형태: {X_train_lstm.shape}") # LSTM 입력 형태: (474, 1, 5)

LSTM 입력 요구사항은
(sample, timesteps, feature)로 3차원 배열 필수이다
하지만 현재 데이터는 2차원이기에 변환이 필요했다 -> (474,5) -2차원

그래서 reshape 과정을 통해
timesteps : 한 시점만 사용
features : Fourier 성분 + 잔차
samples : 훈련 샘플 개수
(474, 1, 5) - 3차원

timesteps가 1개인 것은 현재 실험 설계의 한계이다

10. 하이퍼파라미터 튜닝

하이퍼파라미터 튜닝이란 모델의 설정을 최적화하는 과정으로
사람이 직접 설정해야 하는 값들을 이야기한다
이는 모델 성능에 큰 영향을 미친다

from tensorflow.keras.callbacks import EarlyStopping

# 하이퍼파라미터 조합들
hyperparams = [
    {'units': 32, 'dropout': 0.1, 'lr': 0.001, 'batch_size': 16},
    {'units': 50, 'dropout': 0.2, 'lr': 0.001, 'batch_size': 32},
    {'units': 64, 'dropout': 0.2, 'lr': 0.0005, 'batch_size': 16},
    {'units': 40, 'dropout': 0.15, 'lr': 0.0008, 'batch_size': 20},
]

best_val_loss = float('inf') # 무한대로 초기화 
best_params = None # 최적 하이퍼파라미터 저장
best_model = None # 최적 모델 저장

# 반복 실험 
for i, params in enumerate(hyperparams):
    print(f"조합 {i+1}: {params}")
    
    # 모델 생성
    model = create_lstm_model(params['units'], params['dropout'])
    model.compile(optimizer=tf.keras.optimizers.Adam(params['lr']), 
                  loss='mse')
    
    # 조기 종료 설정
    early_stopping = EarlyStopping(monitor='val_loss', patience=15, 
                                   restore_best_weights=True)
    
    # 학습
    history = model.fit(
        X_train_lstm, y_train_scaled,
        validation_data=(X_val_lstm, y_val_scaled),
        epochs=100,
        batch_size=params['batch_size'],
        callbacks=[early_stopping],
        verbose=0
    )
    
    # 최적 모델 선택
    val_loss = min(history.history['val_loss'])
    print(f"검증 손실: {val_loss:.6f}")
    
    if val_loss < best_val_loss:
        best_val_loss = val_loss
        best_params = params
        best_model = model

print(f"\n최적 하이퍼파라미터: {best_params}")

Unit : LSTM 뉴런 개수 (32, 50, 64, 40)
Dropout : 과적합 방지 (0.1,0.2,0.15,0.3)
Learning Rate : 학습 속도 (0.001,0.0005,0.0008)
Batch Size : 한 번에 처리할 데이터 (16, 20, 24, 24, 32)

그렇게 구한 최적의 파라미터는 다음과 같다
{'units': 40, 'dropout': 0.15, 'lr': 0.0008, 'batch_size': 20}

# 최종 예측
y_pred_scaled = best_model.predict(X_test_lstm, verbose=0)

# 역정규화
y_pred = scaler_y.inverse_transform(y_pred_scaled).flatten()

# RMSE 계산
from sklearn.metrics import mean_squared_error
rmse = np.sqrt(mean_squared_error(y_test, y_pred))

print(f"최종 테스트 RMSE: {rmse:.2f}")

# 추가 지표들
mae = np.mean(np.abs(y_test - y_pred))
mape = np.mean(np.abs((y_test - y_pred) / y_test)) * 100

print(f"MAE: {mae:.2f}")
print(f"MAPE: {mape:.2f}%")

먼저 하이퍼파라미터 튜닝에서 선택된 최적 모델을 사용해서
학습에 사용되지 않은 새로운 테스트 데이터로 최종 예측을 수행했다
그리고 역정규화로 원래 스케일로 되돌렸다

RMSE (Root Mean Square Error)
RMSE = √(Σ(실제값 - 예측값)² / 데이터 개수)
• 예측값과 실제값의 차이를 측정
• 낮을수록 좋음
• 원본 데이터와 같은 단위

추가적으로
MAE는 평균 절대 오차로 평균적으로 예측이 실제값에서 얼마나 벗어나는가를
MAPE는 평균 절대 백분율 오차로 평균적으로 몇 %의 오차가 발생했는지를 알려준다

좀 더 시각화해서 알아보자

# 예측 결과 시각화
plt.figure(figsize=(12, 6))
plt.plot(y_test[:50], 'b-', label='Real value', linewidth=2)
plt.plot(y_pred[:50], 'r--', label='Expected value', linewidth=2)
plt.title(f' (RMSE: {rmse:.2f})')
plt.xlabel('time')
plt.ylabel('valuse')
plt.legend()
plt.grid(True)
plt.show()

# 예측 오차 분석
errors = y_test - y_pred
plt.figure(figsize=(12, 4))
plt.hist(errors, bins=30, alpha=0.7)
plt.title('Prediction Error Distribution')
plt.xlabel('Error')
plt.ylabel('Frequency')
plt.show()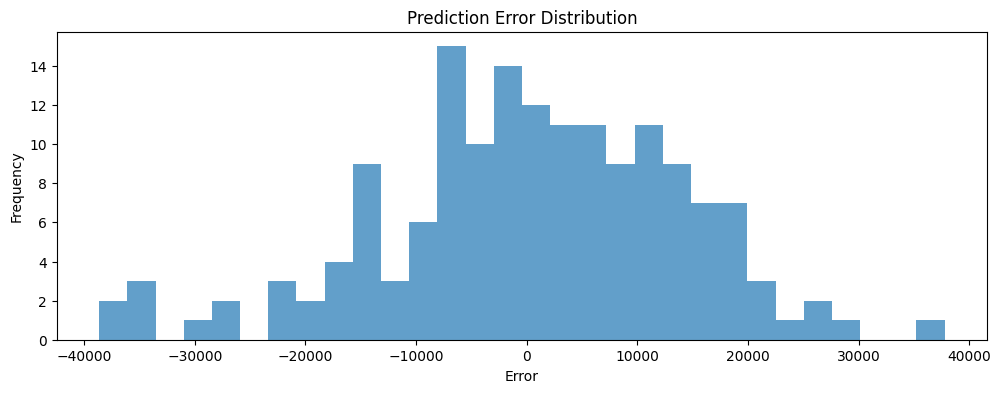

11. SSA + LSTM

이제까지는 Fourier 분석으로 주기적 패턴을 추출했다면
이번에는 SSA 방식으로 사용해보자

SSA는 시계열을 여러 개의 주성분으로 분해하는 방법으로
주파수 기반이 아닌 특이값 분해(SVD)를 사용한다
트랜드, 주기성, 노이즈를 자동으로 분리할 수 있다

Fourier: 주파수 도메인, 고정된 주기 패턴에 특화
SSA : 시간 도메인, 비정상 시계열과 복잡한 패턴 처리 가능

SSA 과정
임베딩: 시계열을 궤적 행렬로 변환
SVD 분해: 특이값 분해로 주성분 추출
그룹핑: 상위 4개 고유값에 대응하는 성분 선택
대각선 평균화: 성분을 다시 시계열로 변환

def ssa_decomposition(time_series, window_length=None, n_components=4):
    """
    SSA를 사용하여 가장 큰 고유값 4개에 대응하는 signal 추출
    """
    N = len(time_series)
    if window_length is None:
        window_length = N // 4  # 전체 길이의 1/4
    
    L = window_length  # 윈도우 길이
    K = N - L + 1      # 궤적 행렬의 열 개수
    
    print(f"SSA 파라미터: N={N}, L={L}, K={K}")
    
    # 1단계: 임베딩 - 궤적 행렬 X 구성
    X = np.zeros((L, K))
    for i in range(K):
        X[:, i] = time_series[i:i+L]
    
    # 2단계: SVD 분해
    U, sigma, Vt = np.linalg.svd(X, full_matrices=False)
    
    # 고유값은 특이값의 제곱
    eigenvalues = sigma**2
    
    print("상위 4개 고유값:")
    for i in range(n_components):
        ratio = eigenvalues[i] / np.sum(eigenvalues) * 100
        print(f"  성분 {i+1}: {eigenvalues[i]:.2e} ({ratio:.1f}%)")
    
    # 3단계: 상위 4개 성분 재구성
    components = []
    
    for i in range(n_components):
        # i번째 성분의 재구성 행렬
        Xi = sigma[i] * np.outer(U[:, i], Vt[i, :])
        
        # 4단계: 대각선 평균화
        reconstructed_component = diagonal_averaging(Xi, N)
        components.append(reconstructed_component)
    
    return components, eigenvalues[:n_components]

def diagonal_averaging(Xi, N):
    """대각선 평균화를 통해 시계열로 변환"""
    L, K = Xi.shape
    reconstructed = np.zeros(N)
    
    for k in range(N):
        diagonal_elements = []
        for i in range(L):
            j = k - i
            if 0 <= j < K:
                diagonal_elements.append(Xi[i, j])
        
        if diagonal_elements:
            reconstructed[k] = np.mean(diagonal_elements)
    
    return reconstructed

# SSA 분해 수행
print("\n=== SSA 분해 ===")
ssa_components, ssa_eigenvalues = ssa_decomposition(amazon_data, n_components=4)

# 잔차 계산: R = S - (4개 signal의 합)
ssa_sum = np.sum(ssa_components, axis=0)
R_ssa = amazon_data - ssa_sum

print(f"SSA 재구성 오차: {np.mean((amazon_data - ssa_sum)**2):.2e}")

# SSA 분해 품질 평가
ssa_explained_var = (1 - np.var(R_ssa) / np.var(amazon_data)) * 100
print(f"SSA 설명 분산: {ssa_explained_var:.1f}%")

# Fourier vs SSA 비교
print("\n=== 분해 방법 비교 ===")
print(f"Fourier 설명 분산: {explained_var:.1f}%")
print(f"SSA 설명 분산: {ssa_explained_var:.1f}%")

# SSA B 행렬 구성 (792, 5)
B_ssa = np.zeros((len(amazon_data), 5))
B_ssa[:, 0] = ssa_components[0]  # 성분 1
B_ssa[:, 1] = ssa_components[1]  # 성분 2  
B_ssa[:, 2] = ssa_components[2]  # 성분 3
B_ssa[:, 3] = ssa_components[3]  # 성분 4
B_ssa[:, 4] = R_ssa             # 잔차

print(f"SSA B 행렬 크기: {B_ssa.shape}")

# 입력/타겟 설정 (Fourier와 동일한 방식)
x_ssa = B_ssa[:-1]  # 입력
y_ssa = amazon_data[1:]  # 타겟 (동일)

# 데이터 분할 (동일한 비율로)
x_ssa_train = x_ssa[:train_size]
x_ssa_val = x_ssa[train_size:train_size + val_size]  
x_ssa_test = x_ssa[train_size + val_size:]

# 정규화
scaler_x_ssa = MinMaxScaler()
X_ssa_train_scaled = scaler_x_ssa.fit_transform(x_ssa_train)
X_ssa_val_scaled = scaler_x_ssa.transform(x_ssa_val)
X_ssa_test_scaled = scaler_x_ssa.transform(x_ssa_test)

# LSTM 형태로 변환
X_ssa_train_lstm = X_ssa_train_scaled.reshape(X_ssa_train_scaled.shape[0], 1, 5)
X_ssa_val_lstm = X_ssa_val_scaled.reshape(X_ssa_val_scaled.shape[0], 1, 5)
X_ssa_test_lstm = X_ssa_test_scaled.reshape(X_ssa_test_scaled.shape[0], 1, 5)

print("\n=== SSA LSTM 하이퍼파라미터 튜닝 ===")

# 동일한 하이퍼파라미터 조합으로 공정한 비교
best_val_loss_ssa = float('inf')
best_params_ssa = None
best_model_ssa = None

for i, params in enumerate(hyperparams):
    print(f"SSA 조합 {i+1}: {params}")
    
    # 모델 생성 (동일한 구조)
    model = create_lstm_model(params['units'], params['dropout'])
    model.compile(optimizer=tf.keras.optimizers.Adam(params['lr']), 
                  loss='mse')
    
    # 조기 종료
    early_stopping = EarlyStopping(monitor='val_loss', patience=15, 
                                   restore_best_weights=True)
    
    # 학습
    history = model.fit(
        X_ssa_train_lstm, y_train_scaled,  # y는 동일
        validation_data=(X_ssa_val_lstm, y_val_scaled),
        epochs=100,
        batch_size=params['batch_size'],
        callbacks=[early_stopping],
        verbose=0
    )
    
    val_loss = min(history.history['val_loss'])
    print(f"검증 손실: {val_loss:.6f}")
    
    if val_loss < best_val_loss_ssa:
        best_val_loss_ssa = val_loss
        best_params_ssa = params
        best_model_ssa = model

print(f"\nSSA 최적 하이퍼파라미터: {best_params_ssa}")

12. Fourier vs SSA

# SSA 최종 예측
y_pred_ssa_scaled = best_model_ssa.predict(X_ssa_test_lstm, verbose=0)
y_pred_ssa = scaler_y.inverse_transform(y_pred_ssa_scaled).flatten()

# SSA 성능 지표
rmse_ssa = np.sqrt(mean_squared_error(y_test, y_pred_ssa))
mae_ssa = np.mean(np.abs(y_test - y_pred_ssa))
mape_ssa = np.mean(np.abs((y_test - y_pred_ssa) / y_test)) * 100

print("=== 최종 성능 비교 ===")
print(f"{'방법':<10} {'RMSE':<10} {'MAE':<10} {'MAPE':<10}")
print("-" * 40)
print(f"{'Fourier':<10} {rmse:.2f}     {mae:.2f}     {mape:.2f}%")
print(f"{'SSA':<10} {rmse_ssa:.2f}     {mae_ssa:.2f}     {mape_ssa:.2f}%")

# 승자 결정
if rmse_ssa < rmse:
    winner = "SSA"
    improvement = rmse - rmse_ssa
else:
    winner = "Fourier"
    improvement = rmse_ssa - rmse

print(f"\n🏆 승자: {winner}")
print(f"성능 차이: {improvement:.2f} RMSE")

실험 1 (Fourier + LSTM): RMSE = 13768.54
실험 2 (SSA + LSTM): RMSE = 31116.34

최적 하이퍼파라미터:
Fourier: {'units': 40, 'dropout': 0.15, 'lr': 0.0008, 'batch_size': 20}
SSA: {'units': 32, 'dropout': 0.1, 'lr': 0.001, 'batch_size': 16}

분해 품질:
Fourier 설명 분산: 83.6%
SSA 설명 분산: 87.3%

✨ Fourier 방법이 더 우수한 성능을 보였다

13. 정리

🏆 주요 발견사항
1. Fourier 분해가 SSA보다 17347.80 낮은 RMSE 달성
2. 주기적 패턴이 강한 아마존 주식 데이터에 Fourier가 더 적합

🔍 방법론별 특성 분석
Fourier Analysis :
✅ 장점: 명확한 주파수 해석, 계산 효율성
❌ 단점: 비정상성 처리 한계, 고정 주기 가정

SSA :
✅ 장점: 비정상 시계열 처리, 적응적 패턴 추출
❌ 단점: 높은 계산 복잡도, 윈도우 길이 민감성

🔍 한계점
1. 시간 윈도우 제약: 현재 timestep=1로 LSTM의 장점 미활용
2. 단일 데이터셋: 다양한 시계열에 대한 일반화 검증 필요
3. 기본 LSTM 구조: 더 발전된 아키텍처 적용 가능
4. 정적 윈도우: SSA의 윈도우 길이 적응적 조정 필요

🛠️ 개선방안
1. 다중 시점 입력: sequence length 확장
2. 교차 검증: 시계열 특성 고려한 검증 방법
3. 앙상블 모델: 여러 분해 방법의 조합
4. 하이퍼파라미터 자동 최적화: Bayesian Optimization 적용

현재 -> 다중 시점으로 변환한다는 것은 다음과 같이 바꾸는 것을 의미한다

# 현재: 한 시점만 보고 예측
X[0] = [comp1[0], comp2[0], comp3[0], comp4[0], residual[0]]  → y[1] 예측
X[1] = [comp1[1], comp2[1], comp3[1], comp4[1], residual[1]]  → y[2] 예측
>
# 개선: 10개 시점을 보고 예측
X[0] = [[comp1[0:10], comp2[0:10], comp3[0:10], comp4[0:10], residual[0:10]]]  → y[10] 예측
X[1] = [[comp1[1:11], comp2[1:11], comp3[1:11], comp4[1:11], residual[1:11]]]  → y[11] 예측

이렇게 바꿔서 사용을 하면 timesteps=1에서 10으로 적용을 할 수 있어서
LSTM의 성능을 더 잘 사용할 수가 있다

코드는 대략적으로 비슷해서 이번에는 다 서술하지 않고 결과만 가져오겠다

RMSE는 낮을수록 좋은 지표이므로, 시퀀스 방식이 오히려 성능을 악화시켰다
그 이유는 데이터가 부족해서 그럴 것이다
왜냐하면 길이 10이 되면서 데이터가 적어졌기 때문이다
우리는 이를 통해서 또 시퀀스 확장이 항상 좋은 것은 아니다라는 사실을 알 수 있었다

"더 복잡한 모델 ≠ 더 좋은 성능"
"데이터와 문제에 맞는 적절한 복잡도가 중요"