그리디 알고리즘이란(Greedy Algorithm)?
그리디 알고리즘은 동적 프로그래밍을 간단한 문제 해결에 사용하면 지나치게 많은 일을 한다는 것 때문에 고안되었습니다.
그리디 알고리즘(탐욕법이라고도 한다)이란 현재리디 알고리즘이란 현재 상황에서 가장 좋은 것을 고르는 알고리즘을 말합니다.
그리디 알고리즘은 3가지 단계로 구분할 수 있습니다.
- 선택 절차(Selection Procedure): 현재 상태에서 최적의 해답을 선택한다.
- 적절성 검사(Feasibility Check): 선택된 답이 문제의 조건을 만족하는지 검사한다.
- 해답 검사(Solution Check): 원래의 문제가 해결되었는지 검사하고, 해결되지 않았다면 선택 절차로 돌아가 위의 과정을 반복한다.
즉, 현재 상황에서 최선의 선택을 하는 것을 말합니다.
하지만 그리디 알고리즘을 사용한다고 해서 가장 좋은 결과를 도출해주는 것은 아닙니다.
왜 최선의 선택이 최고의 결과로 이어지지 않는가?
다음과 같은 문제가 있다고 가정해봅시다.
시작지점에서 다음 지점으로 갈 때 최종 지점까지의 합이 가장 큰 수를 구하라.
(이 때 시작지점의 값은 0이다.)
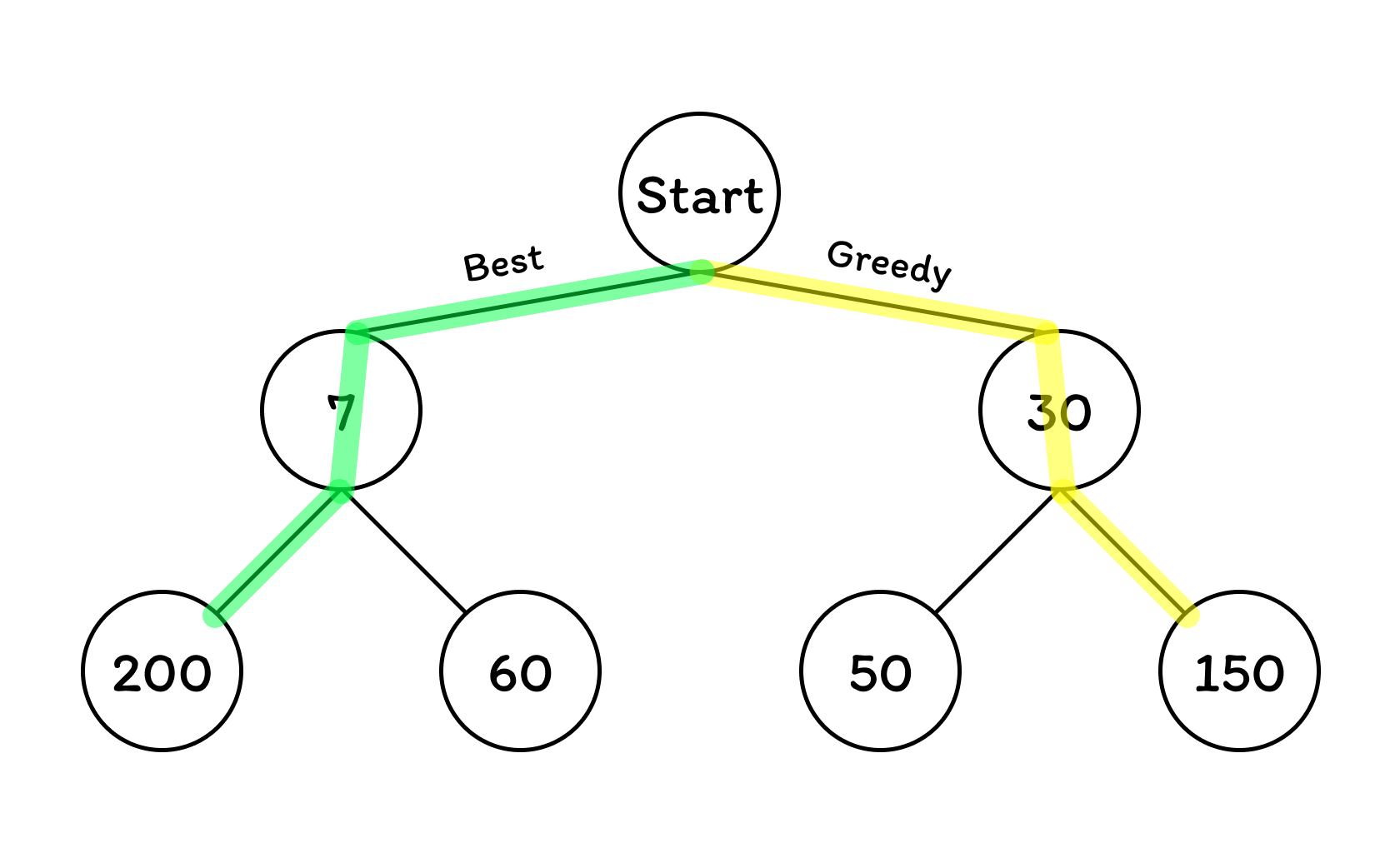
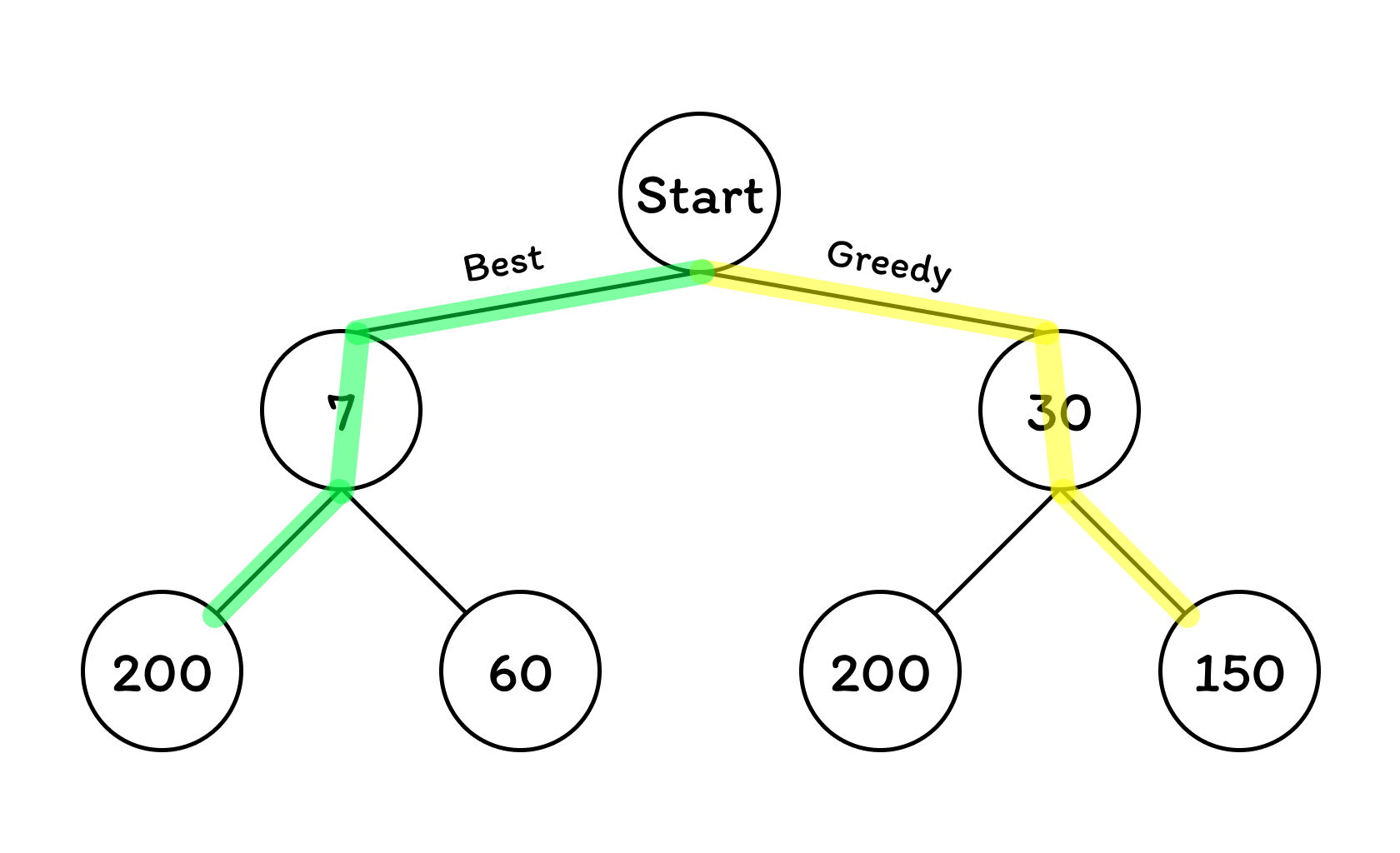
해당 문제를 위 그림대로 그리디 알고리즘으로 푼다면, 항상 최적의 선택을 하기에 Start-30-150으로 180이라는 결과가 나옵니다.
하지만 합이 가장 커야하기 때문에 합까지 고려한다면 Start-7-200으로 가는 경로가 최종 결과값이 207로 가장 크게 됩니다.
그럼 어떤 상황에서 사용할 수 있을까?
그리디 알고리즘을 사용하기 위한 조건으로는 2가지가 있습니다.
- 탐욕스러운 선택 조건
- 탐욕적인 선택은 항상 안전해야 합니다. 다시 말해 최상의 조건만을 선택했을 때 그 결과도 최상이어야 한다는 것입니다.
- 최적 부분 구조 조건
- 1번과 비슷한 의미이기도 합니다. 문제에 대한 최종 해결 방법이 부분 문제에 대해서도 최상의 해결방법이어야 합니다.
또한, 그리디 알고리즘에서 고려하는 상황의 값들이 서로 영향을 주면 안 됩니다.
위 문제에서 그리디 알고리즘이 도출한 최종 경로는 Start-30-150 입니다. 이 경로는 Start-7-200과 구분되어 있어 변경할 수 없습니다.
그리디 알고리즘 문제 예시
그리디 알고리즘을 사용하여 백준 2839번: 설탕배달 해당 문제를 해결할 수 있습니다.
상근이는 요즘 설탕공장에서 설탕을 배달하고 있다. 상근이는 지금 사탕가게에 설탕을 정확하게 N킬로그램을 배달해야 한다. 설탕공장에서 만드는 설탕은 봉지에 담겨져 있다. 봉지는 3킬로그램 봉지와 5킬로그램 봉지가 있다.
상근이는 귀찮기 때문에, 최대한 적은 봉지를 들고 가려고 한다. 예를 들어, 18킬로그램 설탕을 배달해야 할 때, 3킬로그램 봉지 6개를 가져가도 되지만, 5킬로그램 3개와 3킬로그램 1개를 배달하면, 더 적은 개수의 봉지를 배달할 수 있다.
상근이가 설탕을 정확하게 N킬로그램 배달해야 할 때, 봉지 몇 개를 가져가면 되는지 그 수를 구하는 프로그램을 작성하시오.
혹은 백준 5585번: 거스름돈 해당 문제를 해결할 수 있습니다.
타로는 자주 JOI잡화점에서 물건을 산다. JOI잡화점에는 잔돈으로 500엔, 100엔, 50엔, 10엔, 5엔, 1엔이 충분히 있고, 언제나 거스름돈 개수가 가장 적게 잔돈을 준다.
타로가 JOI잡화점에서 물건을 사고 카운터에서 1000엔 지폐를 한장 냈을 때, 받을 잔돈에 포함된 잔돈의 개수를 구하는 프로그램을 작성하시오.
혹은 정렬과 같이 사용하여 [백준 1931번: 회의실 배정] 해당 문제를 해결할 수 있습니다.
한 개의 회의실이 있는데 이를 사용하고자 하는 N개의 회의에 대하여 회의실 사용표를 만들려고 한다. 각 회의 I에 대해 시작시간과 끝나는 시간이 주어져 있고, 각 회의가 겹치지 않게 하면서 회의실을 사용할 수 있는 회의의 최대 개수를 찾아보자.
단, 회의는 한번 시작하면 중간에 중단될 수 없으며 한 회의가 끝나는 것과 동시에 다음 회의가 시작될 수 있다. 회의의 시작시간과 끝나는 시간이 같을 수도 있다. 이 경우에는 시작하자마자 끝나는 것으로 생각하면 된다.
