DFS와 BFS의 란?

트리, 그래프, 탐색 알고리즘에 자주 쓰인다. 이둘을 바이너리 트리에서 구분해보고, 로직을 그래프까지 확장시켜보자

DFS vs BFS

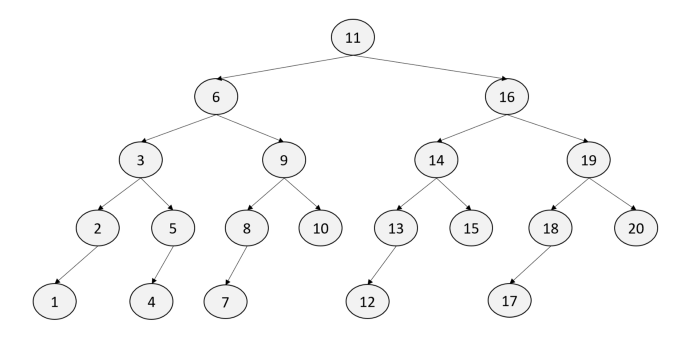
트리를 통해 알아보자

BFS

BFS Breadth First Search로 너비를 우선적으로 탐색한다.

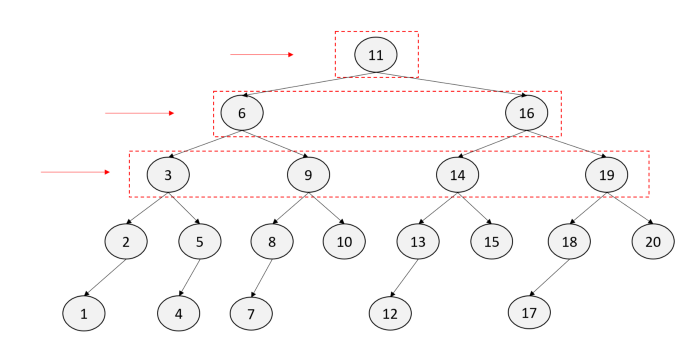
root가 11인 트리는 연결된 자식 노드인 6과 16을 먼저 탐색한다. (11->6-16)
그후 6의 자식 노드와 16의 자식노드를 탐색한다. (3->9->14-16)
BFS를 구현하기 위해 Queue를 사용할 수 있다. 트리의 루트에서 시작하여 큐에서 이미 지난 노드들을 제거하고, 새롭게 탐색해야할 노드들을 추가한다. 예시에서 보자면 11에서 시작해서, 연결된 자식노드들을 큐에 추가해준다. 6과 11일 추가된다. 이러한 진행 방식은 큐의 모든 데이터가 소진될 때까지 진행된다.

def bfs(root):
   bfs_q = deque([root])
   path = []
   while bfs_q:
       for i in range(len(bfs_q)):
           out = bfs_q.popleft()
           path.append(out.val)
           if out.left:
               bfs_q.append(out.left)
           if out.right:
               bfs_q.append(out.right)
   return path

큐의 결과값은 아래와 같다

11           #start
6, 16        #removed 11 and added its connected.
3, 9, 14, 19 #removed 6 and 16 added their connected nodes
2, 5, 8, 10, 13, 15, 18, 20

DFS

DFS는 Depth First Search로 깊이를 우선적으로 탐색한다. 수평적으로 탐색한 bfs와 다르게 수직적으로 탐색을 실시한다. dfs에서는 연결된 노드의 끝까지 탐색을 하고 역행하여 다시 탐색하지 않은 방향으로 다시 탐색하게 된다.

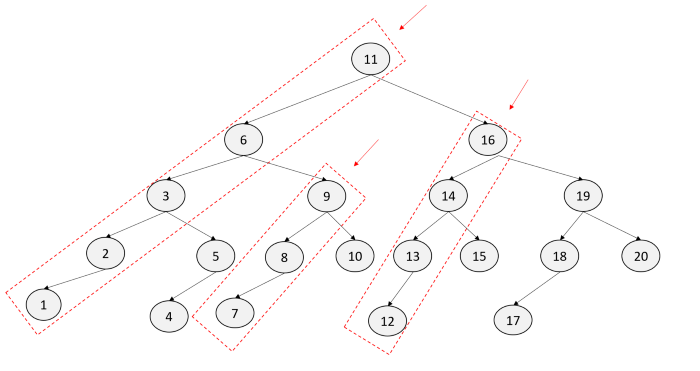
예시를 살펴보면 11->6->3->2->1 역행 9->8->7
DFS를 구현하기 위해 Stack을 사용한다. stack을 사용함으로써 이미 방문한 노드를 체크해둘수 있다. 스택에 유일한 엘레멘트인 루트에서 부터 시작하여, 스택으로 부터 꺼내고 연결된 꺼낸 노드랑 연결된 노드를 추가한다. 모든 스택이 빌 때까지 사용한다.

def dfs(root):
    stack = [root]
    path = []
    while stack:
        out = stack.pop()
        path.append(out.val)
        if out.right:
            stack.append(out.right)
        if out.left:
            stack.append(out.left)
    return path

진행은 다음과 같이 진행된다.

|  | |  | |  | |  | |  |
|  | |  | |  | | 2| | 1|
|  | |  | | 3| | 5| | 5|
|  | | 6| | 9| | 9| | 9|
|11| |16| |16| |16| |16|

언제 사용할 수 있을가

만약 만약 b가 브랜칭 팩터이고, d가 해의 깊이라면, h는 나무의 높이 (d<h)이면 DFS는 O(b^h)시간과 O(h)공간을 사용한다. BFS는 O(b^d)시간과 O(b^d)공간을 사용한다.
일반적인 사용은 다음과 같다.
Find Shortest path — BFS
Test graph bipartiteness — BFS
Find all Connected components — BFS
Find articulation point — DFS
Decision-making tree — DFS
search space whole graph — DFS
Finite children and infinite depth — BFS
The finite depth and infinite children — DFS
Dense graphs — DFS
Sparse graphs — BFS

참고 : https://medium.com/nerd-for-tech/dfs-bfs-introduction-26a65fca2344