사전 曰
- 명사 : 아무렇게나 쌓은 더미
- 동사 : 쌓다.
위키 曰
이진힙은 바이너리 트리의형태를 가진 힙 데이터 구조로 우선순위 queue를 구현하는데 주로 사용된다.
힙이란?
완전한 이진 트리에 기반한 데이터 구조다. 힙은 특정한 순서 속성을 가질 수 있는데. 순서는 두가지가 될 수 있다.
1. max-heap : 각노드의 값은 그들의 부모 노드의 값보다 같거나 작다. 최대값은 root(첫 시작 노드)가 된다. 이와 같은 속성은 모든 노드에 적용된다.
2. min-heap : 각 노드의 값은 그들의 부모 노드의 값보다 같거나 크다.
최소값은 root가 된다. 이와 같은 속성은 모든 노드에 적용된다.
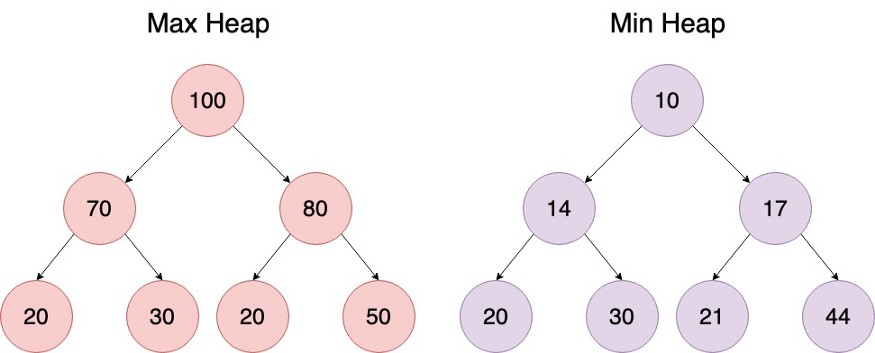
=> 힙은 정렬된 것이 아니다. 각 계층의 노드간의 특정한 관계가 없다. 힙은 완전한 이진 트리기 때문에 N개의 노드를 가진 트리의 높이는 O(log N)을 가진다.
언제 사용할까?
힙은 최대 혹은 최소 값을 삭제할 때 사용한다. 힙은 최대/최소값에 접근하는데 O(1) 시간이 소비된다. 힙은 우선순위 큐를 구현하는데 사용된다.
힙의 단점
최소값과 최대값을 탐색하는데 효과적이지다 하지만 힙은 정렬되지 않았기 때문에 다른 요소를 탐색하기 위해선 O(n)시간이 소비된다.
힙 구현
array를 사용해 최소 힙 구현을 해보겠다.

array의 인덱스는 다음과 같다.
- 부모 노드 의 인덱스 = (i-1)*2
- 왼쪽 자식 노드 인덱스 = 2*i+1
- 오른쪽 자식 노드 인덱스 = 2*i+2
완전한 이진 트리에서 각 레벨은 다른 레벨의 요소가 추가되기 전에 다 채워지며 레벨은 왼쪽에서 오른쪽으로 채워진다.
insertion (삽입)
노드를 삽입하기 위해선
1. 트리의 밑에 노드를 추가한다.
2. 부모노드를 확인한다. 만약 부모 노드가 더 크다면 노드의 값을 교체한다.
3. 비교와 교체를 부모노드가 더 작을 때 까지 반복한다.
비용 강조했듯이 트리의 길이는 log(n)이기 때문에 최악의 시나리오는 새롭게 추가된 노드가 모든 부모노드 보다 작을 때이다. 이때 걸리는 시간적 비용은 O(log (n))이다.
deletion (삭제)
최소 힙에서 root는 이진 힙에서 최소 값이다. 그리고 우리는 그 위치를 정확히 알고 있다. 최소값에 접근 하는 데 드는 비용은 O(1)이다.
만약 노드를 삭제하길 원한다면, 전체 트리를 위로 이동 시킴으로 써 root 노드를 채워 줘야한다.
1. 최하단 오른쪽 노드를 root로 옮기고, 삭제할 노드를 대체한다.
2. 새 노드와 자식노드를 비교하고 자식 노드가 더 크다면 자식 노드중 더 작은 값과 교체한다.
3. 비교와 교체를 반복하고 자식 노드보다 작을 때 까지 반복한다.
비용 삽입과 마찬가지로 최악의 시나리오에서 비용은 O(log(n))이다.
Unodered Arrays에서 heaps으로 전환하기
만약 정렬되지 않은 array를 힙으로 만들고 십다면, 우리는 버블정렬을 사용해서 최대값을 아래로 최소값을 위로 바꾸는 식으로 구현할 수 있다.

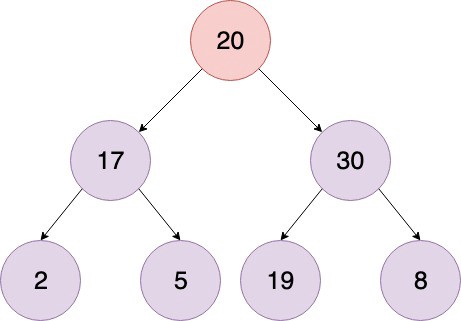
힙으로 바꾸기위해서, 각노드를 자식노드들과 비교해야만한다. 만약 노드가 자식노드 보다 크다면 더 작은 자식노드와 교체해야한다. 즉 최소값이 root가 되도록 버블 정렬을 사용해야한다.
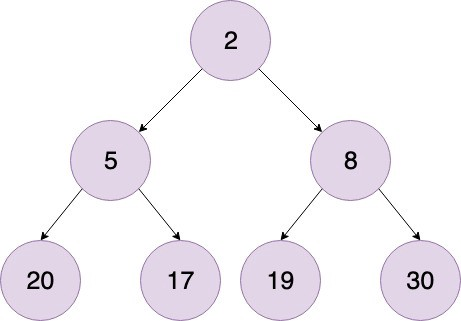
위의 어래이에서 인덱스 0값은 20이고 자식노드는 17과 30이다. 17이 20보다 작기 때문에 둘을 교체한다.

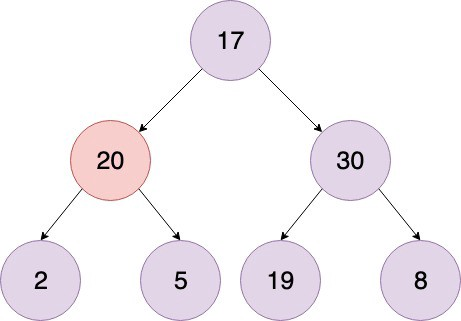
이제 20이 인덱스 1이다. 20의 자식노드는 2와 5입으로 2와 20을 교체한다.

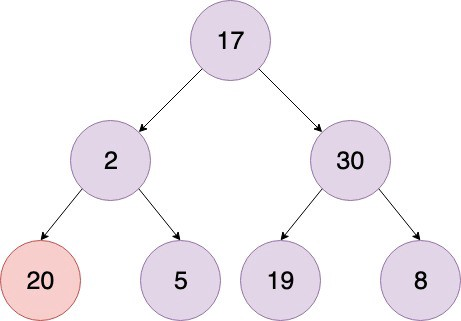
이제 20이 잎사귀 노드가 됐다. 새로운 root 노드는 17이다. 이제 버블정열을 반복한다.

참조 :
https://medium.com/swlh/data-structures-heaps-b039868a521b
https://en.wikipedia.org/wiki/Heap_(data_structure)
