1 단순선형회귀모델을 만들기 위해 전제되어야 하는 조건

1. 변수가 1개일 때 적합하다.

• 독립변수 x만으로 y를 설명할 수 있을 때
• 회귀계수에 대한 검정을 통해 변수 x의 설명력이 존재하는지 확인할 수 있음(p-value 확인)

2. 1차항 이하일 때 적합하다.

• 선형관계

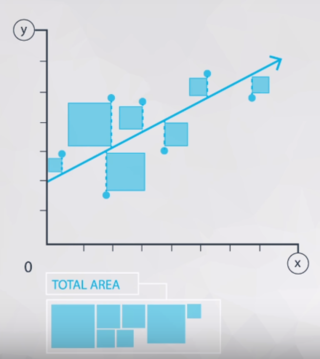
1) 선형성(Linearity) : 독립 변수 X와 종속 변수 Y의 관계는 선형적이어야 한다.
2) 정규성(Normality) : 잔차(예측값과 실제 값의 차이)가 정규 분포여야 한다.
3) 등분산성(Homoscedasticity, Constant Variance) : 독립 변수 X의 모든 값에 대하여 잔차의 분산이 같아야 한다.
4) 독립성(Independence) : 모든 잔차는 독립적이어야 한다.
5) 외생성(Exogeneity, Fixed Features, "Given Constants") : 독립 변수 X는 주어진(고정된) 값이다.
그외 - 다중공선성 부재(Absence of multicollinearity) : 독립 변수들끼리 관련이 없어야 함

2 OLS

잔차란, 실제 값과 추정한 값의 차이를 말한다.

최소자승법(OLS:Ordinary Least Squares)는 잔차제곱합(RSS: Residual Sum of Squares)를 최소화하는 가중치 벡터를 구하는 방법이다.

여기서 RSS는,

위와 같이 표현되며 추정 모델과 데이터 간의 불일치를 측정한 것이다.

따라서 OLS는 이 RSS를 미분하여 그레디언트(gradient) 백터를 구하고, 이 그레디언트 벡터를 0으로 만드는 가중치 벡터를 구하는 것이다.

참고로 잔차 제곱의 합을 구하는 이유는 미분이 가능한 형태로 유일한 해인 최솟값을 구할 수 있기 때문이다.

• scikit-learn 패키지의 LinearRegression 클래스를 통해 나온 coef_가 추정된 가중치 벡터를 의미한다.

참고 : 데이터 사이언스 스쿨 - 선형회귀분석의 기초

3 기준모델 (!= 기본모델)

: 예측 모델을 구체적으로 만들기 전, 가장 간단하면서도 직관적이고 최소한의 성능을 나타내는 기준이 되는 모델.

• 분류문제: 타겟의 최빈 클래스
• 회귀문제: 타겟의 평균값
• 시계열회귀문제: 이전 타임스탬프의 값

그 외 헷갈리던 부분

• 범주형 데이터도 선형관계에 있을 수 있다.

• SSE를 정규화(자유도 n-2로 나눔)한 것이 MSE이다.

• MSE는 actual data와의 차이, R^2는 mean과의 차이이다.

• '선형성'은 독립변수(x)의 차수가 아닌 파라미터가 선형식인지 유무로 결정
  참고 : 선형 회귀 모델에서 '선형'이 의미하는 것은 무엇인가?