자료구조 & 알고리즘 공부 기록(7) - 2024.2.19

동준·2024년 2월 19일

DFS 반복문 백엔드 알고리즘 이중 리스트 이중 반복문 인덱스 자료구조 재귀 재귀함수 트리 파이썬

개인공부(자료구조 & 알고리즘)

목록 보기

7/12

6. 알고리즘 풀이 유형 정리

DFS를 적용하면서 구현할 수 있는 방법에는 반복문과 재귀가 있다. 개인적으로는 재귀를 선호하지 않는다. 반복문과 달리 재귀의 경우에는 종료 조건(정확히는 탈출 조건)을 명시하는 것이 어려우며, 스택 메모리에 지속적으로 쌓이기 때문에 성능이 상대적으로 좋지 않다. 그런 이유로 주로 반복문을 활용해서 문제를 풀었는데...

얼마 전에 푼 DFS 관련 문제에서 등장한 풀이 방식이 재귀로만 구현이 가능한 것 같아서 나름 정리의 필요성을 느낀 김에 유형으로 같이 포함해서 정리하려고 한다. 이거 외에도 n-Queen 문제에서 이중 리스트가 아닌, 단일 리스트의 인덱스를 바탕으로 추적하는 풀이 유형이 트리 부모 관련 문제에서 동일한 방식으로 활용된 김에 얘도 정리해야겠다.

앞으로 문제 풀이가 틀이 갖춰지는 유형들은 이런 식으로 중간에 뜬금없이 목차 중간에서 튀어나와 정리할 예정.

1) 재귀 & 반복문

(1) 왜 고민하는가?

앞서 풀었던 DFS 관련 문제 중에서, 그래프에서 사이클 여부를 판별하는 문제가 있었다. 사이클은 단방향 그래프에서 정점들을 잇는 간선이 기산 정점으로 돌아오는 상황이라고 할 수 있는데. 여기에 만약 DFS로 탐색을 시도하면 아마 완전 탐색을 기반으로 사이클 가능성을 고려하게 된다. 즉, 특정 정점을 기산점으로 삼아 경로들을 전부 탐색하는데, 물론 이것을 아무 조건 설정 없이 수행하면 시간과 메모리 측면에서 낭비가 심할 것이다.

늘 풀던 방식처럼 나는 재귀가 아닌 반복문을 선택해서 DFS를 구현하며 백트랙킹 조건을 설정하려고 했는데, 문제가 생겼다. 이번 탐색은, 특정 정점이 아닌 특정 경로를 대상으로 이뤄지기 때문에 겹치는 탐색 수행이 꽤 많다는 점.

즉, 반복 분기에서의 탐색 경로 기억만으로는 분기가 종료되는 시점에서 다음 분기를 위해서 탐색 경로 기억을 비워줘야 하므로, 경로 기억을 유지할 수 없기 때문에 결국 같은 곳을 다시 방문하는 케이스가 생길 수 밖에 없는 것이다.

(2) DFS에서의 사이클 탐색

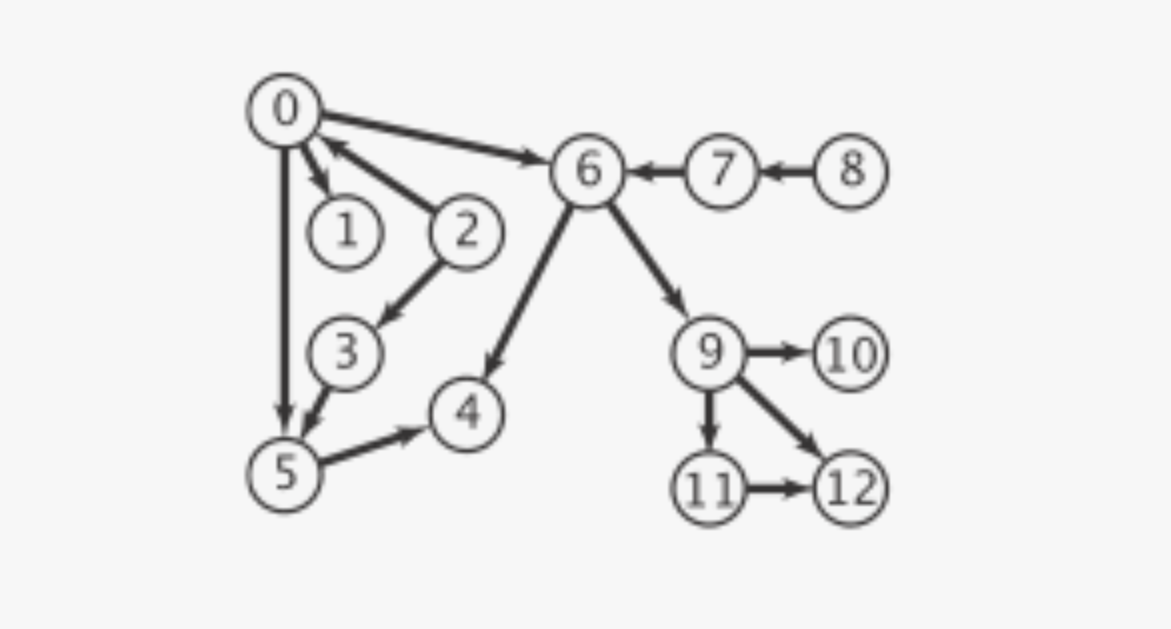
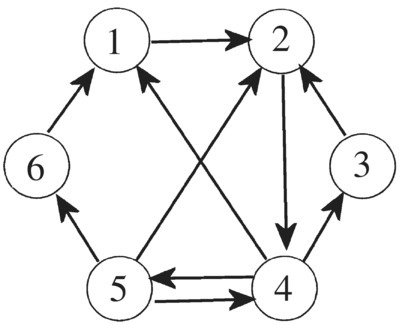
위의 그래프를 예시로 들어서 만약 DFS를 반복문으로 구현해서 사이클 여부를 판별한다고 생각하자. 현재 분기에서의 기산점은 정점 0이고, 현재 분기에서 탐색 방향은 정점 6을 통해 우하귀 쪽으로 진입한다.

해당 분기에서 6번 정점으로 향하는 모든 길목을 보다시피 사이클을 이루지 않는 것을 확인할 수 있지만, 이것에 대한 기억 또한 별도로 처리해야 한다. 왜냐하면 현재 분기에서의 경로 기억은 다음 분기에서 리셋되기 때문이다.

문제는, 파이썬이나 자바는 포인터를 다루지 않기 때문에 그래프에서의 간선 정보를 직접 제어할 수 없다. 즉, 우리가 간선이라 인지하고 있는 것은 실제 상술한 언어 상에서는 정점(노드)의 참조 객체를 통해 방향만을 짐작할 뿐이지 간선의 방향에 대해서는 직접적으로 제어할 수 없다.

결국 경로에 대한 기억은 방문했던 정점에 대한 기억이 되는데, 이 정점의 추가 시점이 중요하다. 아직 탐색이 종료되지 않은 시점에서 정점 6에 대해서 사이클 가능성이 없다고 판별하면 안되기 때문에, 탐색이 전부 종료된 후에야 사이클 가능성이 없다는 별도의 기억 처리를 수행해야 하기 때문이다.

(3) 경로에 대한 기억 처리

더 이상 해당 정점이 사이클을 그리지 않는다고 판별하는 시점은, 해당 분기에서의 탐색이 종료되는 시점이어야 한다. 이것을 반복문에서 처리하려고 시도했을 때는 반복 분기에서 그 시점에서의 탐색에 대한 기억 처리는 쉽게 이뤄졌지만 탐색 종료 시점에서의 해당 정점에 대한 사이클 가능성 판단을 수행하는 것이 (재귀로 표현한 이상 아마 가능하겠지만 내 수준에서는) 불가능했다.

왜냐하면 반복문의 단위 분기가 종료되면, 해당 코드에서는 그 분기를 기억하지 않고 단위 처리가 종료됐다고 판단하기 때문에 해당 탐색에서 밟았던 경로에 대한 사이클 불가능 처리를 동시에 수행할 수 없었다.

하지만 재귀는 가능했다. 정확히는 재귀의 문법에 대한 숙지가 필요했다.

def recusive(n):
	# exit
    if exit:
    	return 0
    
    # recursion
    # ...
    recursive(n+1)

기본적인 재귀 함수는 탈출 조건과 재귀 조건으로 구성된다. 재귀 함수의 기본적인 동작은 재귀적인 호출을 통한 쌓아올림이 된다. recursive() 함수가 지속적으로 호출되면서 쌓이다가 exit 조건에 다다르면 탈출 조건이 발동되면서 맨 위에 쌓였던 재귀함수가 리턴되면서 종료되고, 이전에 호출됐던 함수들 역시 순차적으로 종료된다.

여기에 코드를 하나 추가하게 되면...

def recusive(n):
	# exit
    if exit:
    	return 0
    
    # recursion
    # ...
    recursive(n+1)
    
    # additional
    another_condition

탈출 조건이 호출되는 재귀 함수는 가장 마지막에 호출된(가장 상단에 쌓인) 함수다. 그리고 순차적으로 쌓였던 재귀 함수들은 탈출 조건이 아닌 재귀 호출 아래에 적혀진 실행 블록의 맨 마지막까지 실행된 다음에 종료된다.

즉, 위의 코드에서 말단의 재귀 함수가 리턴되면서 종료되고 이전 순차의 재귀함수는 재귀 호출의 하부에 작성된 추가 코드, another_condition이 실행되면서 종료되는 것이다. 이것을 사이클 기억에서 적용할 수 있다.

현재 분기에서의 탐색 기억 : 재귀 호출 직전에 추가한다.

전체 반복에서의 사이클 가능성 판별 기억 : 재귀 호출 종료 후에 추가한다.

즉, 탐색 이후의 종료 역시 순차적으로 이뤄진다는 점을 재귀에 접목시킬 수 있는 것이다.

2) 리스트의 인덱스

(1) 이중 리스트의 비효율성

리스트의 요소로 리스트를 두면 그건 이중 리스트가 된다. 이중 리스트의 장점은 특정 요소가 지니는 정보를 대량으로 기억시킬 수 있다는 점이며, 나 역시 알고리즘 풀이에서 자주 애용했었다. 하지만, 알고리즘 공부를 본격적으로 시작한 이후로는 이중과 관련된 키워드를 최대한 멀리하려고 하고 있다.

외부 인덱스가 n-1까지 있고, 내부 요소의 인덱스도 n-1까지 있으면, 시간복잡도는 O(n^2)이 계산된다. 보통 시간복잡도가 저렇게 계산된다면 웬만한 알고리즘 풀이는 불통과라고 봐도 무방하다. 가장 확실하지만 가장 최악의 탐색 방법이기 때문.

시간복잡도가 O(n^2)이 나오는 경우는 이중 반복문이 있다. 이중 리스트에서의 특정 요소 검색 역시 이중 반복문의 매커니즘과 똑같이 이뤄지기 때문에 똑같은 시간복잡도가 계산되기 때문에 최대한 지양하는 것이 옳다.

(2) n-Queen 문제

[
 [0, 0, 0, 0, 1],
 [0, 1, 0, 0, 0],
 [0, 0, 1, 0, 0],
 [0, 0, 0, 0, 1],
 [1, 0, 0, 0, 0]
]

위와 같은 이중 리스트가 있다. n-Queen 문제에서는 위를 체스보드처럼 생각해서 문제를 풀이하려고 했다. 요소들 중에서 1, 즉 통행 가능한 경로를 행 단위에서 순차적으로 탐색해야 한다.

하지만 저렇게 되면 우선 외부 리스트를 먼저 검색해서 행에 대한 정보를 파악하고, 또 그 행 내부에 들어가서 몇 번째가 통행 가능한 경로인지에 대해 파악하는 이중 작업이 수행된다. 가독성은 좋지만 그만큼 고려할 점이 많아져서 문제풀이에서 실수가 많이 나왔다.

다음은 이를 단일 리스트로 수행한 똑같은 표현이다.

[4, 1, 2, 4, 0]

이는 인덱스를 행의 순서, 요소의 값을 내부 리스트에서의 통로 인덱스로 표현한 것이다. 물론 이런 식으로 표현하는 것은 경로 탐색의 대상이 되는 그래프가 n*n 형태의 정사각형일 때만 가능하지만 적어도 이중 리스트를 지양한다는 소기의 목적은 달성할 수 있다.

(3) 트리 구조에서의 부모 추적

트리 문제를 풀 때 자주 나왔던 유형이 정점에 대한 정보들만 제시하고 부모, 자식 관계를 판별하는 문제가 나왔다. 어차피 정점에 대해서는 부모 혹은 자식이라는 이지선다밖에 없기 때문에 한 정점(보통은 루트 노드가 될 것이다)의 부모, 자식 관계를 판명하면 줄줄이 소세지처럼 다른 정점들의 부모, 자식 여부를 결정하게 된다.

(내가 문제를 풀 때) 저런 문제에서 핵심적으로 필요한 것은 부모 추적 리스트인데, 생각했던 풀이 방식은 다음과 같았다.

어차피 노드는 부모, 자식 둘 중 하나다.

그렇기에 초기에는 무방향 그래프로 간선 정보를 파악해야 한다.

루트 노드를 판별하고, 루트 노드에 연결된 다른 노드들은 전부 자식 노드(Level 1)가 된다.

루트 노드를 판별하는 것은 쉬웠고, 그를 통해 깊이 1에 해당하는 노드들 역시 판별할 수 있었다. 그 이후는 어떻게 할 것인가? 여기에서 부모 추적 리스트를 도입해야 하는 것이다.

예를 들어서 노드가 7개 주어졌고, 0번 노드가 루트 노드라고 가정했을 때, 아래와 같은 부모 추적 리스트를 선언한다.

# 부모 추적 리스트
# 리스트의 '인덱스'는 '자식 노드'
# 리스트의 '요소'는 '자식 노드(인덱스)의 부모 노드'
parent_list = [-1, None, None, None, 0, None, 0]

루트 노드는 부모가 없기 때문에 임의로 -1을 부여하고, 0을 부모로 가지는 자식 노드는 위의 리스트에 따르면 4와 6이 된다. 이것을 이렇게 표현할 수 있다.

parent_list[child] = parent

즉 자식 노드를 인덱스로 삼아서 부모 노드를 추적할 수 있게 하는 것이다. 여기서 조금 더 이어보자면, 부모 추적은 결국 BFS로 이뤄져야 할 것이다. 왜냐하면 루트 노드로부터 이뤄지는 탐색이 너비를 기반으로 이뤄져야 레벨 단위로 부모, 자식 관계를 명확화시킴으로써 다음 탐색 노드의 종류를 제어해야 하기 때문이다.

앞전에 만들어둔 양방향 그래프를 통한 간선 정보를 바탕으로 자식으로 확인된 노드를 다시 큐에서 팝해서 부모로 삼은 후, 해당 노드의 간선으로 이어진 노드들을 순회 후, 자식으로 삼는다. 이때, 부모 추적 리스트[간선으로 이어진 노드] = 해당 노드가 되면서 부모 추적 리스트를 채워서 추적되지 않은 노드들을 분별할 수 있게 해준다.