문제 링크: https://www.acmicpc.net/problem/1389

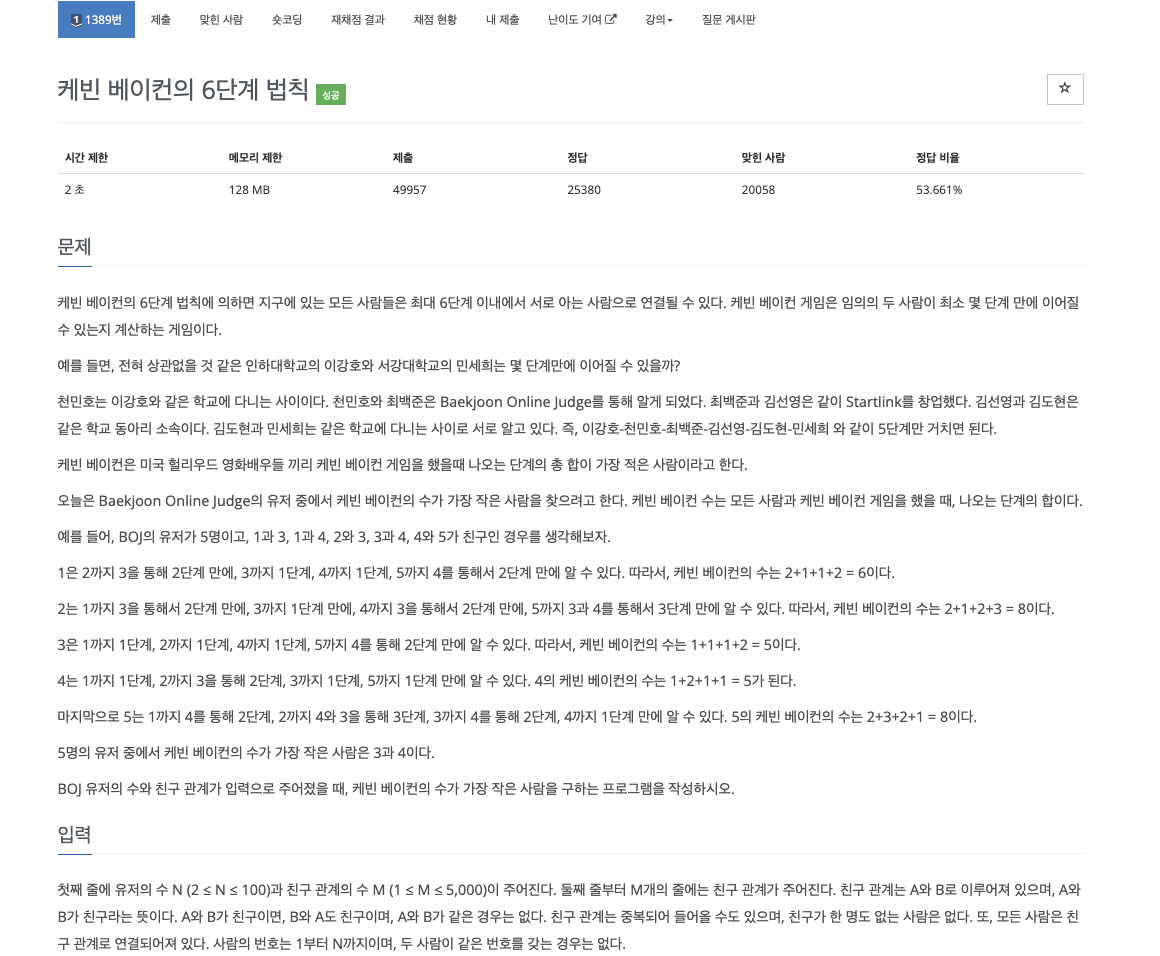
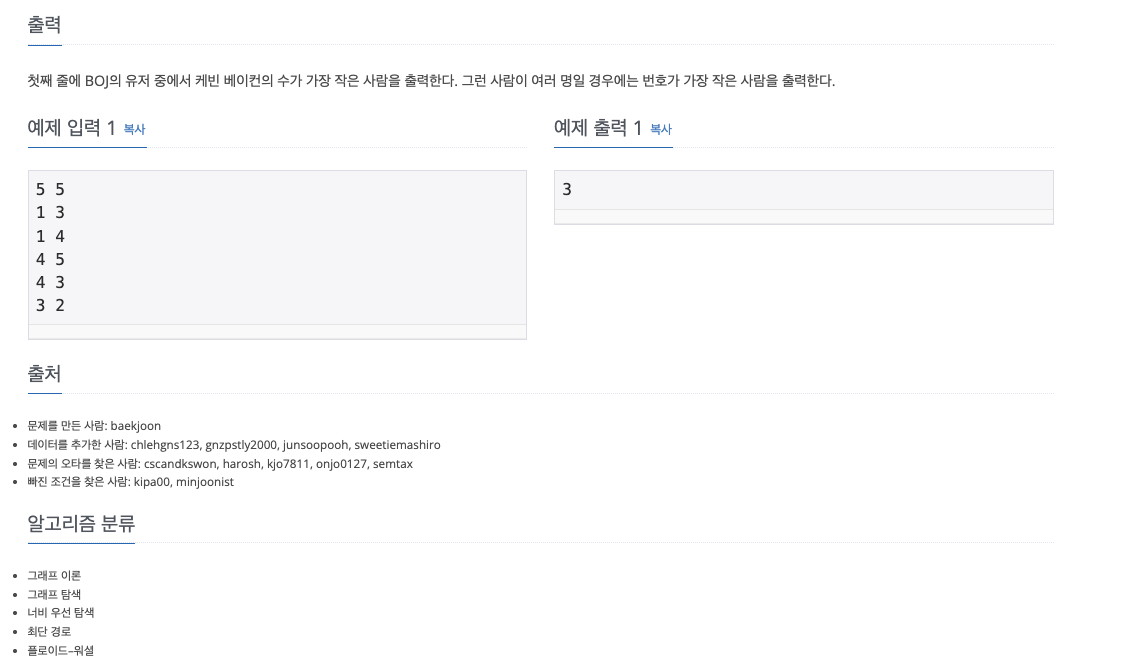
문제

해설

시작점이 존재하지 않고, 모든 노드에서 다른 노드까지의 최단 거리를 구해야 하기 때문에 전형적인 플로이드-워셜 알고리즘이다. 또한 문제 특성상 시작 노드에서 현재 노드까지의 깊이(거리)를 기록 및 갱신하면서 그래프를 전체 탐색하여도 문제가 풀리기 때문에 BFS를 사용하여 문제를 풀어도 무방하다.

BFS, 플로이드-워셜 두 가지 방법으로 문제를 풀어보겠다.

BFS 풀이

Java

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;

public class Main {
    static int N, M;
    static List<Integer>[] graph;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringBuilder sb = new StringBuilder();
        StringTokenizer st = new StringTokenizer(br.readLine(), " ");

        N = Integer.parseInt(st.nextToken()); // 유저(노드)의 수
        M = Integer.parseInt(st.nextToken()); // 인맥(간선)의 수

        graph = new ArrayList[N + 1]; // 유저(노드)간의 관계가 저장된 인맥(그래프) - 인접 배열
        for (int i = 1; i <= N; i++) {
            graph[i] = new ArrayList<>();
        }

        while (M-- > 0) {
            st = new StringTokenizer(br.readLine());
            int a = Integer.parseInt(st.nextToken());
            int b = Integer.parseInt(st.nextToken());
            /*무방향 그래프이기 때문에 양쪽에 모두 저장*/
            graph[a].add(b);
            graph[b].add(a);
        }

        int minCount = Integer.MAX_VALUE; // 현재까지의 최소 케빈 베이컨의 수
        int minIdx = 0; // 현재까지의 최소 케빈 베이컨의 수를 가진 사람

        for (int i = 1; i <= N; i++) {
            // bfs: 해당 유저(노드) i의 케빈 베이컨의 수를 구하기 위한 bfs
            int count = bfs(i);
            if (minCount > count) { // 현재 유저 i의 케빈 베이컨이 현재의 최소 케빈 베이컨보다 더 작다면
                minCount = count; // 유저 i의 케빈 베이컨 수로 최소 베이컨 갱신
                minIdx = i; // 최소 유저를 i로 갱신
            }
        }
        sb.append(minIdx);
        System.out.println(sb);

    }

    private static int bfs(int user) {
        int count = 0; // 해당 유저(노드)의 현재까지의 케빈 베이컨 수 카운트
        int[] dist = new int[N + 1]; // 해당 유저에서 각 다른 유저들과의 단계(거리) 수를 저장하는 배열
        Arrays.fill(dist, -1); // 다른 모든 유저들간의 거리 -1로 초기화(-1이면 해당 유저과의 거리는 아직 계산하지 않은 거고 0이면 유저 본인)
        Queue<Integer> queue = new ArrayDeque<>(); // bfs 수행을 위한 큐

        queue.offer(user);
        dist[user] = 0; // 유저 자기 자신(현재 시작 노드)과의 거리는 0

        while (!queue.isEmpty()) {
            int cur = queue.poll();
            for (int next : graph[cur]) {
                if (dist[next] == -1) { // 아직 거리를 계산하지 않은(거리가 -1인) 인접 유저라면
                    dist[next] = dist[cur] + 1; // cur의 인접 노드인 next 노드는 cur 노드보다 시작 노드에서 +1 더 떨어져 있다 
                    count += dist[cur]; // 케빈 베이컨 수: 구하고자 하는 기준 노드에서 다른 모든 노드와의 거리의 총합이기 때문에 현재 살펴보는 노드와의 거리 누적합하기
                    queue.offer(next);
                }
            }
        }

        return count; // 파라미터 user 노드의 케빈 베이컨 수 최종 반환
    }


}

Python

import sys
from collections import deque

input = sys.stdin.readline

N, M = map(int, input().split())  # N: 유저(노드)의 수, M : 인맥(엣지)의 수

graph = [[] for _ in range(N + 1)]  # 노드간의 관계를 나타내는 인접 리스트
for _ in range(M):
    a, b = map(int, input().split())
    graph[a].append(b)
    graph[b].append(a)


def bfs(x):
    dist = [-1] * (N + 1)  # 현재 노드 x와 다른 노드들간의 거리를 나타내는 리스트(-1은 거리 미갱신, 0은 자기 자신)
    count = 0 # 현재 노드 x의 케빈 베이컨의 수
    queue = deque([x])
    dist[x] = 0  # 시작 노드 x의 거리 0으로 갱신
    while queue:
        cur = queue.popleft()  # x와의 거리를 구할 현재 노드
        for next in graph[cur]:  # cur 노드와의 인접 노드들
            if dist[next] == -1:  # 아직 해당 인접 노드와 거리 갱신이 되지 않았다면
                dist[next] = dist[cur] + 1  # 인접 노드는 cur 노드보다 시작 노드와 +1 더 멀다
                count += dist[cur]  # 케빈 베이컨 수를 구하기 위해 시작 노드와 cur 노드와의 거리 누적합
                queue.append(next)

    return count


min_count = sys.maxsize  # 현재의 최소 케빈 베이컨 수
min_idx = 0  # 현재의 최소 케빈 베이컨 수를 가진 유저

for i in range(1, N + 1):
    count = bfs(i)  # i 노드의 케빈 베이컨 수(다른 노드들과의 거리의 총합)을 구하기 위해 bfs 수행
    if min_count > count:  # 만약 최소 케빈 베이컨 수가 나온다면 최소 케빈 베이컨 수, 최소 유저 갱신
        min_count = count
        min_idx = i

print(min_idx)

플로이드-와샬

플로이드-워셜 알고리즘은 그래프에서 모든 정점 간의 최단 경로를 구하는 알고리즘으로 다익스트라 알고리즘처럼 단일 출발점에서 다른 정점들까지의 최단 경로를 구하는 것이 아니라, 모든 쌍의 정점 간 최단 경로를 한 번의 실행으로 계산한다.

플로이드-워셜은 동적 프로그래밍을 기반으로 동작한다.

정 두 정점 u,v 사이의 최단 경로는, 다른 정점 k를 거쳐가는 경우와 거치지 않는 경우 중 더 짧은 경로로 갱신되는데 이를 수식으로 나타내면 다음과 같다:

d[i][j]=min(d[i][j], d[i][k]+d[k][j])

Java

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;

public class Main {
    static int N, M;
    static long[][] graph;
    static final int INF = Integer.MAX_VALUE; // 무한대(아직 최단거리 갱신하지 않은 노드들간의 초기값)

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringBuilder sb = new StringBuilder();
        StringTokenizer st = new StringTokenizer(br.readLine());

        N = Integer.parseInt(st.nextToken());
        M = Integer.parseInt(st.nextToken());

        graph = new long[N + 1][N + 1]; // 노드 연결 정보를 나타내는 2차원 인접 행렬
        for (int i = 1; i <= N; i++) {
            for (int j = 1; j <= N; j++) {
                if (i == j) graph[i][j] = 0;  // 자기 자신과의 거리는 0
                else graph[i][j] = INF; // 다른 노드과의 거리는 무한대로 초기화
            }
        }

        while (M-- > 0) {
            st = new StringTokenizer(br.readLine());
            int a = Integer.parseInt(st.nextToken());
            int b = Integer.parseInt(st.nextToken());
            graph[a][b] = graph[b][a] = 1; // 연결되어 있는 인접 노드들끼리는 인접 행렬에 0으로 표시(무방향 그래프이기 때문에 양방향 표시)

        }

        long minCount = INF; // 현재의 최소 케빈 베이컨 수
        int minIdx = 0; // 현재의 최소 유저

        floydWarshall(); // 플로이드 워셜 실행해서 인접행렬 그래프 형태로 노드들간의 최단 거리 전부 갱신
        
        for (int i = 1; i <= N; i++) {
            long count = Arrays.stream(graph[i]).sum(); // i 노드와 다른 모든 노드들간의 거리 총합으로 구한 케빈 베이컨 수(i행의 데이터 총합)
            if (minCount > count) { // 현재의 최소 케빈 베이컨 수보다 i 노드의 케빈 베이컨이 더 작다면 갱신
                minCount = count;
                minIdx = i;
            }
        }

        sb.append(minIdx);
        System.out.println(sb);

    }
    
    private static void floydWarshall() {
        for (int k = 1; k <= N; k++) { // k : 출발 지점과 도착 지점 사이의 경유지
            for (int i = 1; i <= N; i++) { // i : 출발 지점
                for (int j = 1; j <= N; j++) { // j : 도착 지점
//                    if (graph[i][j] > graph[i][k] + graph[k][j]) graph[i][j] = graph[i][k] + graph[k][j];
                    graph[i][j] = Math.min(graph[i][j], graph[i][k] + graph[k][j]); // 기존 i와 j간의 최단 경로와 새로운 경유지인 k를 거친 i와 j간의 거리를 비교하여 최단 거리 갱신
                }
            }
        }

    }
}

Python

import sys
input = sys.stdin.readline
inf = float('inf')

N, M = map(int, input().split())
graph = [[0 for _ in range(N + 1)] for _ in range(N + 1)]

for i in range(1, N + 1):
    for j in range(1, N + 1):
        if (i != j): graph[i][j] = inf

for _ in range(M):
    a, b = map(int, input().split())
    graph[a][b] = graph[b][a] = 1


def floyd_warshall():
    for k in range(1, N + 1):
        for i in range(1, N + 1):
            for j in range(1, N + 1):
                graph[i][j] = min(graph[i][j], graph[i][k] + graph[k][j])


floyd_warshall()

min_count = inf
min_idx = 0

for i in range(1, N + 1):
    count = sum(graph[i])
    if min_count > count:
        min_count = count
        min_idx = i

print(min_idx)