문제 설명

메리는 여름을 맞아 무인도로 여행을 가기 위해 지도를 보고 있습니다. 지도에는 바다와 무인도들에 대한 정보가 표시돼 있습니다. 지도는 1 x 1크기의 사각형들로 이루어진 직사각형 격자 형태이며, 격자의 각 칸에는 'X' 또는 1에서 9 사이의 자연수가 적혀있습니다. 지도의 'X'는 바다를 나타내며, 숫자는 무인도를 나타냅니다. 이때, 상, 하, 좌, 우로 연결되는 땅들은 하나의 무인도를 이룹니다. 지도의 각 칸에 적힌 숫자는 식량을 나타내는데, 상, 하, 좌, 우로 연결되는 칸에 적힌 숫자를 모두 합한 값은 해당 무인도에서 최대 며칠동안 머물 수 있는지를 나타냅니다. 어떤 섬으로 놀러 갈지 못 정한 메리는 우선 각 섬에서 최대 며칠씩 머물 수 있는지 알아본 후 놀러갈 섬을 결정하려 합니다.

지도를 나타내는 문자열 배열 maps가 매개변수로 주어질 때, 각 섬에서 최대 며칠씩 머무를 수 있는지 배열에 오름차순으로 담아 return 하는 solution 함수를 완성해주세요. 만약 지낼 수 있는 무인도가 없다면 -1을 배열에 담아 return 해주세요.

제한 사항

• 3 ≤ maps의 길이 ≤ 100
• • 3 ≤ maps[i]의 길이 ≤ 100
• • maps[i]는 'X' 또는 1 과 9 사이의 자연수로 이루어진 문자열입니다.
• • 지도는 직사각형 형태입니다.

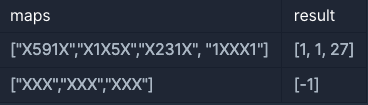
입출력 예

정답 코드

import java.awt.*;
import java.util.List;
import java.util.Queue;
import java.util.*;

public class Solution {

    static int n;
    static int m;
    static boolean[][] visited;
    static char[][] graph;
    static int sum;
    static List<Integer> result;

    public int[] solution(String[] maps) {

        n = maps.length; // 세로
        m = maps[0].length(); // 가로
        visited = new boolean[n][m];
        graph = new char[n][m];
        result = new ArrayList<>();  // 리스트 초기화

        // 그래프 초기화
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                graph[i][j] = maps[i].charAt(j);
            }
        }

        // 각 좌표에서 BFS 수행
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (Character.isDigit(graph[i][j]) && !visited[i][j]) { // 숫자이고 방문하지 않은 경우에만 BFS 수행
                    sum = 0;
                    bfs(i, j);
                    result.add(sum); // BFS 끝난 후 합계를 result에 추가
                }
            }
        }

        // 결과를 정렬
        Collections.sort(result);

        // result 리스트가 비어 있으면 [-1] 반환
        if (result.isEmpty()) {
            return new int[]{-1};
        }

        // 리스트를 배열로 변환하여 반환
        return result.stream().mapToInt(i -> i).toArray();
    }

    private void bfs(int x, int y) {

        Queue<Point> queue = new LinkedList<>();
        queue.add(new Point(x, y));
        visited[x][y] = true;
        sum += Character.getNumericValue(graph[x][y]); // 현재 좌표의 숫자를 합산

        int[] dx = {1, -1, 0, 0}; // 상하 이동
        int[] dy = {0, 0, 1, -1}; // 좌우 이동

        while (!queue.isEmpty()) {
            Point curPoint = queue.poll();

            for (int i = 0; i < 4; i++) {
                int nx = curPoint.x + dx[i];
                int ny = curPoint.y + dy[i];

                if (nx < 0 || nx >= n || ny < 0 || ny >= m || visited[nx][ny] || !Character.isDigit(graph[nx][ny])) {
                    continue;
                }

                queue.add(new Point(nx, ny));
                visited[nx][ny] = true;
                sum += Character.getNumericValue(graph[nx][ny]); // 숫자값을 sum에 더함
            }
        }
    }


}

매우 전형적인 그래프 완전탐색 문제이다.