import numpy as np
X = np.array([
[0,0,1],
[0,1,1],
[1,0,1],
[1,1,1]
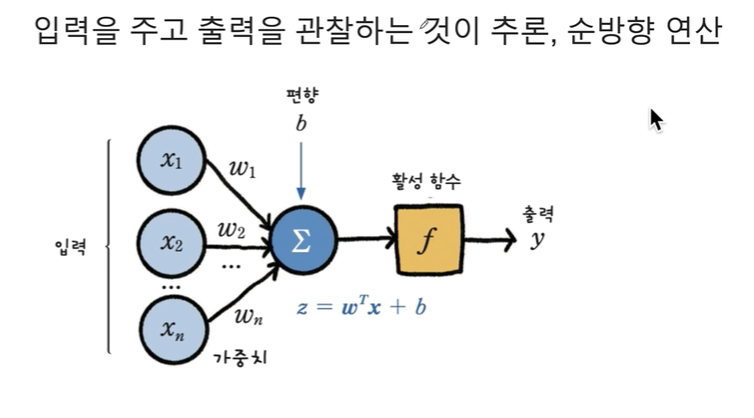
])def sigmoid(x):
return 1.0 / (1.0 + np.exp(-x))W = 2*np.random.random((1,3)) -1
Warray([[-0.35626925, -0.54131108, 0.80274536]])
확인할 수 있다.가중치를 랜덤하게 선택했기에
원래는 학습이 완료된 가중치를 사용해야 한다.
추론 결과
n=4
for k in range(n):
x = X[k, :].T
v = np.matmul(w,x)
y = sigmoid(v)
print(v)값을 확인할 수 있었다.
하지만 문제!!
랜덤하게 잡았기 때문에 추론 결과는 아무런 의미가 없거나 틀렸다
이제 가중치가 정답을 맞추도록 학습을 시켜야 한다.
D = np.array([
[0],[0],[1],[1]
])그래서 우선 정답을 먼저 입력해주자
def calc_output(W,x):
v = np.matmul(w,x)
y = sigmoid(v)
return y오차율 계산
def calc_error(d,y):
e = d-y
delta = y*(1-y) * e
return deltadef delta_GD(W,X,D,alpha):
for k in range(4):
x = X[k,:].T
d=D[k]
y = calc_output(W,x)
delta = calc_error(d,y)
dW = alpha*delta*x
W = W+dW
return W
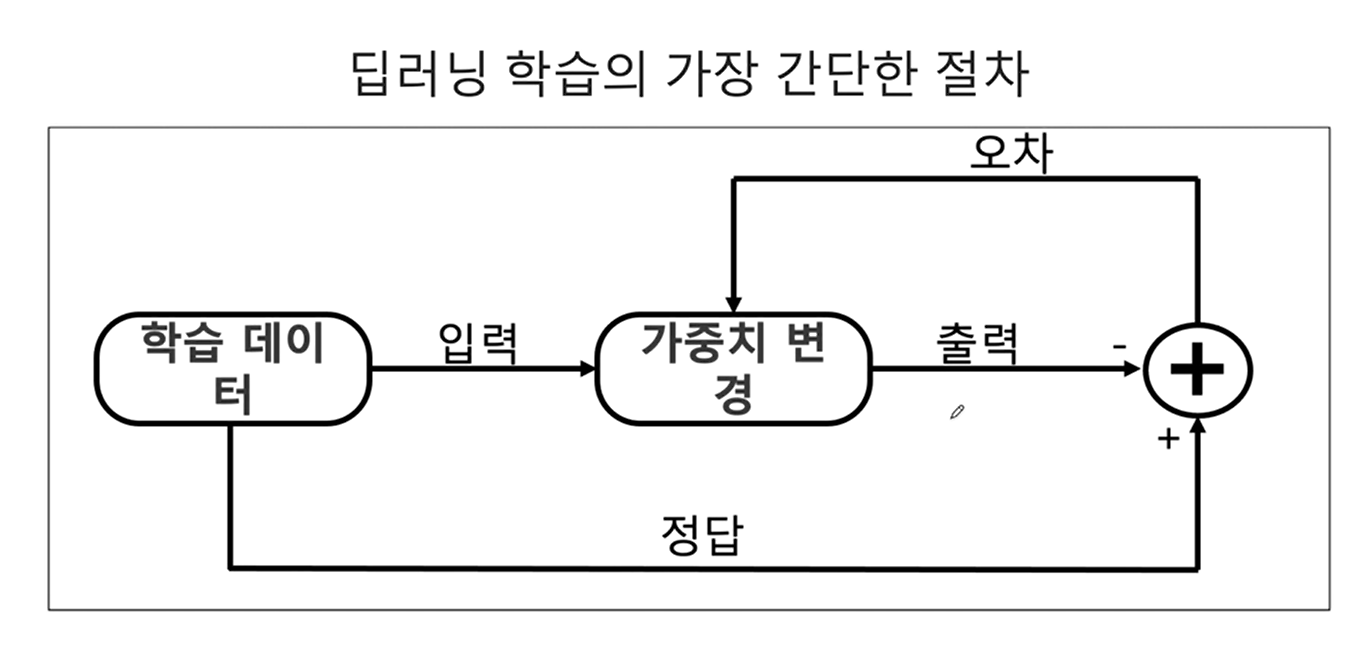
그림과 같이 학습을 시키도록 할 것이다.
W =2*np.random.random((1,3))-1
alpha = 0.9
for epoch in range(10000):
W = delta_GD(W,X,D,alpha)
print(W)이렇게 하면 결과가 너무 많이 나와서,,몇개만 적어보자면
[[ 21.87266777 -26.76735849 -60.37668481]]
[[ 21.94403079 -26.85096037 -60.56602104]]
[[ 22.01539381 -26.93456225 -60.75535728]]
[[ 22.08675684 -27.01816413 -60.94469351]]
[[ 22.15811986 -27.10176601 -61.13402975]]
[[ 22.22948288 -27.18536789 -61.32336599]]
[[ 22.3008459 -27.26896977 -61.51270222]]
[[ 22.37220893 -27.35257165 -61.70203846]]
[[ 22.44357195 -27.43617353 -61.8913747 ]]
[[ 22.51493497 -27.51977541 -62.08071093]]
등의 결과가 만개 나온다.
N=4
for k in range(N):
x = X[k, :].T
v = np.matmul(W,x)
y = sigmoid(v)
print(v)
w결과 확인 [0.01020176][0.00829464] [0.99324188][0.99168508]
XOR을 활용해서 더 알아보기
X = np.array([
[0,0,1],
[0,1,1],
[1,0,1],
[1,1,1]
])
D= np.array([
[0],[1],[1],[0]
])
W = 2*np.random.random((1,3)) -1alpha = 0.9
for epoch in range(1000):
W = delta_GD(W,X,D,alpha)N = 4
for k in range(N):
x = X[k,:].T
v = np.matmul(W,x)
y = sigmoid(v)
print(y)[9.87437471e-68][1.17742856e-88]
[2.1557588e-113][2.57054453e-134]
def calc_output(W1,W2,x):
v1 = np.matmul(W1,x)
y1 = sigmoid(v1)
v = np.matmul(W2,y1)
y = sigmoid(v)
return y,y1출력층의 델타 계산
def calc_delta(d,y):
e = d-y
delta = y*(1 - y) * e
return delta은닉층의 델타 계산
def calc_delta1(W2,delta,y1):
e1 = np.matmul(W2.T, delta)
delta1 = y1 * (1-y1) * e1
return delta1역전파 코드
def backprop_XOR(W1, W2, X, D, alpha):
for k in range(4):
x = X[k, :].T
d = D[k]
y, y1 = calc_output(W1, W2, x)
delta = calc_delta(d,y)
delta1 = calc_delta1(W2,delta, y1)
dW1 = (alpha * delta1).reshape(4, 1) * x.reshape(1, 3)
W1 = W1 +dW1
dW2 = alpha * delta * y1
W2 = W2 +dW2
return W1, W2,X = np.array([
[0,0,1],
[0,1,1],
[1,0,1],
[1,1,1]
])
D= np.array([
[0],[1],[1],[0]
])
W1 = 2 * np.random.random((4,3)) - 1
W2 = 2 * np.random.random((1,4)) - 1
alpha =0.9
for epoch in range(1000):
W1, W2 = backprop_XOR(W1, W2 ,X, D, alpha)이제 결과를 다시 확인해보자
N = 4
for k in range(N):
x = X[k,:].T
v1 = np.matmul(W1,x)
y1 = sigmoid(v1)
v = np.matmul(W2,y1)
y = sigmoid(v)
print(y)이렇게 하면 결과가 0, 1, 1, 0 이 나오는 것을 확일할 수 있다.