1. 문제
-
지역의 높이 정보에 따라 비가 왔을 때 물에 잠기지 않는 “안전영역”의 최대 개수는?
-
잠기지 않은 부분들의 최대 영역이 안전지대
- 높이가 4이하가 모두 물에 잠겼을 경우 ⇒ 5개
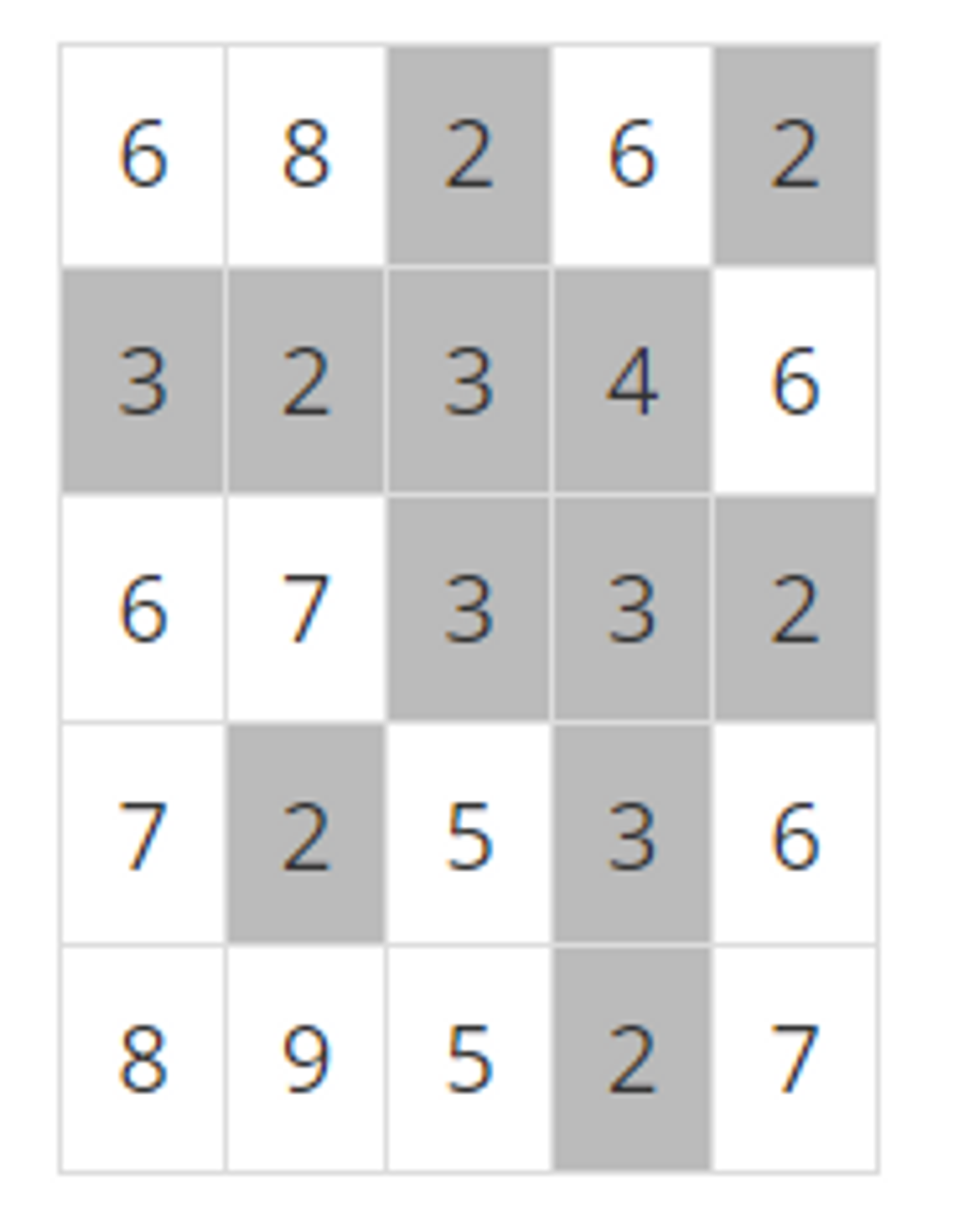
- 높이가 6이하인 지점이 모두 잠겼을 경우 ⇒ 4개
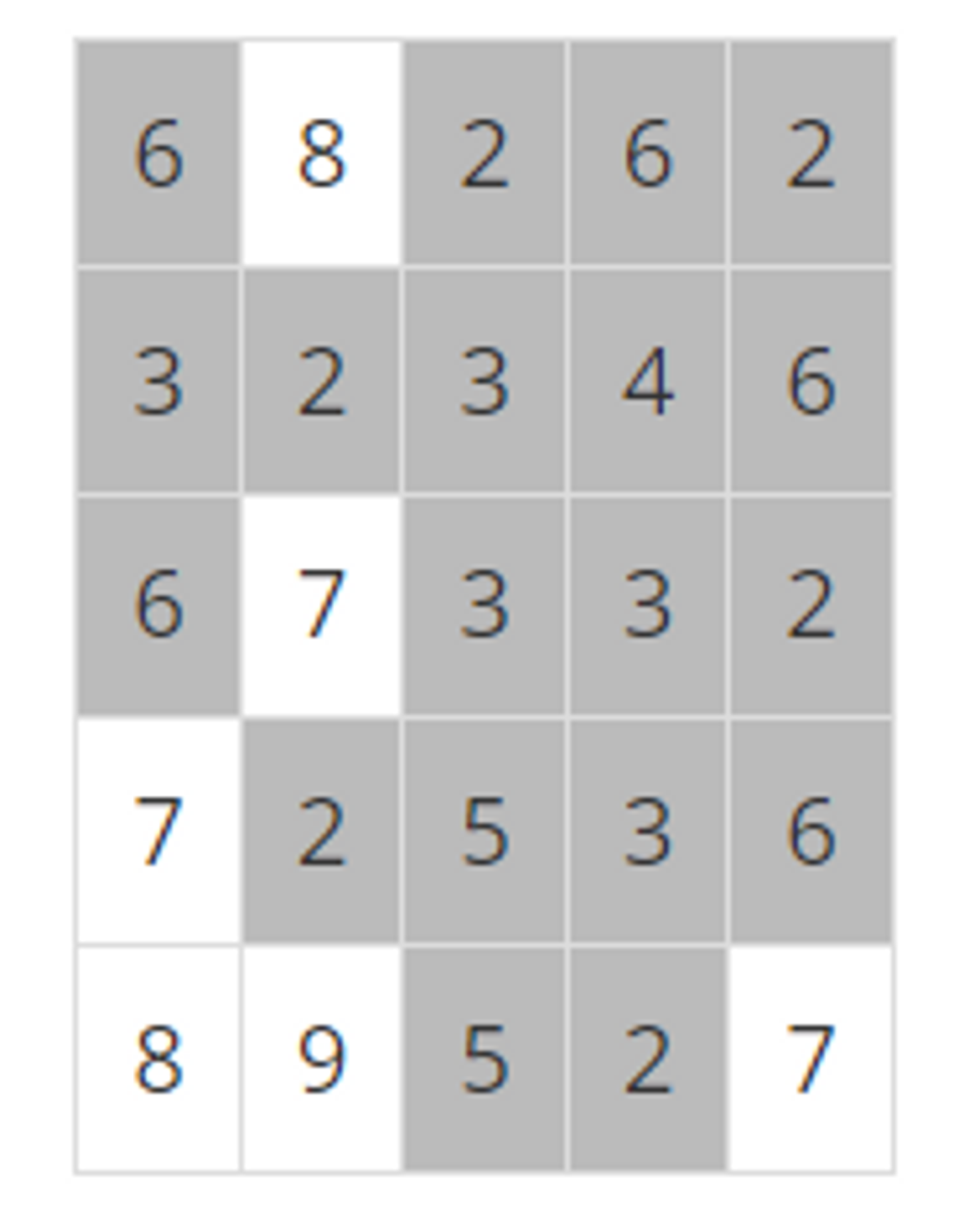
- 높이가 4이하가 모두 물에 잠겼을 경우 ⇒ 5개
-
-
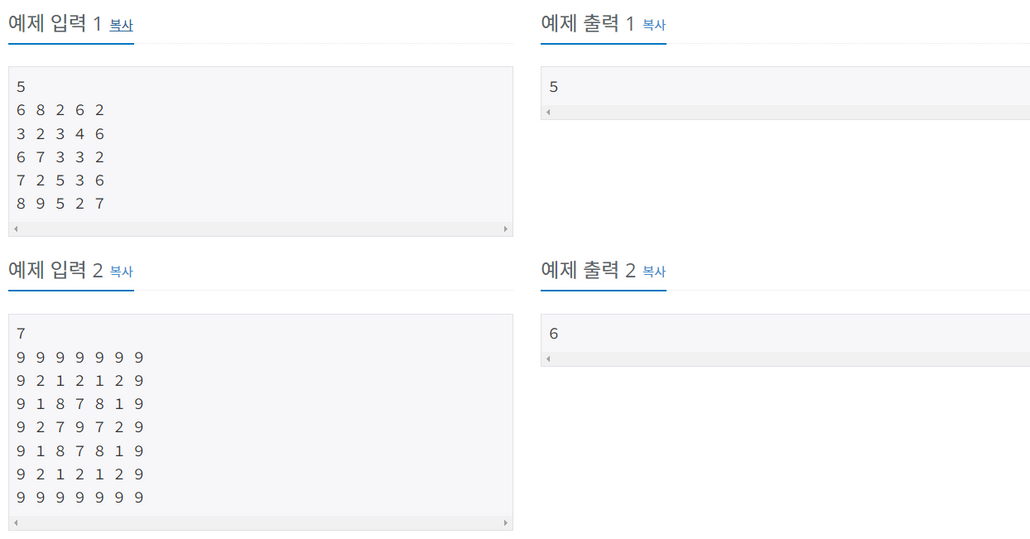
입력
1| 행/열의개수
이후 | 높이 정보- 출력
안전한 영역의 최대 개수
2. 풀이
- BFS! - queue를 활용해서 안전지대의 개수를 구한다
- 최대 개수를 구해야하므로, 주어진 높이들 중 최대 높이를 구한 뒤
0부터 최대높이-1까지 강수량을 설정하여 각 강수량에 따른 안전지대 개수를 구하고, 그 중 최댓값을 찾아 반환한다
3. 코드
- 복습 코드 → 함수, 지역변수로 실행시간 줄이기
import sys from collections import deque input = sys.stdin.readline def bfs(i, j, heights, visited, N, rain): dr = [1, -1, 0, 0] dc = [0, 0, 1, -1] visited[i][j] = True queue = deque() queue.append((i,j)) while queue: r, c = queue.popleft() for i in range(4): nr = r + dr[i] nc = c + dc[i] if 0 <= nr < N and 0 <= nc < N and not visited[nr][nc] and heights[nr][nc] > rain: visited[nr][nc] = True queue.append((nr,nc)) def solution(): N = int(input()) heights = [] Max_height = 0 for _ in range(N): row = list(map(int, input().split())) heights.append(row) Max_height = max(Max_height, max(row)) safe_zone = [] for rain in range(1,Max_height): visited = [ [False for _ in range(N)] for _ in range(N) ] zones = 0 for i in range(N): for j in range(N): if not visited[i][j] and heights[i][j] > rain: bfs(i,j, heights, visited, N, rain) zones += 1 safe_zone.append(zones) if not safe_zone: print(1) else: print(max(safe_zone)) return solution()
- BFS
from collections import deque n = int(input()) graph = [ [] for _ in range(n)] MAX = 0 for i in range(n): graph[i] = list( map( int, input().split()) ) MAX = max( max(graph[i]), MAX ) dx = [ -1, 1, 0, 0 ] dy = [ 0, 0, -1, 1 ] def bfs(x,y,h): queue = deque() queue.append((x,y)) visited[x][y] = 1 while queue: x_, y_ = queue.popleft() for i in range(4): nx = x_ + dx[i] ny = y_ + dy[i] if 0 <= nx < n and 0 <= ny < n and not visited[nx][ny] and graph[nx][ny] > h: queue.append( (nx, ny) ) visited[nx][ny] = 1 result = 0 for i in range(MAX): count = 0 visited = [ [0] * n for _ in range(n) ] for j in range(n): for k in range(n): if graph[j][k] > i and visited[j][k] == 0: bfs(j, k, i) count += 1 result = max(result, count) print(result)
+α
- DFS
import sys sys.setrecursionlimit(100000) n = int(input()) graph = [ [] for _ in range(n)] MAX = 0 for i in range(n): graph[i] = list( map ( int, input().split() ) ) MAX = max( max(graph[i]), MAX ) dx = [ -1, 1, 0, 0 ] dy = [ 0, 0, -1, 1 ] def dfs(x,y,h): visited[x][y] = 1 for i in range(4): nx = x + dx[i] ny = y + dy[i] if 0 <= nx < n and 0 <= ny < n and not visited[nx][ny] and graph[nx][ny] > h: dfs(nx,ny,h) result = 0 for i in range(MAX): count = 0 visited = [ [0] * n for _ in range(n) ] for j in range(n): for k in range(n): if graph[j][k] > i and visited[j][k] == 0: dfs(j, k, i) count += 1 result = max(result, count) print(result)

