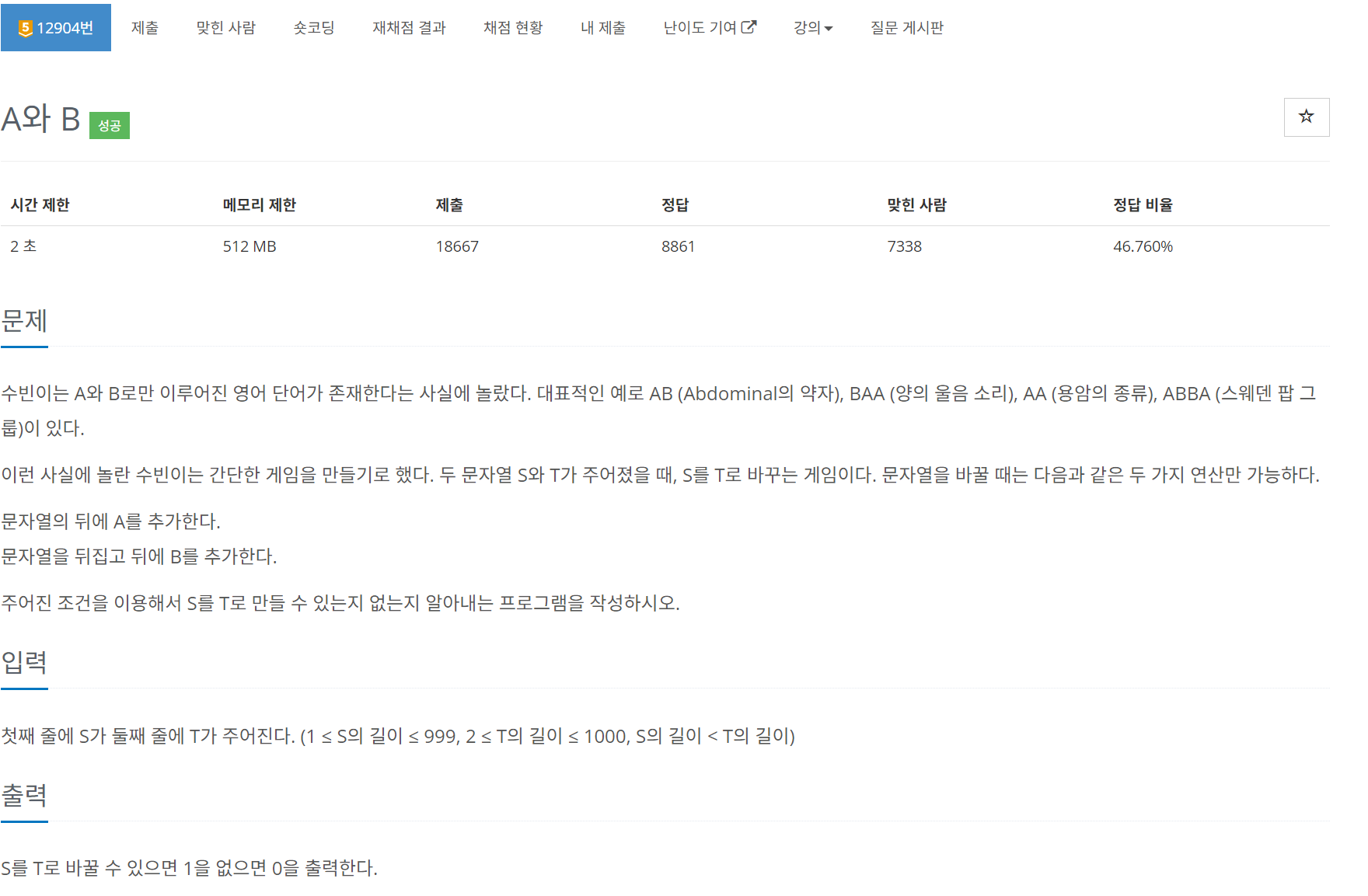
맨 처음에는 백트래킹 방식을 통해 해결법을 생각했다. 하지만 문제를 풀다보니 백트래킹을 이용할려면 특정 조건에 맞지 않으면 return 시킴으로서 효율이 증가하는데 해당 문제는 내세울 조건이 없었다.

문제를 풀다보니 결국 완전 탐색 방식으로 풀게되었고 오답이 나왔다. 답을 찾아보니 S->T로 간다는 생각을 버리고 이미 정답인 T에서 주어진 두 조건에 알맞은 조건을 제외 시키는 방식으로 풀이하면 되는 문제였다.

오답

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;
string s, t;
int flag = 0;


void backtracking(string _s, string _t) {
	if (_s == _t) {
		cout << 1;
		flag = 1;
		return;
	}
	else if(_s.size() < _t.size())
	{
		//문자열의 뒤에 A를 추가한다.
		//문자열을 뒤집고 뒤에 B를 추가
		backtracking(_s + "A", _t);
		reverse(_s.begin(), _s.end());
		backtracking( _s+"B", _t);
	}

	return;
}

int main() {
	ios_base::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	cin >> s >> t;

	//문자열의 뒤에 A를 추가한다.
	//문자열을 뒤집고 뒤에 B를 추가한다.
	//문자열을 빼는건 없음, 같은 동작을 연속으로 해도됨, 그냥 백트래킹 하면 될거같은데? 반복은 s가 t 크기가 될 때까지 -> 빼는게 없으니까

	backtracking(s, t);

	if (flag == 0) {
		cout << 0;
	}

	return 0;
}

정답

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;
string s, t;

int main() {
	ios_base::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	cin >> s >> t;

	int t_index = t.size() - 1;

	while (s.size() < t.size()) {
		if (t[t_index] == 'A') {
			t.pop_back();
		}
		else {
			t.pop_back();
			reverse(t.begin(), t.end());
		}
		t_index -= 1;
	}

	if (s == t) {
		cout << 1;
	}
	else {
		cout << 0;
	}

	return 0;
}