[프로그래머스 / Level 1] 체육복

김나쁜 Kimbad·2022년 8월 17일

코딩테스트

목록 보기

10/22

🚩 문제

문제설명

점심시간에 도둑이 들어, 일부 학생이 체육복을 도난당했습니다. 다행히 여벌 체육복이 있는 학생이 이들에게 체육복을 빌려주려 합니다. 학생들의 번호는 체격 순으로 매겨져 있어, 바로 앞번호의 학생이나 바로 뒷번호의 학생에게만 체육복을 빌려줄 수 있습니다. 예를 들어, 4번 학생은 3번 학생이나 5번 학생에게만 체육복을 빌려줄 수 있습니다. 체육복이 없으면 수업을 들을 수 없기 때문에 체육복을 적절히 빌려 최대한 많은 학생이 체육수업을 들어야 합니다.

전체 학생의 수 n, 체육복을 도난당한 학생들의 번호가 담긴 배열 lost, 여벌의 체육복을 가져온 학생들의 번호가 담긴 배열 reserve가 매개변수로 주어질 때, 체육수업을 들을 수 있는 학생의 최댓값을 return 하도록 solution 함수를 작성해주세요.

제한사항

전체 학생의 수는 2명 이상 30명 이하입니다.

체육복을 도난당한 학생의 수는 1명 이상 n명 이하이고 중복되는 번호는 없습니다.

여벌의 체육복을 가져온 학생의 수는 1명 이상 n명 이하이고 중복되는 번호는 없습니다.

여벌 체육복이 있는 학생만 다른 학생에게 체육복을 빌려줄 수 있습니다.

여벌 체육복을 가져온 학생이 체육복을 도난당했을 수 있습니다. 이때 이 학생은 체육복을 하나만 도난당했다고 가정하며, 남은 체육복이 하나이기에 다른 학생에게는 체육복을 빌려줄 수 없습니다.

입출력 예

n lost reserve return
5 [2, 4] [1, 3, 5] 5
5 [2, 4] [3] 4
3 [3] [1] 2

출처: 프로그래머스 코딩 테스트 연습, https://school.programmers.co.kr/learn/challenges

n	lost	reserve	return
5	[2, 4]	[1, 3, 5]	5
5	[2, 4]	[3]	4
3	[3]	[1]	2

🌌 생각

카테고리가 탐욕법(Greedy)라고 되어있어서 문제 낸 곳의 이름인 줄 알았는데,
알고보니 알고리즘 이름이었다.
(n-잃어버린 사람 수)+(체육복 수 - 잃어버린 사람 수) 하면 되는거 아닌가?

📝 코드 작성

import java.util.*;

class Solution {
    public int solution(int n, int[] lost, int[] reserve) {
        int borrow = reserve.length;
        int lostStudent = lost.length;
        int answer = 0;
        
        for (int i=0; i<lost.length; i++) {
            for (int j=0; j<reserve.length; j++) {
                //여벌 체육복 가져온 학생이 도난당했을 경우
                if (lost[i] == reserve[j]) {
                    borrow--;
                    lostStudent -= 1;
                }
            }
        }
        
        if (lostStudent < borrow) {
            borrow = lostStudent;
        }
        
        answer = n+(borrow-lostStudent);
        return answer;
    }
}

n 총 학생 수
borrow 빌려 줄 수 있는 체육복의 갯수(reserve.length)
lostStudent 잃어버린 학생 수(lost.length)
answer 체육 수업을 들을 수 있는 학생의 수(체육복이 있는 학생 수)

여벌 체육복을 가져온 학생이 자기 체육복을 도난 당했을 경우는
자기 자신한테 빌려주는 개념이므로 lostStudent-1, borrow-1

만약 빌려줄 수 있는 체육복이 잃어버린 학생 수보다 많다면
존재하지 않는 학생에게 체육복을 빌려주는 꼴이 되므로 둘의 갯수를 맞춰준다

총 학생 수 + (빌려줄 수 있는 체육복의 갯수 - 잃어버린 학생 수)를 return

라고 생각했는데 채점 시 20케이스 중 6케이스 정도가 안풀려서 한참을 씨름했다.
문제를 다시 읽어보니,

자기 앞번호나 뒷번호의 학생에게만 체육복을 빌려줄 수 있다

항목의 문제 인 것 같았다.
결국 처음부터 다시 풀었다.

import java.util.*;

class Solution {
    public int solution(int n, int[] lost, int[] reserve) {
        int answer = 0;
        int lostStudent = lost.length;
        int count = 0;
        
        Arrays.sort(lost);
        Arrays.sort(reserve);
        
        for (int i=0; i<reserve.length; i++) {
            for (int j=0; j<lost.length; j++) {
                if (reserve[i] == lost[j]) { // 여분 가진 학생이 도난 당한 경우
                    System.out.println(reserve[i]+"번 학생이 자기 체육복으로 사용합니다.");
                    reserve[i] = -1;
                    lost[j] = -1;
                    lostStudent--;
                }
                if (reserve[i]-1 == lost[j]) { // 앞번호 도난
                    System.out.println(reserve[i]+"번 학생이 "+lost[j]+"번 학생에게 빌려줍니다.");
                    reserve[i] = -1;
                    lost[j] = -1;
                    lostStudent--;
                    count++;
                } else if (reserve[i]+1 == lost[j]) { // 뒷번호 도난
                    System.out.println(reserve[i]+"번 학생이 "+lost[j]+"번 학생에게 빌려줍니다.");
                    reserve[i] = -1;
                    lost[j] = -1;
                    lostStudent--;
                    count++;
                }
            }
        }
        answer = n-lostStudent;
        return answer;
    }
}

앞 번호나 뒷 번호에만 빌려줄 수 있으므로 둘을 대조하기 위해
lost와 reserve를 먼저 정렬을 시켜준다.
그리고 이중 for문 돌리면서 빌려준 학생 번호와 잃어버린 학생 번호를 -1로 만들어
서로를 조건 검사에서 벗어나게 만들면 되지 않을까? 라는 생각으로 만들었다.

이번엔 채점시 2개 케이스에서만 계속 에러가 나서, 무슨 문제인지 또 한참을 고민했다.

❌ 에러 케이스

n = 3
lost = {1,2}
reserve = {2,3}
위의 케이스는
1. 여분이 있는 2번이 1번에게 빌려줌
2. 여분이 있는 3번이 2번에게 빌려줌
따라서 답이 3이 되어버린다. 현실에서는 충분히 가능한 경우다. 하지만,

여분이 있으나 도난 당한 학생은 자신의 여분을 사용한다는 조건이 있으므로
위의 케이스에서 2번은 여분 체육복을 자신의 체육복으로 사용한다. 따라서,
도난 학생 번호 = {1}
여분 학생 번호 = {3}
이 되기 때문에 서로가 앞,뒤번호가 아니므로 대여해줄 수가 없게 된다.

그렇다면 여분 학생 = 도난 학생일 경우만 먼저 처리를 해버리면 되지 않나?

import java.util.*;

class Solution {
    public int solution(int n, int[] lost, int[] reserve) {
        int answer = 0;
        int lostStudent = lost.length;
        int count = 0;
        
        Arrays.sort(lost);
        Arrays.sort(reserve);
        
        for (int i=0; i<reserve.length; i++) {
            for (int j=0; j<lost.length; j++) {
                if (reserve[i] == lost[j]) { // 여분 가진 학생이 도난 당한 경우
                    System.out.println(reserve[i]+"번 학생이 자기 체육복으로 사용합니다.");
                    reserve[i] = -1;
                    lost[j] = -1;
                    lostStudent--;
                }
            }
        }
        
        for (int i=0; i<reserve.length; i++) {
            for (int j=0; j<lost.length; j++) {
                if (reserve[i]-1 == lost[j]) { // 앞번호 도난
                    System.out.println(reserve[i]+"번 학생이 "+lost[j]+"번 학생에게 빌려줍니다.");
                    reserve[i] = -1;
                    lost[j] = -1;
                    lostStudent--;
                    count++;
                } else if (reserve[i]+1 == lost[j]) { // 뒷번호 도난
                    System.out.println(reserve[i]+"번 학생이 "+lost[j]+"번 학생에게 빌려줍니다.");
                    reserve[i] = -1;
                    lost[j] = -1;
                    lostStudent--;
                    count++;
                }
            }
        }
        
        
                
        answer = n-lostStudent;
        return answer;
    }
}

이걸로 채점을 누르니 통과가 되어버렸다.
하지만 내가봐도 난잡하고 만족스럽지 않은 코드다.

✔️ 다른 사람의 코드

class Solution {
    public int solution(int n, int[] lost, int[] reserve) {
        int[] people = new int[n];
        int answer = n;

        for (int l : lost) 
            people[l-1]--;
        for (int r : reserve) 
            people[r-1]++;

        for (int i = 0; i < people.length; i++) {
            if(people[i] == -1) {
                if(i-1>=0 && people[i-1] == 1) {
                    people[i]++;
                    people[i-1]--;
                }else if(i+1< people.length && people[i+1] == 1) {
                    people[i]++;
                    people[i+1]--;
                }else 
                    answer--;
            }
        }
        return answer;
    }
}

최다 추천을 받은 섹시한 솔루션.
훨씬 간결하고, 속도도 빠르다. 내건 정렬 2번에, 2중 for문을 2번 사용하니
속도가 잘 나올래야 잘 나올 수가 없다.

위 코드의 속도

내가 쓴 허접코드의 속도

시간복잡도를 고려했을때 빵점이나 다름 없는 코드다.
더 많이 생각해볼 것.

🧾 욕심쟁이 알고리즘(Greedy Algorithm)

그리디 알고리즘(욕심쟁이 알고리즘, Greedy Algorithm)이란 "매 선택에서 지금 이 순간 당장 최적인 답을 선택하여 적합한 결과를 도출하자"라는 모토를 가지는 알고리즘 설계 기법이다.

예를 들어 5개의 도시를 모두 한번씩만 거쳐서 여행하는 경로 중 기름값을 아끼기 위해 가능하면 짧은 경로를 이용하고 싶다고 가정하자. 이 문제를 해결하기 위해 몇가지 전략을 사용할 수 있다. 가능한 120가지의 조합을 모두 살펴봐서 그중 가장 짧은 경로를 선택하는 것도 하나의 전략이 될 것이다. 그러한 다양한 방법 중, 그리디 알고리즘을 사용한다는 것은 "지금 내가 있는 도시에서 고를 수 있는 도로 중 가장 짧은 도로를 선택한다"라는 방법이 될 수 있다.

단, 그리디 알고리즘을 사용하면 매 선택이 그 순간에 대해서는 최적이지만 그걸 종합적으로 봤을 땐 최적이라는 보장은 절대 없다는 것을 명심해야 한다. 위의 예시에서 매 순간 최적을 따라가면 1-1-1-100라는 순서로 가는데, 중간에 1-1-10-10으로 움직이는 것이 전체적으로 더 짧은 길이 될 수 있으니 말이다.

그리디 알고리즘을 한마디로 설명한다면 그 유명한 마시멜로 실험에 비유할 수 있겠다. 그리디 알고리즘을 사용한다는 것은 지금 당장 눈 앞에 있는 마시멜로를 먹는 것이다. 하지만 이 방법을 사용하는 것은 "기다렸다가 2개를 먹는다"라는 최적해를 보장해주지 못한다.
그리디 알고리즘은 부분의 최적해들의 집합이 곧 전체 문제의 해답이 될 때 사용할 수 있다. 위 서술 같은 경우는 그리디 알고리즘으로 해결 할 수 없는 문제에 그리디 알고리즘을 적용한 경우니 당연히 최적해를 보장해주지 못한다.

어떤 경우에 잘 동작하는가?

그리디 알고리즘은
탐욕 선택 속성(greedy choice property)
최적 부분 구조(optimal substructure)
특성을 가지는 문제들을 해결하는 데 강점이 있다. 즉, 한번의 선택이 다음 선택에는 전혀 무관한 값이어야 하며 매 순간의 최적해가 문제에 대한 최적해여야 한다는 의미이다.

최적 부문 구조

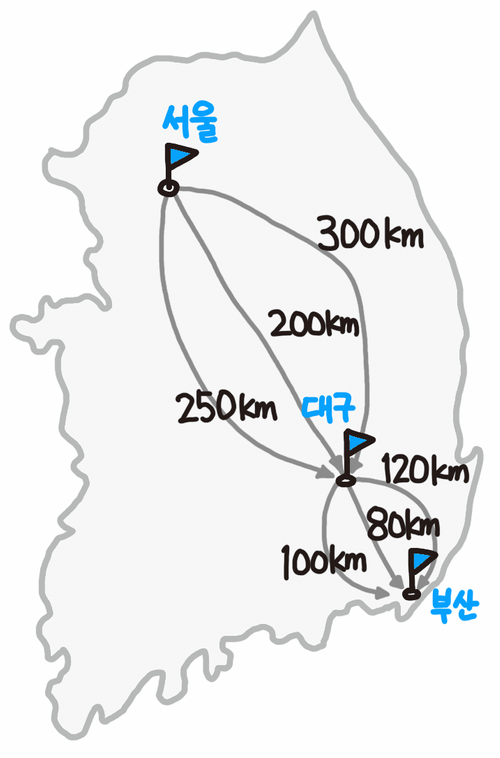
최적 부분 구조를 좀 더 살펴보면 그림과 같이 설명할 수 있다. 서울에서 대구를 거쳐 부산까지 가는 최단 경로를 찾는다고 가정해보자. 그림에서 보듯이, 서울에서 대구까지 가는 경로는 3가지가 있으며, 부산까지도 마찬가지로 3가지 경로가 있다. 서울에서 부산까지 가는 최단 경로는 200km + 80km = 280km이다. 이 경로는 서울에서 대구까지 가는 최단 경로(200km)와 대구에서 부산까지 가는 최단 경로(80km)로 구성된다. 즉 서울에서 대구를 거쳐 부산까지 가는 최단 경로는 각각의 부분 문제인 1)서울에서 대구까지 가는 최단 경로 문제와 2)대구에서 부산까지 가는 최단 경로 문제의 해결 방법의 합이다. 따라서 문제의 최적 해결 방법은 부분 문제에 대한 최적 해결 방법으로 구성된다. 이러한 구조를 최적 부분 구조라 한다.