🟠 구간 합(python): Prefix Sum

구간 합은 합 배열을 이용하여 시간 복잡도를 더 줄이기 위해 사용되는 특수한 목적의 알고리즘이다.

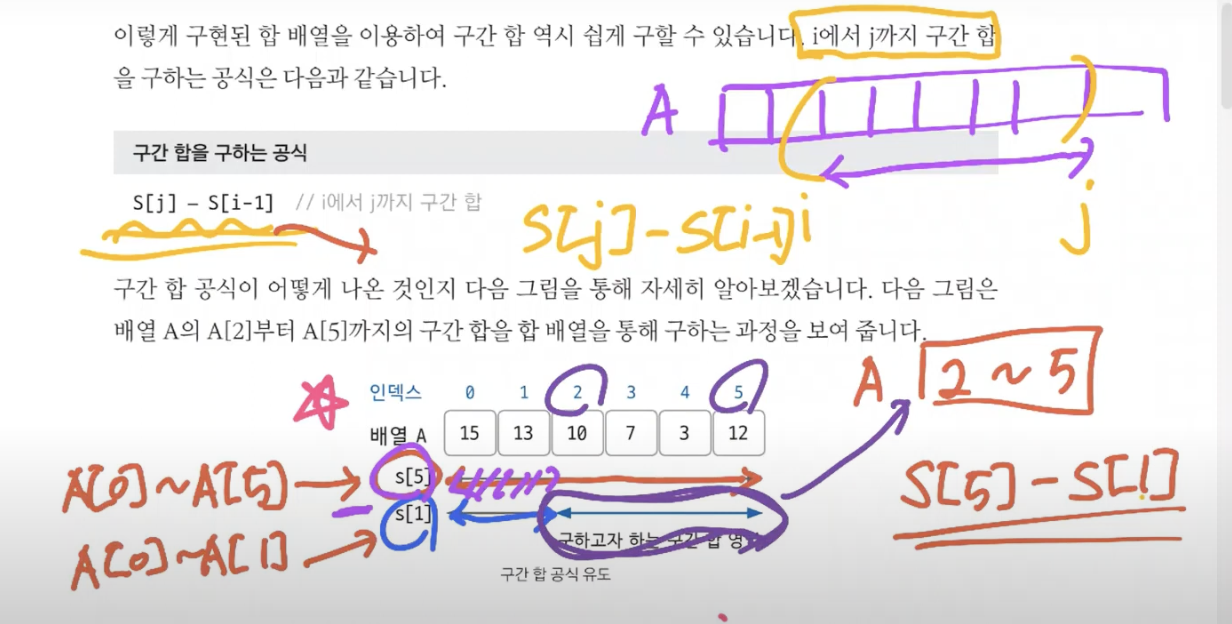
합 배열 S를 만드는 공식

S[i] = S[i-1] + A[i]

구간 합을 구하는 공식

S[j] - S[i-1]

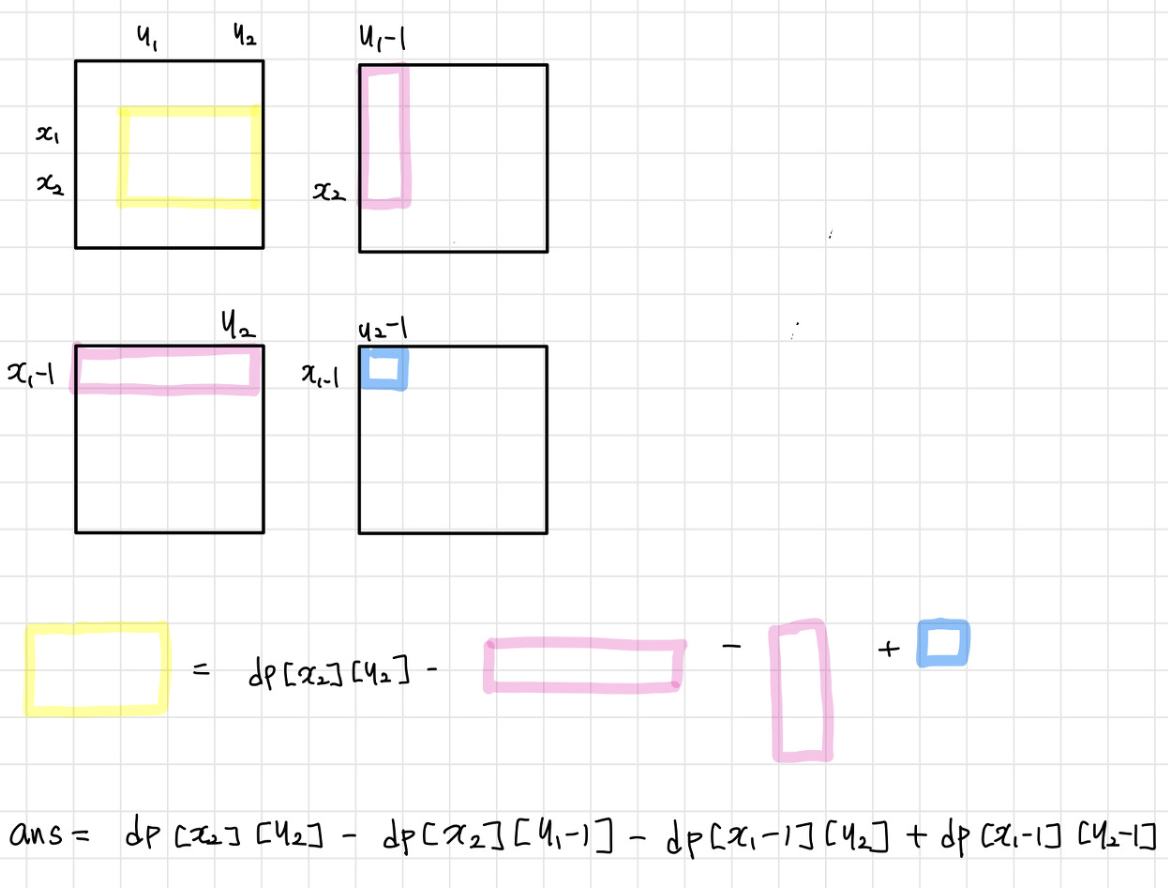
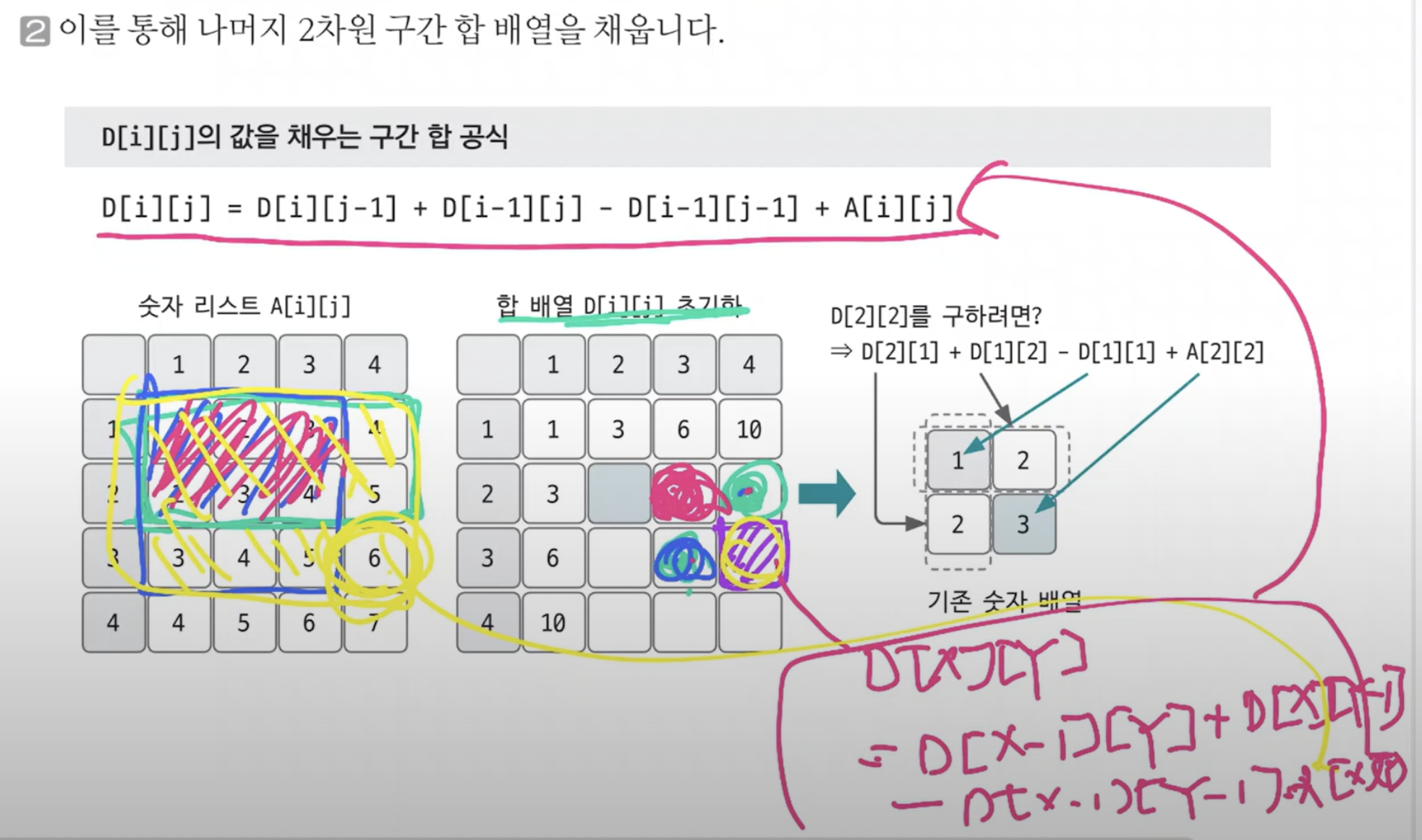
2차원 구간 합 배열 D[X][Y]정의

🦊 [문제] 구간 합 구하기 5

백준 11660번

🐙[문제 풀이]

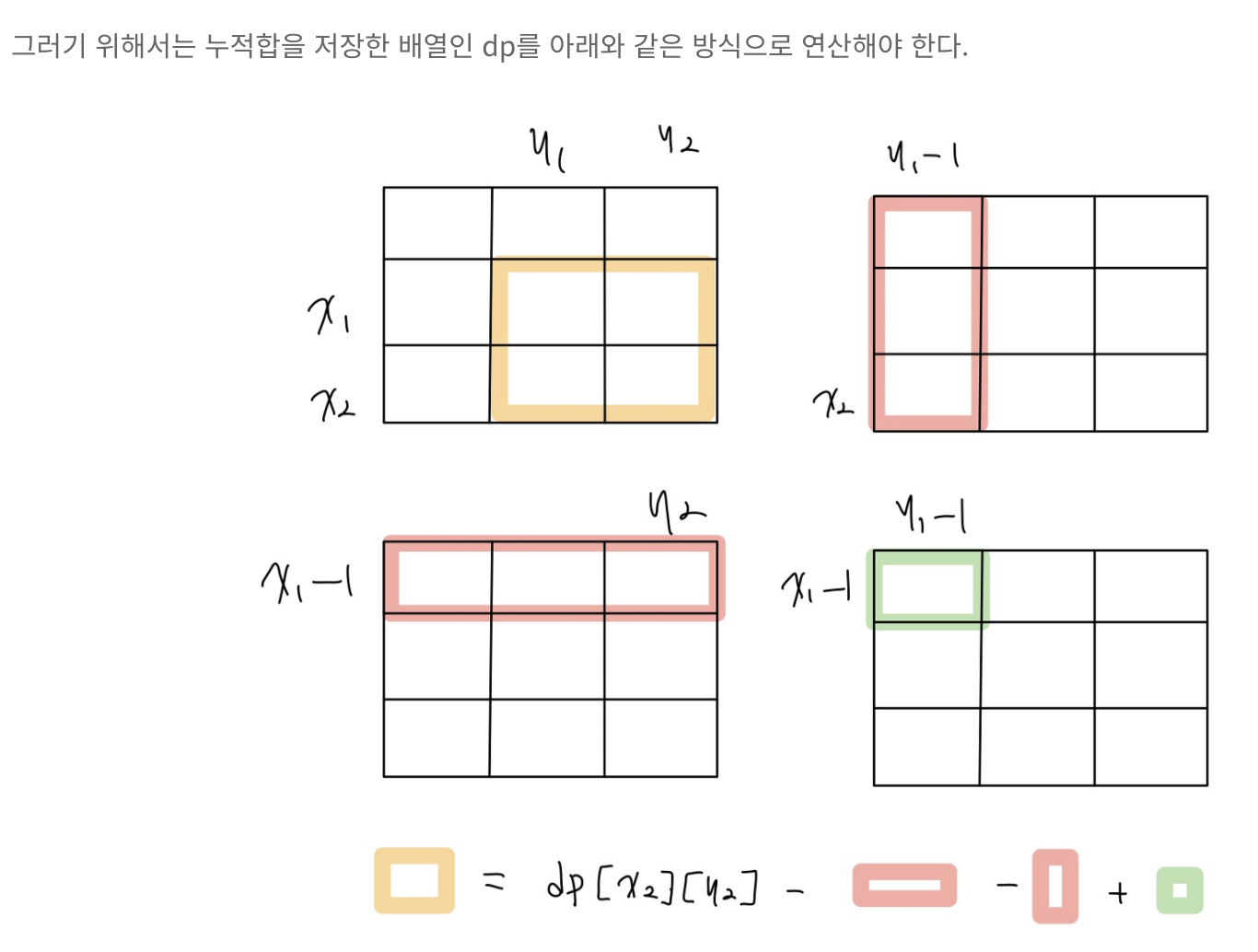
정답 풀이1)

import sys 
input = sys.stdin.readline

# 정답 풀이 
n, m = map(int, input().split())

A = [[0] * (n+1)]

D = [[0] * (n+1) for _ in range (n+1)]

# 누적합 dp 계산(보텀업)
for i in range(n):
  A_row = [0] + [int(x) for x in input().split()]
  A.append(A_row)

# 원하는 구간 계산 
for i in range (1, n+1) :
  for j in range(1, n+1):
    D[i][j] = D[i][j-1] + D[i-1][j] - D[i-1][j-1] + A[i][j]

for _ in range(m):
  x1, y1, x2, y2 = map(int, input().split())
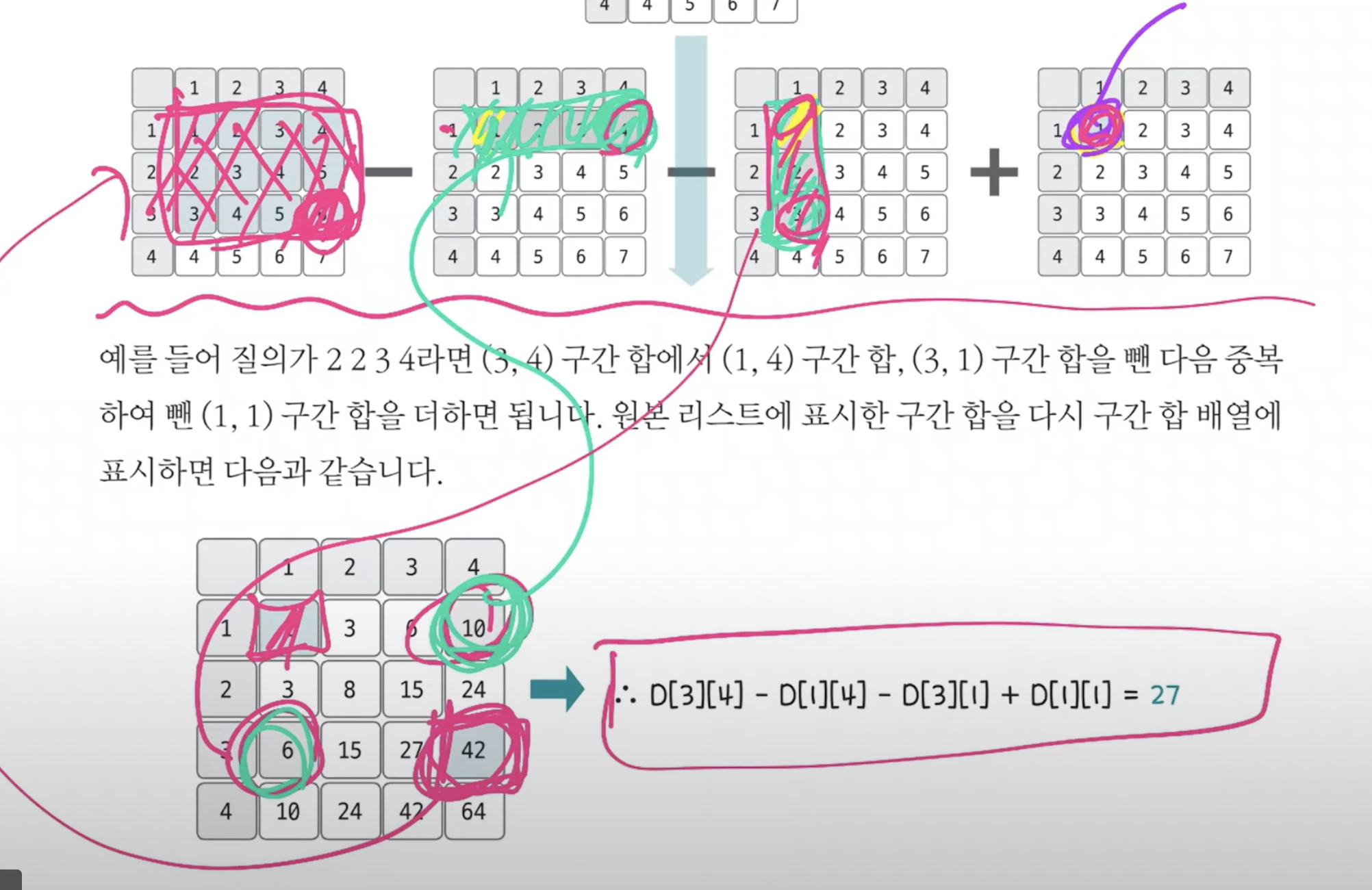
  result = D[x2][y2] - D[x1-1][y2] - D[x2][y1-1] + D[x1-1][y1-1]
  print(result)

정답 풀이2)

import sys 
input = sys.stdin.readline

# 정답 풀이 
n, m = map(int, input().split())

A = [[0] * (n+1)]

D = [[0] * (n+1) for _ in range (n+1)]


for i in range(n):
  A_row = [0] + [int(x) for x in input().split()]
  A.append(A_row)


for i in range (n+1) :
  D[i][1] = D[i-1][i] + A[i][1]
  D[1][j] = D[1][j-1] + A[1][j]

  
for i in range(2, n+1):
  for j in range(2, n+1):
    D[i][j] = D[i][j-1] + D[i-1][j] - D[i-1][j-1] + A[i][j]

for _ in range(m):
  x1, y1, x2, y2 = map(int, input().split())
  result = D[x2][y2] - D[x1-1][y2] - D[x2][y1-1] + D[x1-1][y1-1]
  print(result)

정답 풀이3)

from sys import stdin


n, m = map(int, stdin.readline().split())

numbers = [[0] * (n + 1)]

for _ in range(n):
    nums = [0] + [int(x) for x in stdin.readline().split()]
    numbers.append(nums)

# prefix sum 행렬 만들기

# 1. 행 별로 더하기
for i in range(1, n + 1):
    for j in range(1, n):
        numbers[i][j + 1] += numbers[i][j]

# 2. 열 별로 더하기
for j in range(1, n + 1):
    for i in range(1, n):
        numbers[i + 1][j] += numbers[i][j]

for _ in range(m):
    x1, y1, x2, y2 = map(int, stdin.readline().split())
    # (x1, y1)에서 (x2, y2)까지의 합
    # p[x2][y2] - p[x1 - 1][y2] - p[x2][y1 - 1] + p[x1 - 1][y1 - 1]
    print(numbers[x2][y2] - numbers[x1 - 1][y2] - numbers[x2][y1 - 1] + numbers[x1 - 1][y1 - 1])