문제

링크

풀이

이 문제는 수학 문제라고 생각한다. 규칙을 찾고, 수식을 도출하면 문제를 쉽게 풀 수 있다. 위 문제에서 3개의 기준을 잡고 규칙을 찾아야한다.

1. 면이 하나만 보이는 경우

2. 면이 2개가 보이는 경우

3. 면이 3개가 보이는 경우

N x N x N인 정육면체에서 면이 보이는 경우를 3가지로 나눌 수 있다. (위처럼 오직 3가지 경우밖에 없다!)

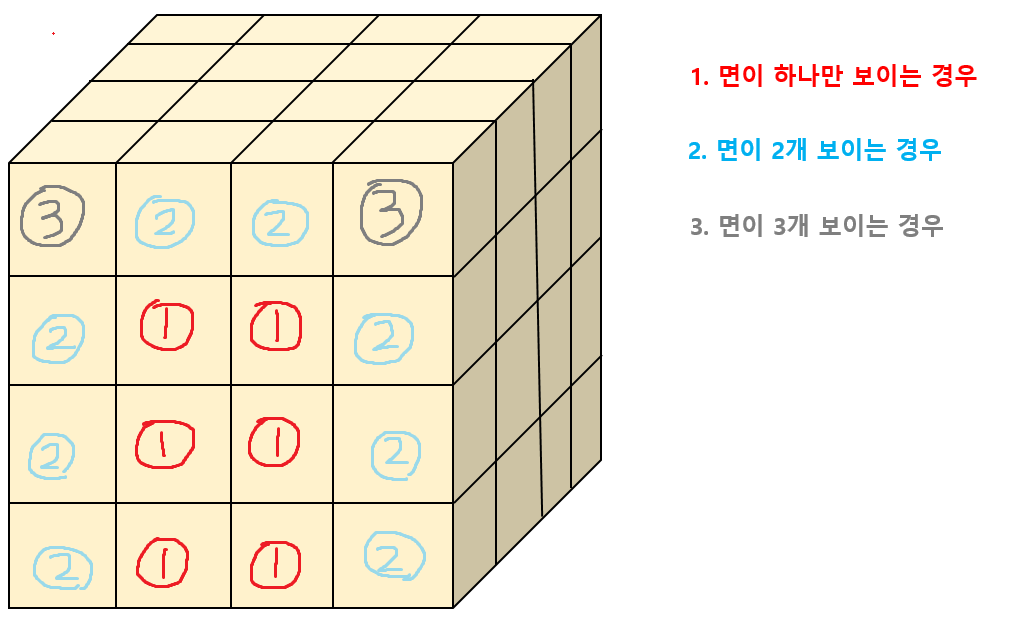
그림을 보면 이해가 훨씬 쉬울 것이다. 이제 규칙을 찾아보자.

N = 1 일 때 --> 1 ~ 5면 다 보임 (바닥에 있는 밑면 하나 빼고 다 보임)
N = 2 일 때 --> 1개 면 0개 / 2개 면 4개 / 3개 면 4개
N = 3 일 때 --> 1개 면 9(1+8)개 / 2개 면 12(4+8)개 / 3개 면 4개
N = 4 일 때 --> 1개 면 28(4+24)개 / 2개 면 20(8+12)개 / 3개 면 4개
...

N이 1일 때만 예외이며, 위 규칙을 통해 식을 도출할 수 있다. 먼저 면이 3개가 보이는 경우는 N값 (단, N > 1)에 상관없이 모두 4개라는 것을 알 수 있다.

1. 면이 하나만 보이는 경우 : 4(N - 1)(N - 2) + (N - 2)²

2. 면이 2개가 보이는 경우 : 4(N - 1) + 4(N - 2)

3. 면이 3개가 보이는 경우 : 4

위 식을 도출하는 과정은 아래와 같다.

면이 하나만 보이는 경우

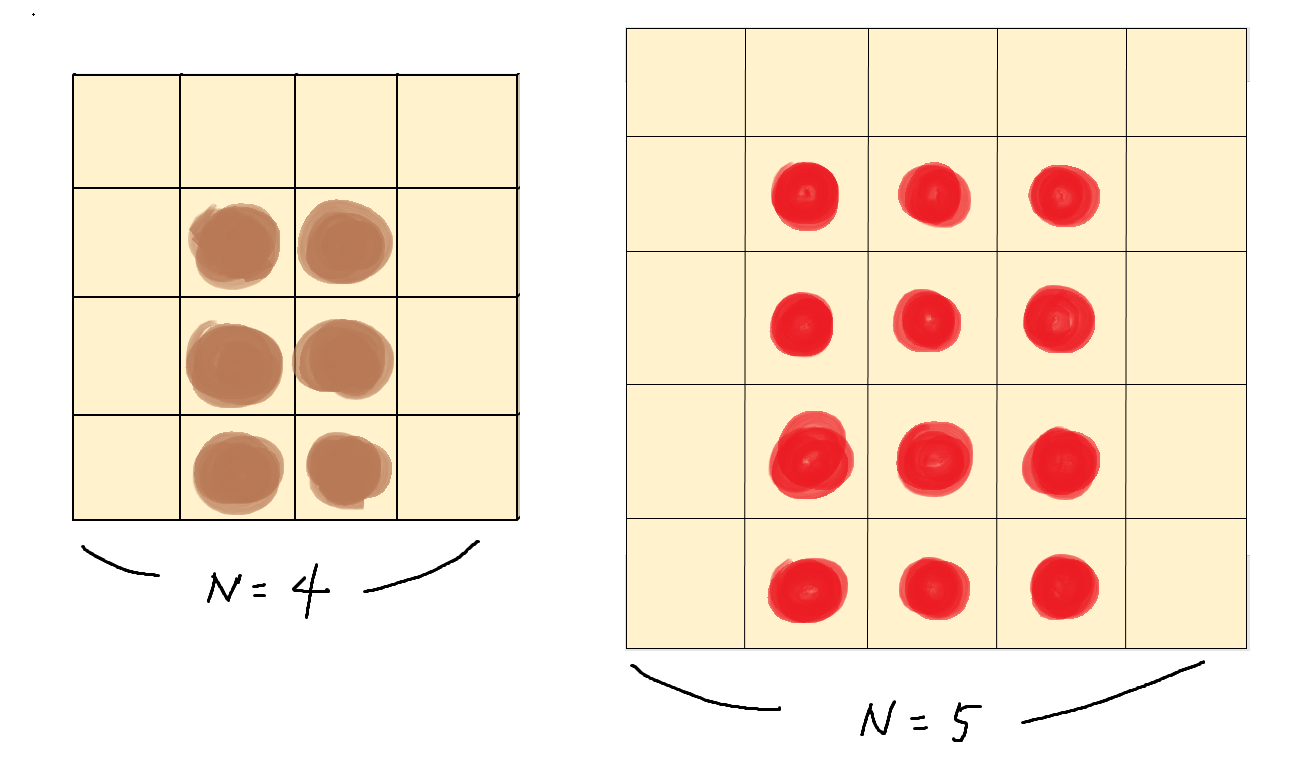
그림은 정육면체를 앞 쪽에서 바라본 모습이다. 색칠한 부분이 면이 하나만 보이는 경우이다. 면이 하나만 보이는 경우, 면의 개수가 (N - 1)(N - 2)개 라는 것을 알 수 있다. 그리고 이러한 면이 총 4개 이므로 4(N - 1)(N - 2)라는 것을 알 수 있다.

마지막으로 정육면체를 위에서 바라봤을 때 면이 하나만 보이는 경우를 구해야한다. 위 그림처럼 직접 그려보게 되면 (N - 2)²개 라는 것을 알 수 있다. 따라서 최종적으로 4(N - 1)(N - 2) + (N - 2)² 식이 도출된다!

면이 2개 보이는 경우

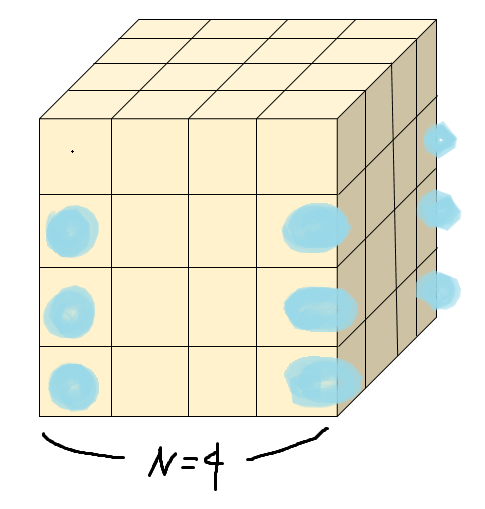
그림에서 색찰한 부분이 면이 2개 보이는 경우이다. 정육면체의 기둥쪽에 면이 2개 보이는 경우가 위치하는 것을 알 수 있다. 한 쪽 기둥만 보자. 면이 2개 보이는 경우, 면의 개수가 (N - 1)개 라는 것을 알 수 있다. 기둥은 총 4개가 있으므로 4(N - 1)라는 것을 알 수 있다.

마찬가지로 정육면체를 위에서 바라봤을 때 면이 2개 보이는 경우를 구해야한다. N이 5, 6, ...일 때를 직접 그려보면 (N - 2)개의 면이 4개의 묶음이라는 것을 알 수 있고, 4(N - 2)라는 것을 알 수 있다. 따라서 최종적으로 4(N - 1) + 4(N - 2) 식이 도출된다!

※ 이후에는 전개도를 통해 [A-F] [B-E] [C-D]가 서로 마주본다는 것을 유의해야한다. 합의 최솟값을 구해야하기 때문에 [A-F 중 최솟값] [B-E 중 최솟값] [C-D 중 최솟값]을 구해야한다.

코드

import sys

input = sys.stdin.readline
N = int(input())
dice = list(map(int, input().split()))
temp = []
ans = 0

if N == 1:
    temp = sorted(dice)
    for i in range(len(temp) - 1):
        ans += temp[i]

else:
    # [A-F 중 최솟값] [B-E 중 최솟값] [C-D 중 최솟값] 구한 후 배열에 저장
    temp.append(min(dice[0], dice[5]))
    temp.append(min(dice[1], dice[4]))
    temp.append(min(dice[2], dice[3]))
    temp.sort()     # 최솟값을 구하기 위해서 오름차순 정렬

    # 보이는 면의 개수에 따른 최솟값 계산 (위 temp 리스트를 정렬한 이유)
    one = temp[0]
    two = temp[0] + temp[1]
    three = temp[0] + temp[1] + temp[2]

    face1 = (4 * (N - 1) * (N - 2)) + ((N - 2) ** 2)
    face2 = 4 * (N - 1) + 4 * (N - 2)

    ans += (one * face1) + (two * face2) + (three * 4)

print(ans)