문제

링크

풀이

각 집중국은 센서의 수신 가능 영역을 조절할 수 있고, 집중국의 수신 가능 영역은 고속도로 상에서 연결된 구간으로 나타나게 된다. 센서가 적어도 하나의 집중국과 통신이 가능해야 한다. 즉, 센서와 집중국이 통신하지 않는 경우는 없다는 것이다. 예제를 통해 설명하려 한다.

(Ex) N:6 / K:2 / 1 6 9 3 6 7
6개의 센서 / 2개의 집중국 / 6개의 센서의 좌표이다.

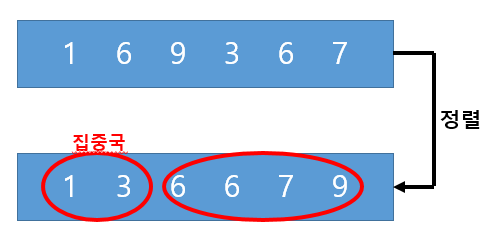
2개의 집중국을 위 그림처럼 세우게 되면 집중국의 수신 가능 영역의 길이의 합의 최솟값을 구할 수 있다. 따라서 답은 (3-1) + (9-6) = 5이다.

처음에는 N개의 센서를 K개로 그룹핑하는 모든 경우의 수를 구하고, 모든 경우에 대한 집중국의 수신 가능 영역의 길이의 합을 계산한 후 최솟값을 구하려 하였다. 중복된 센서가 있어 경우의 수를 처리하기 힘들 것 같았고, 시간초과가 발생할 것 같다고 예상하여 다른 방법으로 풀었다. 아래 그림을 보자.

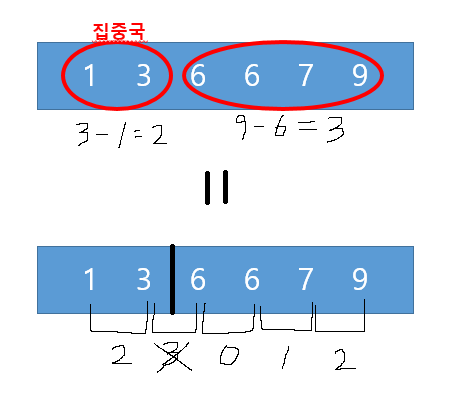
(3-1) + (9-6) = 5인 위의 정답과 2 + 0 + 1 + 2 = 5인 밑의 정답과 같다. 밑의 정답을 보면 각 차이를 계산해주었다. 그 차이는 2, 3, 0, 1, 2 이다. 우리는 2개의 집중국을 세워야하므로 센서를 2개로 그룹핑하게 된다. 수신 가능 영역의 길이의 합이 최소가 되도록 해야하기 때문에 각 차이값들 중 제일 큰 값 3을 제외하고 나머지 차이값들을 더해주게 되면 최솟값을 구할 수 있게된다. 이러한 로직을 이해한다면 문제를 쉽게 풀 수 있다! 아래에 로직을 정리하였다.

1. N개의 센서를 정렬한다. (고속도로에 일직선으로 센서를 설치한다고 생각하면 된다.)

2. 각 원소들의 차이를 순서대로 구한다. (길이가 (N-1)인 배열에 저장하게 된다.)

3. 각 원소들의 차이를 오름차순으로 정렬한다.

4. (K-1)개의 원소를 삭제한다. 단, 가장 값이 큰 원소부터 지워야한다. (최솟값을 구해야하기 때문이다.)

5. 삭제되지 않은 각 원소들의 차이를 모두 더한다. (이들의 합이 정답이다.)

※ 예외처리를 해야한다!! 집중국의 개수가 센서의 개수보다 크거나 같으면 정답이 0이 된다.

코드

import sys

input = sys.stdin.readline
N = int(input())
K = int(input())
sensor = list(map(int, input().split()))
sensor.sort()

if K >= N:
    print(0)

else:
    focus = []
    for i in range(N - 1):
        focus.append(abs(sensor[i] - sensor[i + 1]))
    focus.sort()

    for _ in range(K - 1):
        focus.pop()

    print(sum(focus))